数学１
今回はデータの散らばりについての続きになります。データの散らばりの度合いを知るための数量として、四分位数や箱ひげ図を学習しました。
四分位数や箱ひげ図だけがデータの散らばりの度合いを知るものではありません。ここでも新しい数量を学習します。
いくつか公式が出てきますが、この単元も頻出です。しっかり使えるようにしておきましょう。
この単元で学習すること
「データの散らばり（その２）」では以下のような事柄を学習します。
これらもデータの散らばりの度合いを知るためのものです。新しい用語がたくさん出てきますが、１つずつ丁寧に確認していきましょう。
偏差
ある変量についてのデータの値が以下のように定義されているとします。
変量とデータの各値
変量 x についてのデータの値が、n 個の値x1 , x2 ,⋯⋯, xnであるとする。
このように変量とデータの各値が定義されているとき、平均値は以下のように表されます。
データの平均値
x1 , x2 ,⋯⋯, xnの平均値を ¯x とすると¯x=1n(x1+x2+⋯⋯+xn)または¯x=1nn∑k=1xk（数列の知識があれば、文字式ではこちらの方が扱いやすい）
このとき、変量ｘのｎ個の各値と平均値との差をそれぞれ平均値からの偏差と言います。
変量の各値と偏差
\begin{align*}
\begin{array}{c|c|c|c|c}
\scriptsize{\text{値}} & x_{\scriptsize{1}} & x_{\scriptsize{2}} & \cdots \cdots & x_{\scriptsize{n}} \\
\hline
\scriptsize{\text{偏差}} & x_{\scriptsize{1}} \ – \overline{x} & x_{\scriptsize{2}} \ – \overline{x} & \cdots \cdots & x_{\scriptsize{n}} \ – \overline{x}
\end{array}
\end{align*}
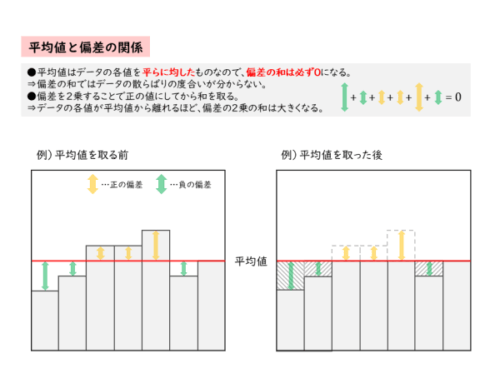
偏差は各値が平均値からどれだけ離れているかを表す値なので、この偏差を用いるとデータの散らばりの度合いを知ることができます。しかし、偏差には正の値と負の値があるので、このまま偏差の和を取ってしまうと、平均値と偏差の関係からおかしなことになってしまいます。
平均値と偏差の関係 平均値は、各値を平らに均したときの値です。平均するとき、各値の過不足を互いに補うようにして平らに均します。このときの過不足が偏差に相当します。ですから、偏差の和を求めると必ず０になります。このままだと、データの散らばりの度合いを知ることに利用できないので、少し工夫します。
分散
偏差をそのまま用いるのではなく、各偏差をそれぞれ２乗し、すべて正の値にしてから利用します。この偏差の２乗の平均値を分散と言います。分散は以下のように表されます。
分散
\begin{align*}
&\text{分散を $s^{\scriptsize{2}}$ とすると、} \\[ 5pt ]
&\quad s^{\scriptsize{2}} = \frac{1}{n} \left\{ ( x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + (x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots \cdots + (x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\} \\[ 7pt ]
&\text{または} \\[ 5pt ]
&\quad s^{\scriptsize{2}} = \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } (x_{\scriptsize{k}} \ – \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&\scriptsize{\text{（数列の知識があれば、文字式ではこちらの方が扱いやすい）}}
\end{align*}
分散は、データの各値が平均値から離れるほど大きな値を取るようになるので、データの散らばりの度合いを表す量として用いられます。
また、分散の式において、右辺を展開して整理すると、以下の式を導出することができます。
分散を表す別式
\begin{align*}
s^{\scriptsize{2}} &= \frac{1}{n} \left\{ ( x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + (x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots \cdots + (x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\} \\[ 7pt ]
&= \frac{1}{n} \left\{ ( {x_{\scriptsize{1}}}^{\scriptsize{2}} + {x_{\scriptsize{2}}}^{\scriptsize{2}} + \cdots + {x_{\scriptsize{n}}}^{\tiny{2}} ) \ – 2x_{\scriptsize{1}}\overline{x} \ – 2x_{\scriptsize{2}}\overline{x} \ – \cdots \ – 2x_{\scriptsize{n}}\overline{x} + ( \overline{x} )^{\scriptsize{2}} + ( \overline{x} )^{\scriptsize{2}} + \cdots + ( \overline{x} )^{\scriptsize{2}} \right\} \\[ 7pt ]
&= \frac{1}{n} \left\{ ( {x_{\scriptsize{1}}}^{\scriptsize{2}} + {x_{\scriptsize{2}}}^{\scriptsize{2}} + \cdots + {x_{\scriptsize{n}}}^{\scriptsize{2}} ) \ – 2\overline{x} ( x_{\scriptsize{1}} + x_{\scriptsize{2}} + \cdots + x_{\scriptsize{n}} ) + n ( \overline{x} )^{\scriptsize{2}} \right\} \\[ 7pt ]
&= \frac{1}{n} ( {x_{\scriptsize{1}}}^{\scriptsize{2}} + {x_{\scriptsize{2}}}^{\scriptsize{2}} + \cdots + {x_{\scriptsize{n}}}^{\scriptsize{2}} ) \ – 2\overline{x} \cdot \frac{1}{n} ( x_{\scriptsize{1}} + x_{\scriptsize{2}} + \cdots + x_{\scriptsize{n}} ) + ( \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \overline{x^{\scriptsize{2}}} \ – 2\overline{x} \cdot \overline{x} + ( \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \overline{x^{\scriptsize{2}}} \ – ( \overline{x} )^{\scriptsize{2}} \\[ 10pt ]
\therefore \ s^{\scriptsize{2}} &= \overline{x^{\scriptsize{2}}} \ – ( \overline{x} )^{\scriptsize{2}}
\end{align*}
この式を導出するときに注意したいのは、各値の２乗の平均値です。平均値の２乗とは別物です。
各値の２乗の平均値
\begin{align*}
&\text{$x^{\scriptsize{2}}$ のデータを} \\[ 5pt ]
&\quad {x_{\scriptsize{1}}}^{\scriptsize{2}} \ , \ {x_{\scriptsize{2}}}^{\scriptsize{2}} \ , \ \cdots \cdots \ , \ {x_{\scriptsize{n}}}^{\scriptsize{2}} \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad \overline{x^{\scriptsize{2}}} = \frac{1}{n} ( {x_{\scriptsize{1}}}^{\scriptsize{2}} + {x_{\scriptsize{2}}}^{\scriptsize{2}} + \cdots + {x_{\scriptsize{n}}}^{\scriptsize{2}} )
\end{align*}
ちなみにシグマ（Σ）を使った式の方でも導出できます。多少は変形が楽になります。
分散を表す別式
\begin{align*}
s^{\scriptsize{2}} &= \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } (x_{\scriptsize{k}} \ – \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } \left\{ {x_{\scriptsize{k}}}^{\scriptsize{2}} \ – 2x_{\scriptsize{k}} \ \overline{x} + ( \overline{x} )^{\scriptsize{2}} \right\} \\[ 7pt ]
&= \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } {x_{\scriptsize{k}}}^{\scriptsize{2}} + \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } ( – 2x_{\scriptsize{k}} \ \overline{x} ) + \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } ( \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } {x_{\scriptsize{k}}}^{\scriptsize{2}} \ -2\overline{x} \cdot \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } x_{\scriptsize{k}} + \frac{1}{n} \cdot n ( \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \overline{x^{\scriptsize{2}}} \ -2\overline{x} \cdot \overline{x} + ( \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
&= \overline{x^{\scriptsize{2}}} \ – ( \overline{x} )^{\scriptsize{2}} \\[ 10pt ]
\therefore \ s^{\scriptsize{2}} &= \overline{x^{\scriptsize{2}}} \ – ( \overline{x} )^{\scriptsize{2}}
\end{align*}
実際の問題では、文字が変わる可能性があるので、ことばで覚えておくと良いでしょう。
分散
分散
＝偏差の２乗の平均値
＝各値の２乗の平均値 \overline{x^{\scriptsize{2}}} － 各値の平均値の２乗 \left( \overline{x} \right)^{\scriptsize{2}}
分散は平均値と同じくらい利用頻度が高いので、確実に覚えましょう。
分散の式の使い分け
分散を表す式が２つあることが分かりました。もちろん、どちらでも分散を求めることはできますが、平均値によって計算のやりやすさが変わります。
平均値が簡単な整数のときならば、どちらの式を用いても計算のやりやすさにそれほど差がありません。しかし、平均値が複雑な値（たとえば分数）になれば、別式の方を用いた方が計算がいくらかましになります。
定義の式だけを覚えて、それだけを運用することも１つの手ですが、やはり状況に応じて使い分けできるようにしておきたいところです。
分散の式の使い分けの目安
- 平均値が簡単な整数のとき：どちらの式でもOK
- 平均値が複雑な値（たとえば分数）：定義の式より別式で
標準偏差
偏差の和が０になってしまうことから、偏差の２乗の平均値を分散としました。
しかし、分散の単位が、変量の測定単位の２乗となってしまいます。そこで、変量の測定単位を揃えるために、分散の正の平方根を用いて、散らばりの度合いを表すこともあります。
この分散の正の平方根を標準偏差と言います。
変量、分散、標準偏差の単位
たとえば、測定単位がｍのとき、分散の単位はｍ2、標準偏差の単位はｍ
標準偏差
標準偏差は、分散 s^{\tiny{2}} の正の平方根であるので
\begin{align*}
&\quad s = \sqrt{\frac{1}{n} \left\{( x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + (x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots \cdots + (x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\}} \\[ 10pt ]
&\text{または} \\[ 5pt ]
&\quad s = \sqrt{\overline{x^{\scriptsize{2}}} \ – ( \overline{x} )^{\scriptsize{2}}} \\[ 10pt ]
&\text{$x_{\scriptsize{1}} \ , \ x_{\scriptsize{2}} \ , \cdots \cdots , \ x_{\scriptsize{n}}$ ：変量 $x$ におけるデータの値} \\[ 7pt ]
&\text{$\overline{x}$ ：変量 $x$ におけるデータの平均値} \\[ 7pt ]
&\text{$x_{\scriptsize{1}} \ – \overline{x} \ , \ x_{\scriptsize{2}} \ – \overline{x} \ , \cdots \cdots , \ x_{\scriptsize{n}} \ – \overline{x}$ ：偏差} \\[ 7pt ]
&\text{$\overline{x^{\scriptsize{2}}}$ ：変量 $x^{\scriptsize{2}}$ におけるデータの平均値}
\end{align*} 標準偏差は、分散と同じくデータの散らばりの度合いを表す量として用いられます。
標準偏差と分散の大きな違いは、分散の正の平方根が標準偏差になるので、単位が測定単位と同じかそうでないかになります。
分散や標準偏差の式は少し複雑ですが、演習をこなしてしっかり覚えましょう。
表を上手に利用しよう
分散や標準偏差を求める計算では、データの大きさが大きくなるほど項の数が増えるので、計算ミスをしやすくなります。計算ミスを防ぐ方法の１つは、表にまとめることです。
表にまとめるとき、偏差や偏差の２乗などの項目を必要に応じて書き加え、そこに値を記入していきます。
表の一例
変量 x の値が 5 \ , \ 7 \ , \ 4 \ , \ 3 \ , \ 6 の平均値、分散、標準偏差を求める。
\begin{align*}
&\quad \overline{x} = \frac{5+7+4+3+6}{5} = \frac{25}{5} = 5 \\[ 7pt ]
&\text{表にまとめると} \\[ 5pt ]
&\begin{array}{c|c|c}
x_{\scriptsize{k}} & x_{\scriptsize{k}} \ – \overline{x} & (x_{\scriptsize{k}} \ – \overline{x} )^{\scriptsize{2}} \\[ 7pt ]
\hline
5 & 0 & 0 \\[ 5pt ]
\hline
7 & 2 & 4 \\[ 5pt ]
\hline
4 & -1 & 1 \\[ 5pt ]
\hline
3 & -2 & 4 \\[ 5pt ]
\hline
6 & 1 & 1 \\[ 5pt ]
\hline
\scriptsize{\text{計}} & 0 & 10
\end{array} \\[ 10pt ]
&\text{表より} \\[ 5pt ]
&\quad s^{\scriptsize{2}} = \frac{10}{5} = 2 \\[ 7pt ]
&\quad s = \sqrt{2} \fallingdotseq 1.4 \\[ 7pt ]
&\text{よって、平均値 $5$、分散 $2$、標準偏差 $1.4$}
\end{align*} 列の最後に和（計）の欄を作っておくと、公式に値を代入して求めるよりも手早く分散を求めることができます。また、偏差の和が０になることも確認できるので、計算ミスに気づくこともできます。
分散だけなく、標準偏差などの値も求めることが多くなります。ですから、表にまとめておくのは２度手間を省けてとても便利です。
データの分析では、データをいかに手際よく扱えるかが大切なので、表を上手に利用した方が些細な計算ミスを減らせます。
偏差や偏差の２乗などの情報も表にまとめて、計算ミスを減らそう。
次は、分散や標準偏差などを扱った問題を実際に解いてみましょう。
