データの分析｜データの散らばりについて その１

07/11/2021数学１

今回はデータの散らばりについて学習しましょう。平均値や中央値などの代表値は、データの特徴を知るのに役立ちます。しかし、データの全体像を把握するのにはあまり向いていません。データの全体像を把握するには、データがどのくらい散らばっているかといった、データの散らばりの度合いを調べる必要があります。

ここでは、どのような値がデータの全体像を把握するのに向いているのかを学習します。データの特徴だけでなく、データの散らばりも調べることで、データをより詳しく分析することができるようになります。

この単元で学習すること

「データの散らばり（その１）」では以下のような事柄を学習します。

データを扱うために色々な用語が定義されているので、１つずつ丁寧に確認していきましょう。

範囲

データの最大値と最小値の差を範囲と言います。範囲が大きければ大きいほど、データが散らばっていると考えることができるので、この範囲だけでもデータの全体像を大まかに把握することができます。

データの値の個数を表す「データの大きさ」と間違えやすいので注意しましょう。

四分位数

データを値の大きさの順に並べたとき、データの個数を４等分する位置にある３つの値のことを四分位数と言います。小さい方から順に、第１四分位数、第２四分位数、第３四分位数と言い、これらを記号でＱ₁，Ｑ₂，Ｑ₃と表します。

四分位数の求め方にはコツがあります。まず、データを値の大きさの順に左から右に並べてから、データを中央値で２等分します。中央値が第２四分位数Ｑ₂になります。

たとえば、データの大きさが７とします。このとき、中央値は４番目の値となり、この値が第２四分位数Ｑ₂です。

また、データを２等分したので、左半分に第２四分位数Ｑ₂以下の値が並ぶ下位のデータができ、そして右半分に第２四分位数Ｑ₂以上の値が並ぶ上位のデータができます。

次に下位と上位のデータにおいて、中央値をそれぞれ求めます。これらが第１四分位数Ｑ₁と第３四分位数Ｑ₃になります。下位と上位のデータをそれぞれ２等分したので、データ全体では４等分したことになります。

データを４つに分けるには、境は３つあれば良いので、四分位数は４つではなく３つです。「四つに分ける位置を示す数」と解釈すれば覚えやすいでしょう。なお、四分位数の定義は他にもあるそうですが、高校数学では上記のように定義されたものを用います。

四分位数の求め方の手順をまとめると以下のようになります。

四分位範囲と四分位偏差

データの散らばりの度合いを表すものとして、範囲の他に四分位範囲や四分位偏差などがあります。

第３四分位数から第１四分位数を引いた値を四分位範囲と言います。先程紹介した「範囲」とは異なるので注意しましょう。一般に、以下のように表されます。

また、四分位範囲を２で割った値を四分位偏差と言います。一般に、以下のように表されます。

先程のデータであれば、四分位範囲と四分位偏差は以下のようになります。

範囲、四分位数、四分位範囲、四分位偏差を用いることで、データの散らばりの度合いを把握したり、他のデータと比較したりすることができます。

箱ひげ図

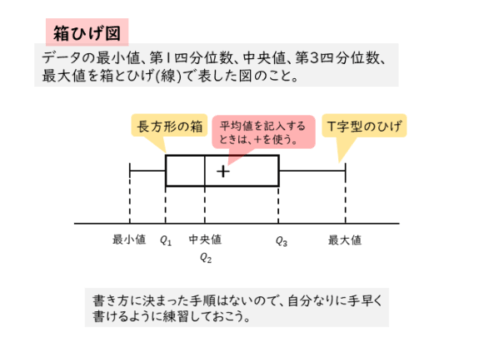
データの最小値、第１四分位数、中央値（第２四分位数）、第３四分位数、最大値を可視化したものを箱ひげ図と言います。名前の通り、長方形の箱とＴ字型の線（ひげ）を用いた図です。

箱ひげ図は、複数のデータ（たとえば年度別や地域別など）の分布を比較するときによく用いられます。複数のデータの箱ひげ図を並べることで、データの散らばりの度合いを比較しやすいのが特徴です。

箱ひげ図は以下のような図になります。長方形の箱とＴ字型の線（ひげ）を使って表します。最小値や第１四分位数など各種の値が、箱ひげ図のどこに対応しているのかをしっかり覚えましょう。

箱ひげ図によっては、データの平均値を記入する場合があります。平均値は、プラス（＋）の記号で表しますが、特に指示がなければ記入しなくても構いません。

実際にデータをもとに箱ひげ図を書くと以下のようになります。

データの大きさが奇数のときと偶数のときとで異なるのは、四分位数の求め方です。

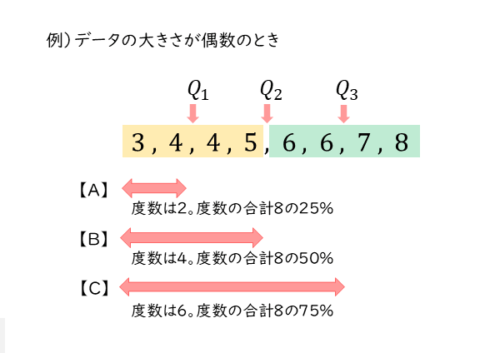
データの大きさが偶数のとき、第１～３四分位数は、四分位数となる位置の前後にある２数の平均値となります。データの大きさが偶数のときは、厳密に言えばデータを４等分する位置に数がないからです。

例２（上図）のように、データの大きさが８のとき、中央値である第２四分位数は４番目と５番目の数５，６の平均値５.５です。

また、下位のデータは１番目から４番目までの数となり、そのときの中央値である第１四分位数は２番目と３番目の数４，４の平均値４です。

さらに、上位のデータは５番目から８番目までの数となり、そのときの中央値である第３四分位数は６番目と７番目の数６，７の平均値６.５です。

箱ひげ図を書く手順は、特に決まっていません。自分なりに書きやすい手順で書きましょう。

箱ひげ図と度数の関係

箱ひげ図を書くこと自体はそれほど難しくありません。難しいのは、箱ひげ図から正しく情報を読み取ることです。

実際、箱ひげ図から読み取れることの正誤を考える問題の方がよく出題されます。他には、新しい値が追加された後の箱ひげ図を予想する問題も出題されます。

これらの問題は、箱ひげ図から正しく情報を読み取れなければ難しい問題です。このような問題に対応するには、自分で箱ひげ図を書いた経験が必要です。

正誤問題で間違えやすいのが、度数の読み取りです。箱ひげ図はデータの散らばりの度合いを見たり、比べたりするものなので、度数は記入されていません。しかし、四分位数の性質を利用すれば、度数を読み取ることができます。

大きさが８のデータを例に四分位数と度数の関係を考えてみましょう。四分位数は以下のようになります。

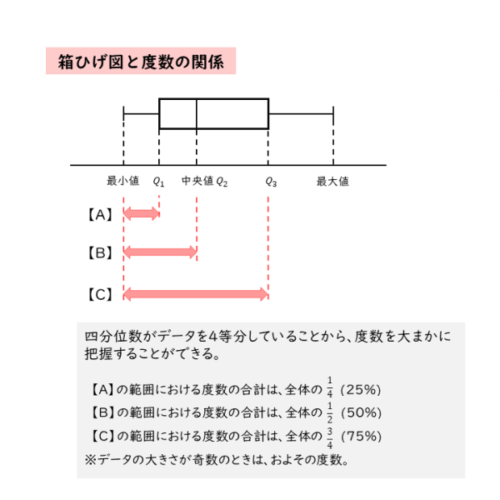
データの大きさが偶数であれば、データが四分位数によってきれいに４等分（２個ずつに分割）されていることが分かります。このことから、特定の範囲にある度数の全体に占める割合が分かります。

この割合を覚えておけば、データの大きさをもとに特定の範囲の度数を求めることができます。

データの大きさが奇数の場合、偶数の場合と異なり、およその度数になるので注意しましょう。箱ひげ図で見ると以下のようになります。

箱ひげ図を見て度数の割合を考えると、簡単に引っ掛かってしまいます。

先程も言ったように、箱ひげ図はデータの散らばりの度合いを見るもので、度数ではなく、データの各値を用いて作成します。ですから、度数が等しい場合であっても、四分位数で分けられた４つの部分の幅が等しくなるとは限りません。

各部分の幅のせいで度数が異なるように感じますが、データで見れば分かるように、度数は四分位数できちんと４等分されています。

これまでに出てきた用語をまとめると、以下のようになります。

次は、四分位数や箱ひげ図などを扱った問題を実際に解いてみましょう。