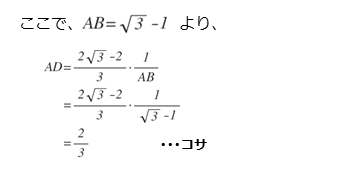数学1・A|2017センター試験・第2問を解いてみよう

今さら、センター試験の過去問を解いても意味がないと思うかもしれません。もちろん、共通テストになったためにセンター試験とは形式の変わる部分が出てきますが、問題のレベルに大きな差があるとは考えられません。
形式に慣れることは難しいかもしれません。しかし、センター試験の過去問から、自分の学力レベルを把握することができるでしょう。入試レベルへの到達度を知ることは、とても大切なことです。
今回は、2017年センター試験数学1・Aの第2問についてです。
2016年と比べても出題の形式や内容がほとんど変わっていないので、過去問を解いていればスムーズに解けたのではないかと思います。
記事の画像が見辛いときはクリックすると拡大できます。
数学1・Aの第2問について
第1問は、数1の「図形と計量」と「データの分析」の単元からの出題でした。各単元の出題内容をまとめると以下のようになります。
図形と計量からの出題内容
- 余弦定理に関する問題
- 正弦定理に関する問題
- 三角形の面積に関する問題
データの分析からの出題内容
- 散布図・ヒストグラム・箱ひげ図の読み取りに関する問題
- 分散・共分散・相関係数などに関する問題
どちらの単元も教科書例題レベルなので、完答したい問題です。
「図形と計量」に関する問題では、一般に、図形を扱うのが原因なのか、教科書例題レベルでも難しく感じます。しかし、本問に関して言えば、比較的解きやすい部類だったので、完答しないと勿体ないレベルです。
また、「データの分析」に関する問題では、分散・共分散・相関係数の値を公式を用いて求める問題ではありませんでした。
どちらかと言うと、分散・共分散・相関係数の公式が使えるかを問う問題です。このような問題は2016年でも出題されており、ほぼ同じ出題内容でした。
もし、完答できなかったとしたら準備不足です。完答できるかどうかは別として、やはり過去問での対策は大切だとよく分かる問題でした。
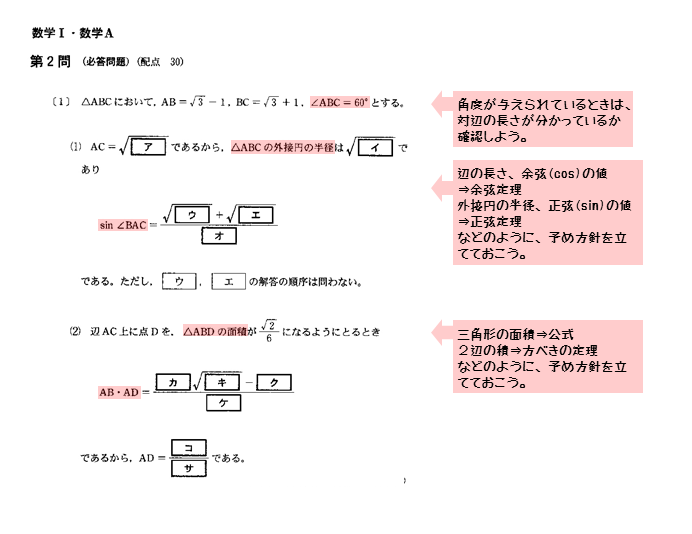
第2問〔1〕について
第2問〔1〕は「図形と計量」に関する問題です。全体を俯瞰してみると、小問(1),(2)の2部構成になっています。
最初に与えられた辺の長さに平方根が混じっています。おそらく問題自体は難しくなく、計算過程でミスを誘発させる意図が感じられる問題です。無駄な計算ミスをしないように注意しましょう。
また、図形の問題なので、作図してイメージを膨らませながら解いていきましょう。辺の長短に注意しながら、できるだけ精度の高い作図が良いでしょう。
作図することで、長さの長短や角度の大きさなど、気付きを得ることがある。
解答欄ア
解答欄アに関する問題は、△ABCの辺ACの長さを求める問題です。
△ABCを作図すると方針がすぐに決まるでしょう。

2辺AB,BCの長さと、2辺がつくる∠ABCの大きさが分かっています。このようなときは迷わず余弦定理を利用します。
余弦定理
公式との対応関係を確認してから値を代入して計算します。このとき、辺の長さが平方根を含む多項式になっているので、乗法公式による展開が必要になります。ミスなく解を導出しましょう。
解答欄アの解答例をまとめると以下のようになります。
余弦定理や正弦定理がどのような条件で使える定理なのかを知っておこう。「2辺と角が与えられている」=「余弦定理で残りの一辺」あるいは「三角形の辺の長さ=余弦定理」くらいの感覚で。
解答欄イ
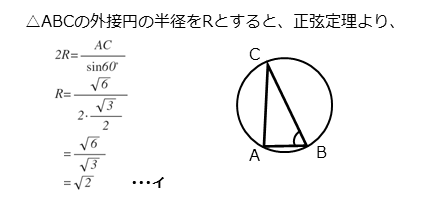
解答欄イに関する問題は、△ABCの外接円の半径を求める問題です。
「外接円の半径」とくれば「正弦定理」です。

角の大きさが分かっているのは∠ABCで、その対辺は辺ACです。辺ACの長さは先ほど求めたので、それを利用します。ただし、辺ACの値が間違っていれば、全滅するので注意しましょう。
正弦定理
公式との対応関係を確認してから値を代入して計算します。
解答欄イの解答例をまとめると以下のようになります。
解答欄ウエオ
解答欄ウエオに関する問題は、sin∠BACの値を求める問題です。
sinは正弦と言うくらいなので、この問題も正弦定理を利用して求めます。

正弦定理
正弦定理の式は4つの値がすべて等しいことを表しています。ですからどれか2つを選んで等式(6通り)を作ることができます。
たとえば、解答欄ウエオの値を求めるために2つを選ぶと以下のような等式を作れます。
正弦定理の式の使い方
これより
\begin{align*} \quad \frac{BC}{\sin \angle BAC} = 2R \end{align*}公式との対応関係を確認してから値を代入して計算します。このとき、sin∠BACについて変形してから値を代入しましょう。
解答欄ウエオの解答例をまとめると以下のようになります。
公式をそのまま使うのではなく、公式を変形してから数を代入した方が計算の負担が少なくなる。計算ミスをしない工夫をしよう。
小問(1)は、余弦定理や正弦定理を利用する基本的な問題でした。すぐに方針が立つので、ミスなく速やかに解きたい問題です。
解答欄カキクケ
小問(2)において、新たに点Dが条件に加わるので、図に追記しておきましょう。
解答欄カキクケに関する問題は、2辺の積AB・ADを求める問題です。
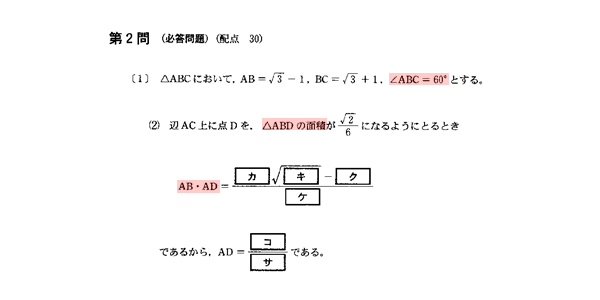
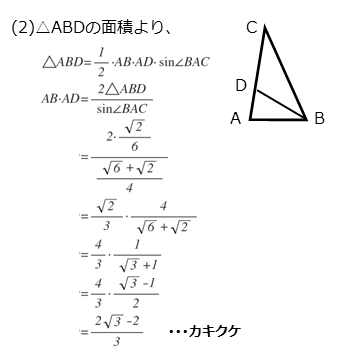
条件で与えられた△ABDの面積を求める式を考えると、2辺の積AB・ADが出てきます。
△ABDのの面積S
2辺の積AB・ADが出てきましたが、∠BADが問題です。
作図していれば、∠BAD=∠BACであることに気付けたでしょう。それに、この関係からsin∠BACの値を利用できることにも気付きます。
アルファベットが異なると、異なる角を示しているような気がするが、そうとは限らない。図を使って解く習慣をつけよう。
面積の公式を2辺の積AB・ADについて変形しておきます。そして、式に対応する値を代入して計算します。
解答欄カキクケの解答例をまとめると以下のようになります。
公式の基本的な使い方だけでなく、公式を変形して使う応用的な使い方もマスターしておこう。公式の暗記で満足しないようにしよう。
解答欄コサ
解答欄コサに関する問題は、2辺の積AB・ADの値を前提にして、辺ADの長さを求める問題です。
先ほどの2辺の積AB・ADの問題と連動していることに注意しましょう。

辺ABの長さと2辺の積AB・ADの値は既に分かっています。
2辺の積AB・ADの値を辺ABの長さで割れば、辺ADの長さを求めることができます。おまけみたいな問題なので、サービス問題だと思って確実に導出しましょう。
辺ADの長さを求める
ADについて変形したあと、ABに値を代入します。
このとき、ABの値は平方根を含む多項式です。分母の有理化が必要になりそうですが、分子に注目すると約分できることに気付きます。式をよく観察して、上手に計算しましょう。
解答欄コサの解答例をまとめると以下のようになります。
第2問〔1〕のポイントと解答例をまとめると以下のようになります。メモ書きなどもあるので、参考になれば幸いです。
次は、第2問〔2〕を解いてみましょう。