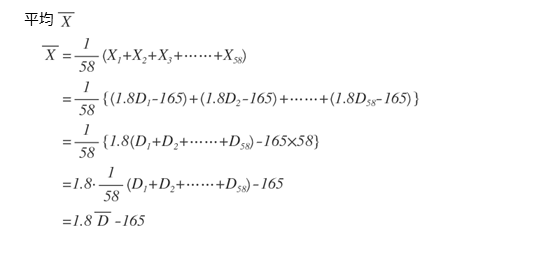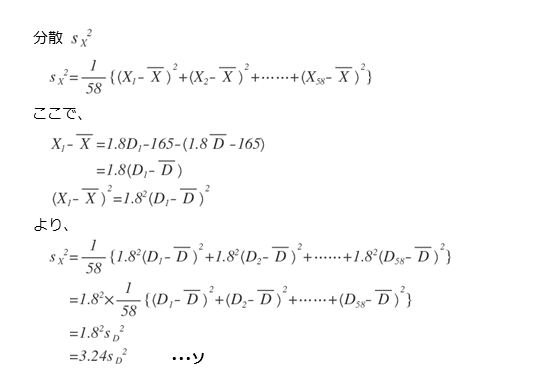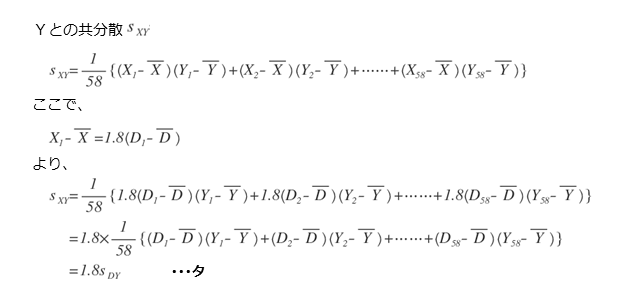数学１・Ａ｜2017センター試験・第２問を解いてみよう
第２問〔２〕について
第２問〔２〕は「データの分析」に関する問題です。
全体の構成は、小問(1)，(2)，(3)の３部構成になっています。出題の順番や扱っている題材は多少変わっていますが、出題内容は例年通りです。
第２問〔２〕の小問(1)について
第２問〔２〕の小問(1)は、散布図に関する問題です。
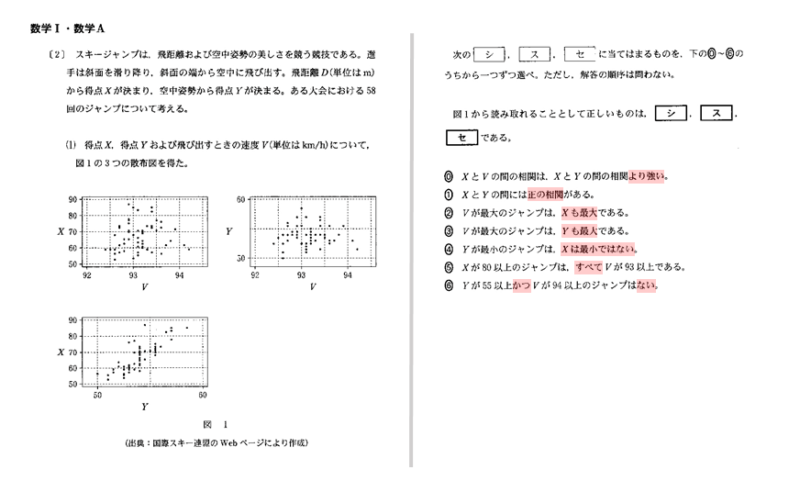
解答欄シスセ
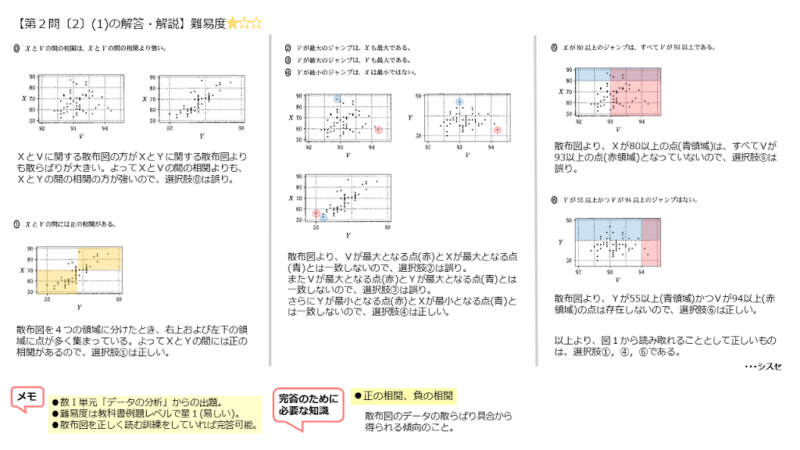
解答欄シスセは、散布図の読み取り、選択肢の内容と吟味する問題です。
選択肢０の吟味
選択肢０：ＸとＶの間の相関は、ＸとＹの間の相関よりも強い。
選択肢０は、散布図における相関の強さに関する説明文です。
散布図はデータの散らばり具合を知ることができる図です。データの散らばり具合を見れば、データの相関の強さも分かります。
散布図の散らばり具合から、ＸとＹの間の相関の方が、ＸとＶの間の相関よりも強いと読み取れます。ですから、ＸとＶの間の相関は、ＸとＹの間の相関よりも弱いと言えるので、選択肢０の内容は誤りと言えます。
データが散らばれば散らばるほど、データ間の相関は弱い。また、データが集まれば集まるほど、データ間の相関は強い。
選択肢１の吟味
選択肢１：ＸとＹの間には正の相関がある。
選択肢１は、散布図における正負の相関についての説明文です。
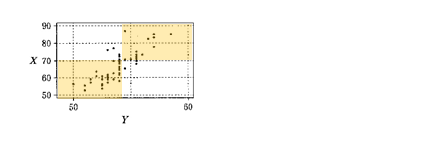
散布図を座標平面のように４つの領域に分けると、反時計回りに右上の領域（Ｉの領域）、左上の領域（IIの領域）、左下の領域（IIIの領域）、右下の領域（IVの領域）ができます。
このように分けたとき、右上の領域（Ｉの領域）と左下の領域（IIIの領域）にデータが集まっていれば「正の相関がある」と言います。
また、左上の領域（IIの領域）と右下の領域（IVの領域）にデータが集まっていれば「負の相関がある」と言います。
散布図からＸとＹの間には正の相関があると読み取れるので、選択肢１の内容は正しいと言えます。
少し乱暴だが、データが右上がりに集まっているときに「正の相関」、右下がりに集まっているときに「負の相関」と覚えておくと良い。
選択肢２，３，４の吟味
選択肢２：Ｖが最大のジャンプは、Ｘも最大である。
選択肢３：Ｖが最大のジャンプは、Ｙも最大である。
選択肢４：Ｙが最小のジャンプは、Ｘは最小ではない。
選択肢２，３，４は、データの最大値や最小値についての説明文です。データの最大値や最小値を散布図から読み取らなければなりません。
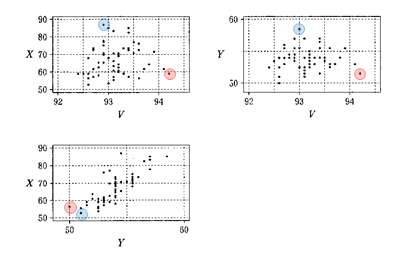
散布図が３つあるので、データに合わせて参照する散布図を変えます。散布図からＶ，Ｘ，Ｙが最大になる点や、Ｘ，Ｙが最小になる点を探します。
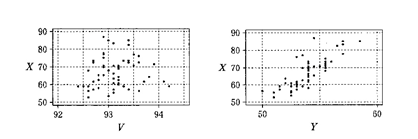
ＶとＸの散布図を参照すると、選択肢２の内容を吟味できます。
散布図からＶが最大になる点とＸが最大になる点とが一致しません。
選択肢３，４についても選択肢２と同じように点を探します。
３つの説明文を吟味すると、この中では選択肢４の内容だけが正しいと言えます。
選択肢５の吟味
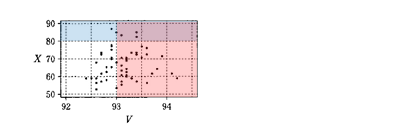
選択肢５：Ｘが８０以上のジャンプは、すべてＶが９３以上である。
選択肢５の吟味です。ＸとＶに関する散布図を参照します。
Ｘが８０以上になる領域（図の青領域）にあるデータが、すべてＶが９３以上になる領域（図の赤領域）に入っているかを調べます。
散布図から、Ｘが８０以上になるデータのうち、Ｖが９３以上になる領域に入っていないデータがあることが読み取れるので、選択肢５の内容は誤りだと言えます。
選択肢６の吟味
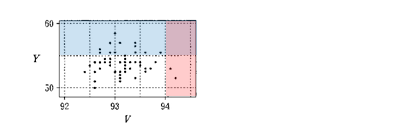
選択肢６：Ｙが５５以上かつＶが９４以上のジャンプはない。
選択肢６の吟味です。ＹとＶに関する散布図を参照します。
Ｙが５５以上になる領域（図の青領域）とＶが９４以上になる領域（図の赤領域）とが重なった領域にデータがあるのかを調べます。
散布図から重なった領域にデータがないと読み取れるので、選択肢６の内容は正しいと言えます。
散布図から読み取ると言っても、選択肢の内容と照らし合わせるだけの簡単な作業です。必要な散布図を選び、手早く吟味しましょう。
第２問〔２〕(1)のポイントと解答例をまとめると以下のようになります。
次は第２問〔２〕の小問(2)を解いてみましょう。
第２問〔２〕の小問(2)について
第２問〔２〕の小問(2)は、分散・共分散・相関係数に関する問題です。
解答欄ソタチ
得点Ｘが飛距離Ｄの１次式で与えられています。これより、Ｘに関する分散・共分散・相関係数は、Ｄに関する分散・共分散・相関係数で表すことができます。
得点Ｘは飛距離Ｄの１次式で表される
Ｄに関する平均・分散・共分散・相関係数をそれぞれ求めておきます。また、ＸとＤについての与式も展開して整理しておきます。
Ｘの平均を求めると、以下のようになります。得点ＸをＤの１次式に置換して整理すると、Ｘの平均はＤの平均で表すことができます。
また、Ｘの分散も同じ要領でＤの分散で表すことができます。これが解答欄ソの答えになります。
さらに、ＸとＹの共分散も同様にして、ＤとＹの共分散で表すことができます。これが解答欄タの答えになります。
さいごに、ＸとＹの相関係数をＤとＹの相関係数で表します。これが解答欄チの答えになります。
小問(2)のような問題は、2016年に摂氏と華氏との関係で出題されていました。
過去問で対策していれば解ける問題ですが、公式を暗記しているだけでは時間内に解くのは難しい問題だと思います。公式を使えるレベルかどうかがはっきりする良問だと思います。
ただ、試験中に導出するのは時間的に厳しいので、一度自力で導出した後は性質として覚えておきましょう。
２つのデータについて、一方のデータが他方のデータの一次式で表されるとき、平均や分散などは一般に以下のように表せます。
この性質を利用すれば、かなり時間を短縮することができました。
データが１次式で表されるときの性質を利用する
のとき
Ｘの分散
\begin{align*} \quad {s_X}^{2} = {\left(1.80\right)}^{2} \times {s_D}^{2} \end{align*}ＸとＹの共分散
\begin{align*} \quad s_{XY} = 1.80 \times s_{DY} \end{align*}ＸとＹの相関係数
\begin{align*} \quad r_{XY} = r_{DY} \end{align*}第２問〔２〕(2)のポイントと解答例をまとめると以下のようになります。
第２問〔２〕(2)のポイントと解答例の続きです。
次は、第２問〔２〕の小問(3)を解いてみましょう。
第２問〔２〕の小問(3)について
第２問〔２〕の小問(3)は、ヒストグラムや箱ひげ図に関する問題です。
解答欄ツ
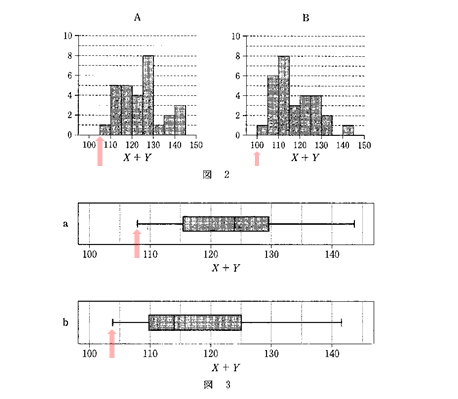
解答欄ツに関する問題は、正しいヒストグラムと箱ひげ図の組み合わせを選ぶ問題です。
ヒントになるのは、文章中にある「１回目のＸ＋Ｙの最小値」です。
１回目のＸ＋Ｙの最小値は１０８．０です。
これをもとにして、ヒストグラムと箱ひげ図の最小値をそれぞれ確認します。
ヒストグラムと箱ひげ図より、Ａとａの組み合わせが正しいことが分かります。
解答欄テ
解答欄テに関する問題は、箱ひげ図（図３）の読み取りに関する問題です。
選択肢の吟味
選択肢０：１回目のＸ＋Ｙの四分位範囲は、２回目のＸ＋Ｙの四分位範囲よりも大きい。
選択肢１：１回目のＸ＋Ｙの中央値は、２回目のＸ＋Ｙの中央値よりも大きい。
選択肢２：１回目のＸ＋Ｙの最大値は、２回目のＸ＋Ｙの最大値よりも小さい。
選択肢３：１回目のＸ＋Ｙの最小値は、２回目のＸ＋Ｙの最小値よりも小さい。
四分位範囲は箱の幅（図の赤矢印）に対応しています。
２回目の方が箱の幅が大きいので、２回目の方が四分位範囲が大きくなります。このことから、選択肢０は誤りと言えます。
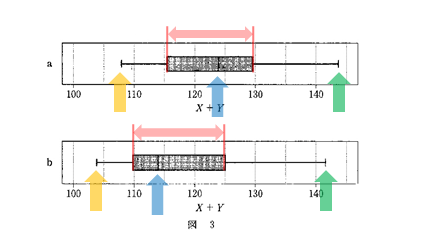
中央値は箱内の縦線（図の青矢印）に対応しています。
この縦線の位置を比べると１回目の方が右側にあるので、１回目の方が中央値が大きくなります。
このことから、選択肢１は正しいと言えます。
最大値はひげ右端の縦線（図の緑矢印）に対応しています。
この縦線の位置を比べると１回目の方が右側にあるので、１回目の方が最大値が大きくなります。
このことから、選択肢２は誤りと言えます。
最小値はひげ左端の縦線（図の黄矢印）に対応しています。
この縦線の位置を比べると２回目の方が左側にあるので、２回目の方が最小値が小さくなります。
このことから、選択肢３は誤りと言えます。
以上の吟味から、正しい選択肢は①となります。
箱ひげ図では、中央値、第１～３四分位数、四分位範囲などとの対応関係が問われる。
第２問〔２〕(3)のポイントと解答例をまとめると以下のようになります。
従来の第２問との比較
第２問は、図形と計量」と「データの分析」に関する問題でした。
「図形と計量」に関する問題は、図形によって難易度が左右されやすく、「データの分析」に関する問題は、数値の取り扱いが煩雑になりがちです。どちらの分野も意外と鬼門になりやすいです。
しかし、今回は「図形と計量」は解きやすく、「データの分析」の分析も例年と比べてほとんど数値を扱うことがありませんでした。
これらを考慮すると、完答するのは決して難しい要求とは言えないレベルの問題だったと思います。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
共通テスト対策として必要なことをすべて備えた理想の予想問題集が完成
単に問題を解くだけでなく、その背景にある考え方や知識まで掘り下げて解説。「分析編」では、過去2回の試行調査（プレテスト）から見えてきた共通テストの出題傾向を詳細に分析するだけでなく、学習法や学習姿勢などの具体的な対策まで説明。本番でそのまま出そうな予想問題と、くわしい解説がセットになった至高の実践型問題集。
もくじ
- 本冊
- 分析編
- 解答・解説編
- 別冊
- 試行調査：２回分（2017年度／2018年度）
- 予想問題：２回分
公式サイトでは、一部の内容を閲覧できます。
KADOKAWAの公式サイト
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
教科書で確認しておきたい知識
- 正弦定理や余弦定理は利用できる条件とセットで覚えておく。
- 公式を変形して使う応用的な使い方をマスターしよう。
- 必ずしも「アルファベットが違う＝角が違う」とは限らない。
- 散布図では、相関の強さや正負の相関が分かる。
- 平均・分散・標準偏差・共分散・相関係数などの公式の暗記だけで満足しない。
- 箱ひげ図と最大値・最小値、第１～３四分位数などとの対応関係を知っておく。