数学1・A|2017センター試験・第5問を解いてみよう

今さら、センター試験の過去問を解いても意味がないと思うかもしれません。もちろん、共通テストになったためにセンター試験とは形式の変わる部分が出てきますが、問題のレベルに大きな差があるとは考えられません。
形式に慣れることは難しいかもしれません。しかし、センター試験の過去問から、自分の学力レベルを把握することができるでしょう。入試レベルへの到達度を知ることは、とても大切なことです。
今回は、2017年センター試験の数学1・Aの第5問についてです。
第5問は「図形の性質」に関する問題です。第2問と同じように、図形の問題では作図が必須です。日頃から作図しながら問題を解いているかで勝負が決まりそうです。
日常的な学習では、個別試験(2次試験)にも対応できるような学習を心掛けましょう。
ここ数年、作図なしでは難易度の高い問題の割合が増えており、作図の重要度が増している。記述のことを考えて作図しようと思えばできる状態にはしておきたい。
記事の画像が見辛いときはクリックすると拡大できます。
数学I・Aの第5問について
第5問は、数Aの「図形の性質」の単元からの出題でした。出題内容をまとめると以下のようになります。
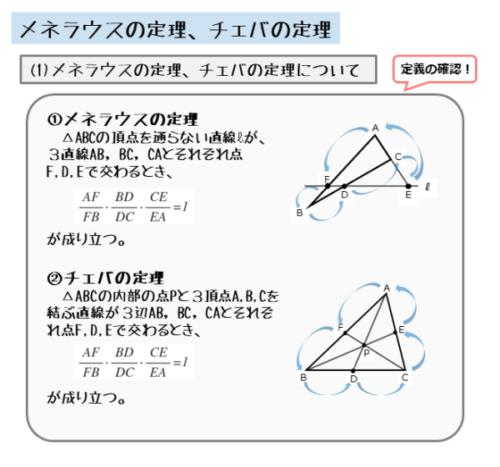
「図形の性質」からの出題内容
- 三角形と円に関する問題
- 三角形の内心に関する問題
- 方べきの定理やメネラウスの定理を利用する問題
図形が複数出てくるので、やはり作図が必要な問題です。そうは言ってもほとんどが教科書例題レベルなので、ぜひ完答を目指したい問題です。
「図形の性質」の単元は、中学校で学習した、三角形・四角形などの図形の性質や、合同・相似など図形どうしの関係についての知識がベースになっています。
色々と定理や公式が出てきますが、それらも中学で学習した内容の延長です。
図形に関する問題なので、何度も言いますが作図することが大切です。作図することによってイメージがより具体的になり、場合によっては様々な気付きを与えてくれます。
図形の性質は図形で理解する。そのための作図。デメリットはないと言っても良いので、日頃から作図を心掛けよう。
第5問をざっと確認してみましょう。
全体を俯瞰してみると、(1),(2)の小問形式になっています。
他の選択問題と比べると格段に易しかったので、図形に対して苦手意識がある人にとってはラッキーな問題だったかもしれません。
なお、必答問題の大問2つを解いた後、第5問へと進むと時間配分が上手くいったのではないかと思います。
第5問(1)について
(1)は、三角形と外接円に関わる問題、そしてメネラウスの定理を扱った問題で構成されています。どちらも特に捻った問題でもなかったので、あっさり解けた人が多かったかもしれません。
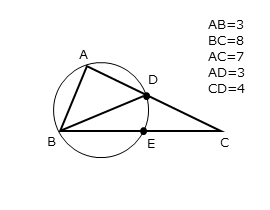
問題文を読みながら正しく作図しましょう。そうしないと、何の外接円か分からなくなってしまうので注意したいところです。今回は△ABCではなく、△ABDの外接円です。
解答欄アイ,ウエ
解答欄アイ,ウエ
条件1
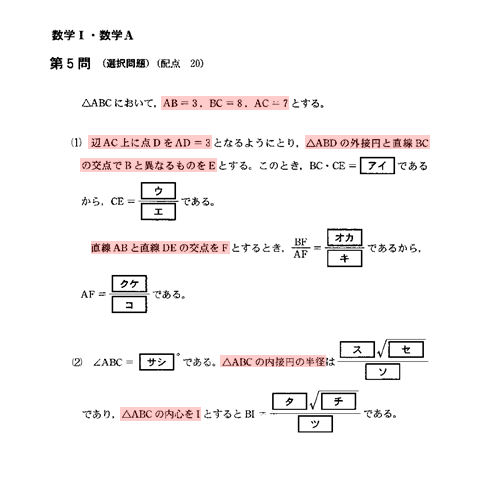
$\triangle {ABC}$ おいて、$AB=3 \ , \ BC=8 \ , \ AC=7$
条件2
辺 $AC$ 上に $AD=3$ となる点 $D$ をとる。
条件3
$\triangle {ABD}$ の外接円と直線 $BC$ の交点で $B$ と異なるものを $E$ とする。
このとき
$BC \cdot CE$ の値(解答欄アイ)
$CE$ の値(解答欄ウエ)
与えられた条件で作図をすると分かります。
さて、作図して色々と分かったところで問題を解いていきます。
解答欄アイに関する問題は、2つの線分BC,CEの長さの積BC・CEを求める問題です。
また、解答欄ウエに関する問題は、 BC・CEの値を利用してCEの値を求める問題です。
2つの線分の積が出てきている時点で「方べきの定理」が候補に挙がります。しかも、外接円まで出てきたので「方べきの定理」で確定です。
方べきの定理を用いて、長さの積BC・CEの値を求めます。
解答欄アイの解答例
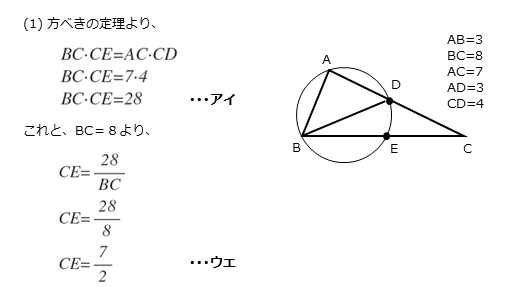
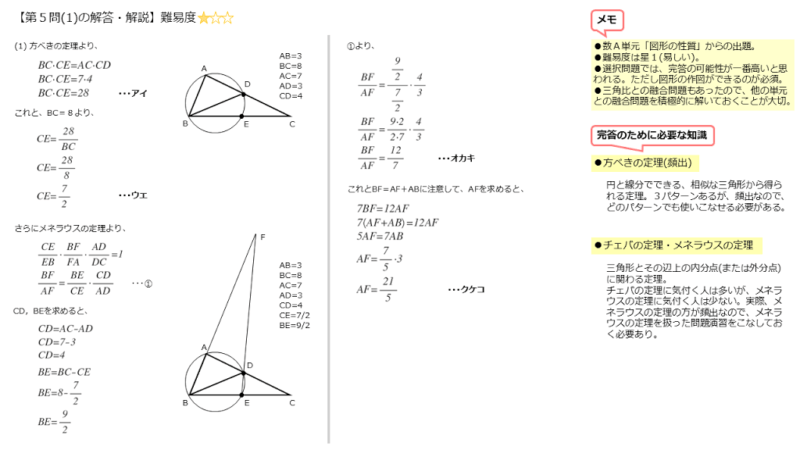
方べきの定理より
\begin{align*} \quad BC \cdot CE = AC \cdot CD \end{align*}ここで
\begin{align*} &\quad AC=7 \\[ 7pt ] &\quad CD=AC-AD=7-3=4 \end{align*}より
\begin{align*} \quad BC \cdot CE = 7 \cdot 4 \end{align*}よって
\begin{align*} \quad BC \cdot CE = 28 \end{align*}また、BCの長さが分かっているので、式を変形してCEの長さを求めます。
解答欄ウエの解答例
\begin{align*} &\vdots \\[ 7pt ] \quad BC \cdot CE &= 28 \end{align*}これと
\begin{align*} \quad BC=8 \end{align*}より
\begin{align*} \quad CE = \frac{28}{8} \end{align*}よって
\begin{align*} \quad CE = \frac{7}{2} \end{align*}解答欄アイ,ウエの記述例は以下の通りです。
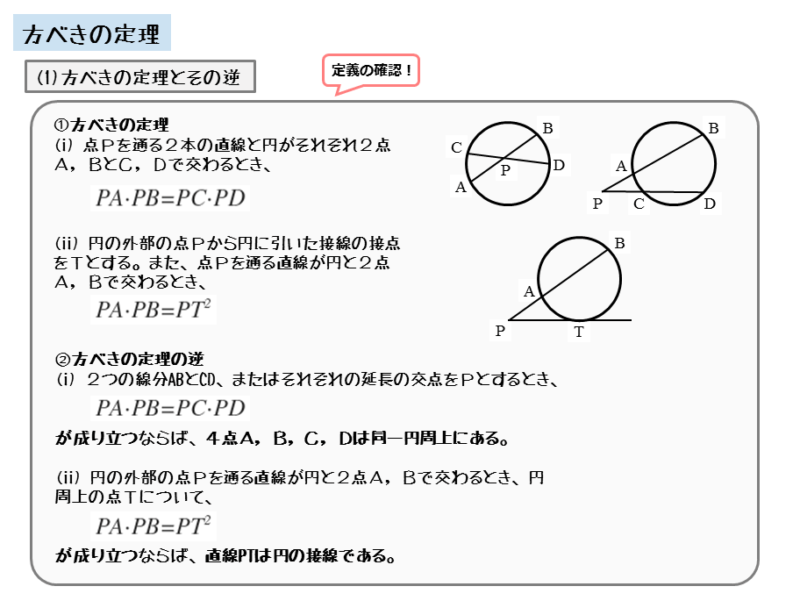
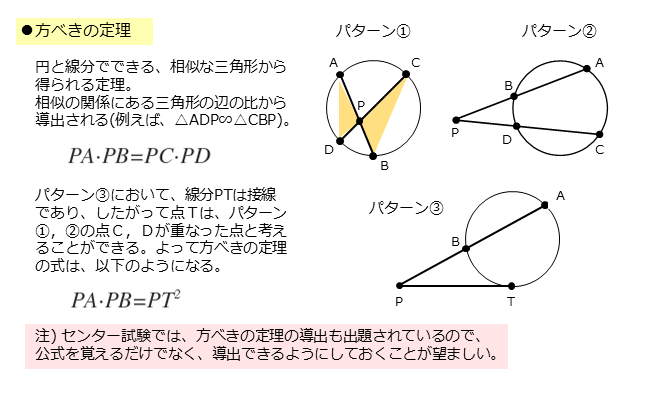
ところで、方べきの定理を利用できる図形には3パターンあるので、使い分けができるようにしておきましょう。
解答欄オカキ,クケコ
解答欄オカキ,クケコ
条件1
$\triangle {ABC}$ おいて、$AB=3 \ , \ BC=8 \ , \ AC=7$
条件2
辺 $AC$ 上に $AD=3$ となる点 $D$ をとる。
条件3
$\triangle {ABD}$ の外接円と直線 $BC$ の交点で $B$ と異なるものを $E$ とする。
条件4
$CE=7/2$
このとき
$BF/AF$ の値(解答欄オカキ)
$AF$ の値(解答欄クケコ)
条件4,5が増えたのは、アイ,ウエの問題を解いたからです。これらも場合によっては利用します。
解答欄オカキに関する問題は、2つの線分BF,AFの長さの比の値BF/AFを求める問題です。また、解答欄クケコに関する問題はAFの値を求める問題です。
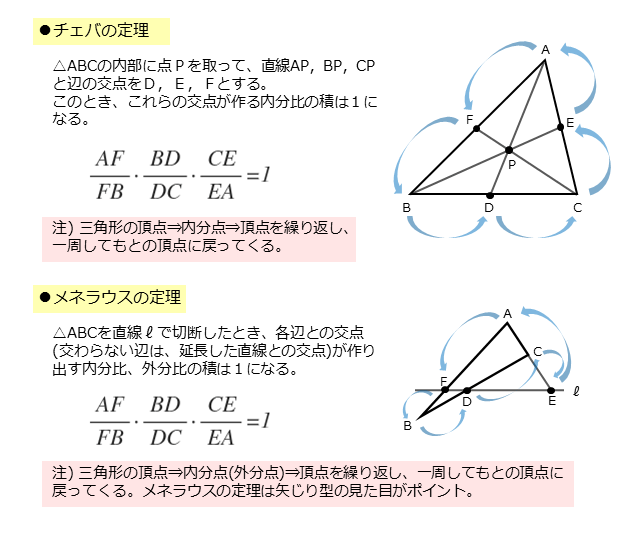
長さ比の値を利用したものとしては「メネラウスの定理」や「チェバの定理」があります。作図の様子から、メネラウスの定理を利用できそうです。
メネラウスの定理が利用できるとき、図形は「矢じり型」のようになっている。チェバの定理よりもメネラウスの定理の方が出題率が高いので、図形とセットで覚えておこう。
図を参考にして、メネラウスの定理を使って立式します。
解答欄オカキの解答例
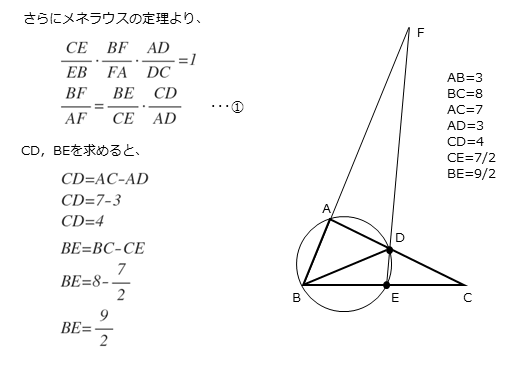
メネラウスの定理より
\begin{align*} \quad \frac{CE}{EB} \cdot \frac{BF}{FA} \cdot \frac{AD}{DC} = 1 \end{align*}これを整理すると
\begin{align*} \quad \frac{FB}{FA} = \frac{BE}{CE} \cdot \frac{CD}{AD} \end{align*}ここで
\begin{align*} \quad AD=3 \ , \ CD=4 \ , \ CE=\frac{7}{2} \end{align*}また
\begin{align*} \quad BE &=BC-CE \\[ 7pt ] &=8-\frac{7}{2} \\[ 7pt ] &=\frac{9}{2} \end{align*}より
\begin{align*} \quad \frac{FB}{FA} = \frac{\frac{9}{2}}{\frac{7}{2}} \cdot \frac{4}{3} \end{align*}整理すると
\begin{align*} \quad \frac{FB}{FA} = \frac{12}{7} \end{align*}立式したらBF/AFについて変形し、右辺に4つの線分の長さをそれぞれ代入して整理します。ただし、 線分 BEの長さを求めておく必要があります。
また、AFの値は、BF/AFとBF=AF+ABであることに注意して解きます。(1)は基本的レベルの問題なので、手早く解いてしまいましょう。
解答欄クケコの解答例
\begin{align*} &\vdots \\[ 7pt ] \quad \frac{FB}{FA} &= \frac{12}{7} \end{align*}これに
\begin{align*} \quad BF=AF+AB \end{align*}を代入すると
\begin{align*} \quad \frac{AF+AB}{FA} = \frac{12}{7} \end{align*}$AF$ について整理すると
\begin{align*} \quad 7\left(AF+AB \right) &=12AF \\[ 7pt ] 5AF &=7AB \\[ 7pt ] AF &=\frac{7}{5}AB \end{align*}$AB=3$ より
\begin{align*} \quad AF =\frac{21}{5} \end{align*}解答欄オカキ,クケコの記述例は以下の通りです。
なお、チェバの定理やメネラウスの定理では、その覚え方にコツがあります。
どちらの定理でも、スタートした頂点に必ず戻ってくるように、またアルファベットがつながるように式を作ることができます。先に矢印を書き込んで立式すると、間違いを減らせます。
第5問(1)の解答例とポイントをまとめると以下のようになります。
次は第5問(2)を解いてみましょう。