図形の性質｜２円の位置関係について
今回は、２円の位置関係について学習しましょう。
この単元に関する問題は、新課程以前ではよく出題されていました。それに対して新課程になると、あまり見かけなくなりました。あくまでも傾向なので、きちんと対応できる準備は必要です。
円だけを扱った問題であれば特に難しくありません。しかし、他の図形（三角形や四角形など）との融合問題になると、正答率が低く、差が付きやすくなります。
おそらく複数の図形が絡むので、より複雑になったことが原因かもしれません。できることなら、複数の図形を一緒に扱った入試レベルの問題をこなしておいた方が良いでしょう。
記事の画像が見辛いときはクリックすると拡大できます。
２円の位置関係と共通接線
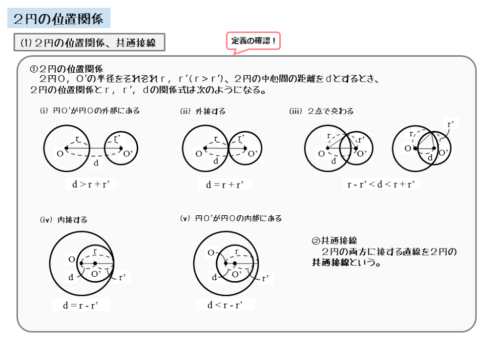
２つの円があるとき、それらの位置関係は５種類に分類されます。
２円の位置関係
- 円Ｏ’が円Ｏの外部にある。
- ２円Ｏ，Ｏ’が外接する。
- ２円Ｏ，Ｏ’が２点で交わる。
- ２円Ｏ，Ｏ’が内接する。
- 円Ｏ’が円Ｏの内部にある。
この５種類の位置関係に応じて、線分の長さを求めたり、線分の長さの大小関係を考えたりする問題が出題されます。
また、２つの円を扱う問題では共通接線もよく扱われます。
共通接線とは、複数の図形に対して同時に接している直線のことです。１本の直線がそれぞれの図形と接点だけを共有しています。
複数の図形に対して、共通接線を何本引けるかなどの問題がよく出題されます。
２円の中心間距離と２円の半径との関係
２円の位置関係によって、２円の中心間距離と２円の半径との関係が変わるので注意しましょう。作図しながら考えるとよく分かります。
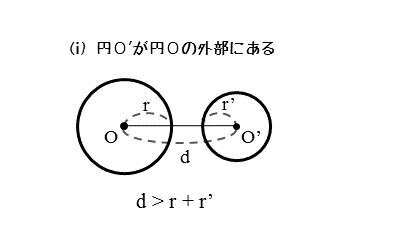
円Ｏ’が円Ｏの外部にあるとき
２円Ｏ，Ｏ’の半径をそれぞれｒ，ｒ’、２円の中心間距離をｄとします。
円Ｏ’が円Ｏの外部にあるとき、図から分かるように、中心間距離ｄは、２円の半径の和(ｒ＋ｒ’)よりも大きくなります。このときの関係を不等式で表すと以下のようになります。
円Ｏ’が円Ｏの外部にあるとき
円$O’$ が円 $O$ の外部にあるとき、$2$ 円の中心間距離と半径の関係は
\begin{align*} \quad d \gt r+r’ \end{align*}ただし
\begin{align*} \quad d &\cdots \text{$2$ 円の中心間距離} \\[ 5pt ] r &\cdots \text{円 $O$ の半径} \\[ 5pt ] r’ &\cdots \text{円 $O’$ の半径} \end{align*}
２円Ｏ，Ｏ’が外接するとき
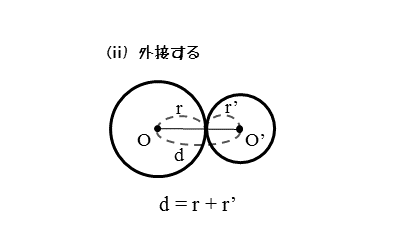
２円Ｏ，Ｏ’が外接するとき、図から分かるように、中心間距離ｄは、２円の半径の和(ｒ＋ｒ’)に等しくなります。このときの関係を等式で表すと以下のようになります。
２円Ｏ，Ｏ’が外接するとき
$2$ 円$O \ , \ O’$ が外接するとき、$2$ 円の中心間距離と半径の関係は
\begin{align*} \quad d = r+r’ \end{align*}ただし
\begin{align*} \quad d &\cdots \text{$2$ 円の中心間距離} \\[ 5pt ] r &\cdots \text{円 $O$ の半径} \\[ 5pt ] r’ &\cdots \text{円 $O’$ の半径} \end{align*}
２円Ｏ，Ｏ’が2点で交わるとき
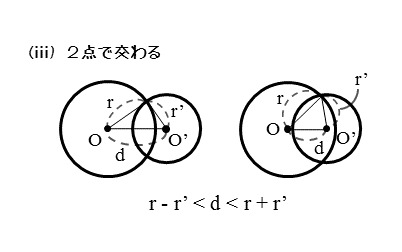
２円Ｏ，Ｏ’が２点で交わるとき、図から分かるように、中心間距離ｄは、２円の半径の和(ｒ＋ｒ’)よりも小さくなり、２円の半径の差|ｒ－ｒ’|よりも大きくなります。
このときの関係を不等式で表すと以下のようになります。
２円Ｏ，Ｏ’が２点で交わるとき
$2$ 円$O \ , \ O’$ が $2$ 点で交わるとき、$2$ 円の中心間距離と半径の関係は
\begin{align*} \quad \left|r-r’ \right| \lt d \lt r+r’ \end{align*}ただし
\begin{align*} \quad d &\cdots \text{$2$ 円の中心間距離} \\[ 5pt ] r &\cdots \text{円 $O$ の半径} \\[ 5pt ] r’ &\cdots \text{円 $O’$ の半径} \end{align*}
一般に、差は絶対値をつけて表されます。図では、ｒ＜ｒ’であるとして、差に絶対値をつけていません。以下の図でも同様です。
２円の中心間距離と半径の関係を表す不等式は、三角形の成立条件から導かれます。図のように、２円の中心と交点によって三角形において、三角形の成立条件を考えます。三角形の３辺の長さはｄ，ｒ，ｒ’です。
ちなみに、三角形の成立条件は以下のようになります。
三角形の成立条件
三角形が存在するとき、次の条件を満たす。
- ２辺の長さの和は、他の１辺の長さより大きい。
- ２辺の長さの差は、他の１辺の長さより小さい。
３辺の長さがｄ，ｒ，ｒ’である三角形において、この条件を考えます。
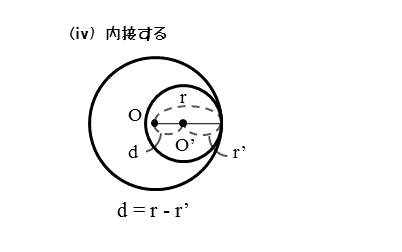
２円Ｏ，Ｏ’が内接するとき
２円Ｏ，Ｏ’が内接するとき、図から分かるように、中心間距離ｄは、２円の半径の差|ｒ－ｒ’|に等しくなります。このときの関係を不等式で表すと以下のようになります。
２円Ｏ，Ｏ’が内接するとき
$2$ 円$O \ , \ O’$ が内接するとき、$2$ 円の中心間距離と半径の関係は
\begin{align*} \quad d= \left| r-r’ \right| \end{align*}ただし
\begin{align*} \quad d &\cdots \text{$2$ 円の中心間距離} \\[ 5pt ] r &\cdots \text{円 $O$ の半径} \\[ 5pt ] r’ &\cdots \text{円 $O’$ の半径} \end{align*}
円Ｏ’が円Ｏの内部にあるとき
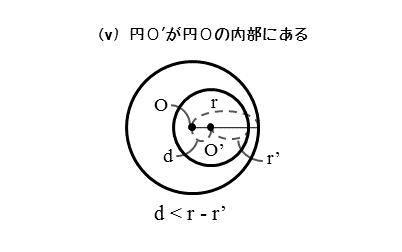
円Ｏ’が円Ｏの内部にあるとき、図から分かるように、中心間距離ｄは、２円の半径の差|ｒ－ｒ’|よりも小さくなります。この関係を不等式で表すことができます。
円Ｏ’が円Ｏの内部にあるとき
円 $O’$ が円 $O$ の内部にあるとき、$2$ 円の中心間距離と半径の関係は
\begin{align*} \quad d \lt \left| r-r’ \right| \end{align*}ただし
\begin{align*} \quad d &\cdots \text{$2$ 円の中心間距離} \\[ 5pt ] r &\cdots \text{円 $O$ の半径} \\[ 5pt ] r’ &\cdots \text{円 $O’$ の半径} \end{align*}
円Ｏ’が円Ｏの内部にあるとき、不等式をよく間違えるので注意しましょう。
次は、２円に接する共通接線の本数を考えてみましょう。
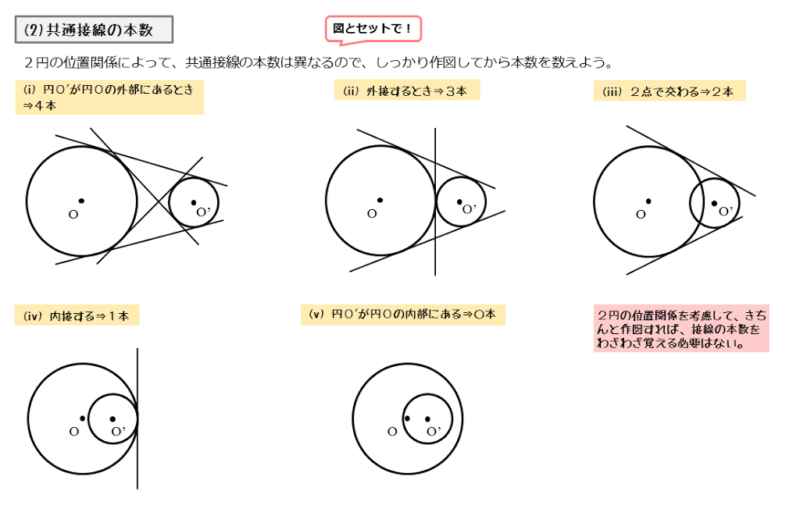
２円の位置関係と共通接線の本数の関係
２つの円が共通接線をもつとき、共通接線はそれぞれの円と１点（接点）で交わります。どちらの円にも同時に接しているのが共通接線です。
この共通接線の本数は、２円の位置関係によって異なります。実際に作図して調べてみましょう。
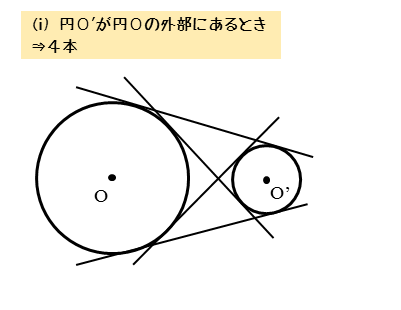
円Ｏ’がＯの外部にあるとき
円Ｏ’がＯの外部にあるとき、図のように共通接線を引けます。このとき、４本の共通接線を引くことができます。
また、円Ｏ’が円Ｏの外部にあるので、２円は共有点をもちません。
ここで注意したいのは、円と共通接線の共有点（接点）は、それぞれの円上にあって、同じ点ではないことです。よく勘違いする人がいるので注意しましょう。
また、共通接線と円との共有点（接点）と、２つの円の共有点（交点）を混同しないようにしましょう。何と何の共有点なのかを把握しましょう。図示すれば間違うことはないので、必ず図を見て確認しましょう。
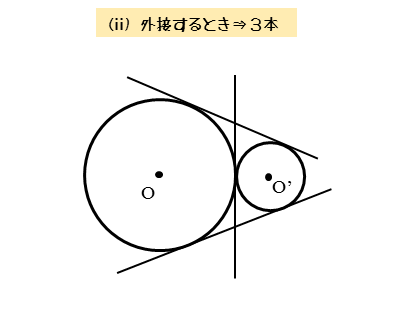
２円Ｏ，Ｏ’が外接するとき
２円Ｏ，Ｏ’が外接するとき、図のように共通接線を引けます。このとき、３本の共通接線を引くことができます。
また、２円Ｏ，Ｏ’が外接するので、２円は共有点を１個（接点）だけもちます。
なお、３本の共通接線のうち１本は、２円の共有点を接点とする直線です。この場合、２円の共有点は、接点に一致します。
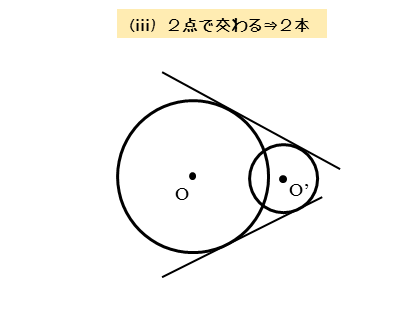
２円Ｏ，Ｏ’が２点で交わる
２円Ｏ，Ｏ’が２点で交わるとき、図のように共通接線を引けます。このとき、２本の共通接線を引くことができます。
２円Ｏ，Ｏ’が２点で交わるので、２円は共有点を２個もちます。また、円と共通接線の共有点（接点）は、それぞれの円上にあります。
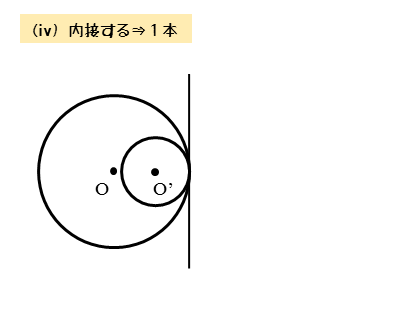
２円Ｏ，Ｏ’が内接するとき
２円Ｏ，Ｏ’が内接するとき、図のように共通接線を引けます。このとき、１本の共通接線を引くことができます。
２円Ｏ，Ｏ’が内接するので、２円は共有点を１個もちます。この共有点は、円と共通接線の共有点（接点）に一致します。
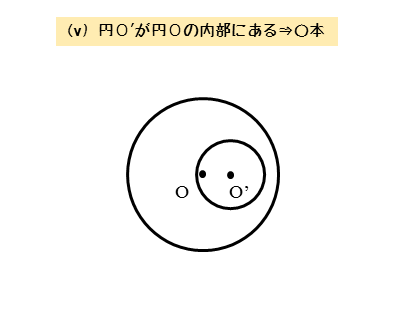
円Ｏ’が円Ｏの内部にある
円Ｏ’が円Ｏの内部にあるとき、２円の位置関係から共通接線を引くことができないので、共通接線は０本です。
また、円Ｏ’が円Ｏの内部にあるので、２円は共有点をもちません。
２円の位置関係と共通接線の本数をまとめると以下のようになります。
次は、2つの円と共通接線を扱った図形において、接点間の距離を考えてみましょう。
接点間の距離
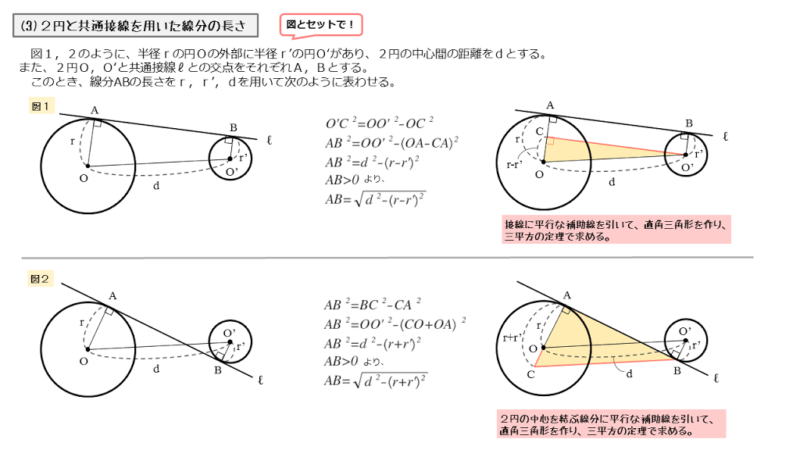
２円と共通接線を扱った図形では、共通接線の本数のほかに、接点間の距離（図では線分ＡＢ）を扱った問題が出題されます。
接点間の距離を扱った問題は、共通接線の引き方によって２パターンに分類されます。
図が与えられている場合が多いですが、自分で少し手を加える必要があります。作図の手順をきちんと覚えましょう。
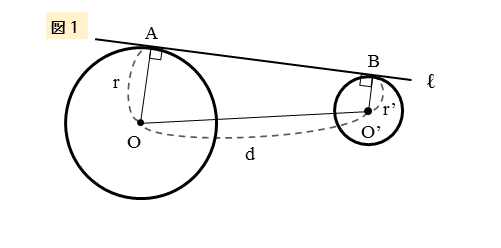
接点が同じ側にあるときの接点間の距離
１つ目のパターンは、図１のように、共通接線との接点がともに同じ側（図では上側）にある図形です。
２円Ｏ，Ｏ’と共通接線ℓとの接点をそれぞれＡ，Ｂとします。
また、２円Ｏ，Ｏ’の半径をｒ，ｒ’、中心間距離をｄとします。
このとき、接点間の距離である線分ＡＢの長さを、ｒ，ｒ’，ｄを用いて表してみましょう。
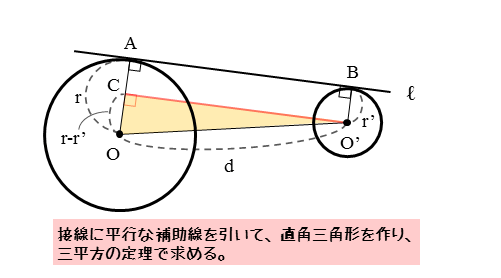
中心Ｏ’を通り、接線ℓに平行な直線を引き、この直線と線分ＯＡの交点をＣとします。
このとき、ＯＡ⊥ℓ，ＯＢ⊥ℓであるので、ＯＡ⊥Ｏ’Ｃ，ＯＢ⊥Ｏ’Ｃです。これより、△ＯＯ’Ｃは直角三角形です。
△ＯＯ’Ｃの一辺である辺Ｏ’Ｃは線分ＡＢに等しいので、線分ＡＢの長さを求めるには、辺Ｏ’Ｃの長さを求めれば良いことが分かります。
△ＯＯ’Ｃが直角三角形なので、三平方の定理を利用して辺Ｏ’Ｃの長さを求めます。
接点間距離
$\triangle OO’C$ において、三平方の定理より
\begin{align*} \quad {OO’}^2 = {OC}^2 + {O’C}^2 \end{align*}ここで
\begin{align*} \quad OO’ &= d \\[ 7pt ] OC &= r-r’ \\[ 7pt ] O’C &= AB \end{align*}より
\begin{align*} \quad d^2 = {\left(r-r’ \right)}^2 + {AB}^2 \end{align*}よって
\begin{align*} \quad {AB}^2 = d^2 – {\left(r-r’ \right)}^2 \end{align*}$AB \gt 0$ より
\begin{align*} \quad AB = \sqrt{ d^2 – {\left(r-r’ \right)}^2 } \end{align*}ＡＢに平行な直線を引いて、ＡＢをＯ’Ｃに平行移動。
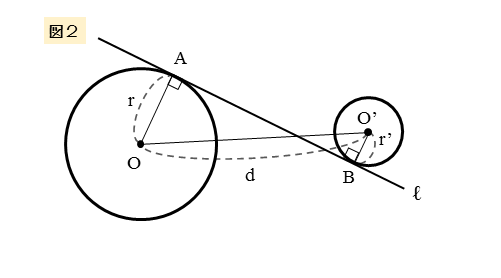
接点が異なる側にあるときの接点間の距離
２つ目のパターンは、図２のように、共通接線との接点が異なる側（図ではＡが上側、Ｂが下側）にある図形です。
２円Ｏ，Ｏ’と共通接線ℓとの接点をそれぞれＡ，Ｂとします。
また、２円Ｏ，Ｏ’の半径をｒ，ｒ’、中心間距離をｄとします。
このとき、接点間の距離である線分ＡＢの長さを、ｒ，ｒ’，ｄを用いて表してみましょう。
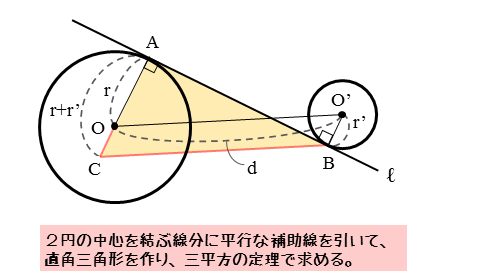
接点Ｂを通り、直線ＯＯ’に平行な直線を引き、この直線と直線ＯＡの交点をＣとします。
このとき、ＯＡ⊥ℓであるので、△ＡＢＣは直角三角形です。
平行線の引き方がパターン１とは異なるので注意しましょう。
ちなみに、中心Ｏ’を通り、直線ℓに平行な直線を引いても直角三角形（△ＯＯ’Ｃ）をつくれます。こちらの方が１つ目のパターンと手順が同じで覚えやすいかもしれません。
接点間の距離は辺ＡＢの長さに等しいですが、線分ＡＢは△ＡＢＣの一辺です。直角三角形である△ＡＢＣにおいて、三平方の定理を利用して辺ＡＢの長さを求めます。
接点間距離
$\triangle ABC$ において、三平方の定理より
\begin{align*} \quad {BC}^2 = {AB}^2 + {AC}^2 \end{align*}ここで
\begin{align*} \quad BC &= d \\[ 7pt ] AC &= r+r’ \end{align*}より
\begin{align*} \quad d^2 = {AB}^2 + \left(r+r’ \right)^2 \end{align*}よって
\begin{align*} \quad {AB}^2 = d^2 – \left(r+r’ \right)^2 \end{align*}$AB \gt 0$ より
\begin{align*} \quad AB = \sqrt{ d^{2} – \left(r+r’ \right)^{2} } \end{align*}ＯＯ’に平行な直線を引いて、ＯＯ’をＢＣに平行移動。
どちらのパターンであっても作図の仕方を知っておけば、式を覚える必要はありません。計算も三平方の定理を利用した計算なので、２辺の長さを求めてから計算すれば、それほど難しくありません。
接点間の距離のポイントをまとめると以下のようになります。
次は、２円の位置関係を扱った問題を実際に解いてみましょう。