図形と方程式｜円外の点から円に引いた接線について

08/07/2022数学２

今回は、円外の点から円に引いた接線について学習しましょう。

接線に関する問題は、単純な図形としてだけでなく、方程式などと絡めて出題されます。入試でも頻出で、共通テストレベルから大学別の個別試験レベルまで様々です。

分野をまたぐ融合問題のせいで意外と難易度が高いので、何度も演習を重ねておきましょう。

円の接線の方程式

円の接線の方程式は、以下のように表されます。

円の接線の方程式

円 $x^{2}+y^{2}=r^{2}$ 上の点 $P(x_{1} \ , \ y_{1})$ における接線の方程式は

$\begin{align*} \quad x_{1} \ x+y_{1} \ y=r^{2} \end{align*}$

ただし

$\begin{align*} \quad {x_{1}}^{2}+{y_{1}}^{2}=r^{2} \end{align*}$

円の方程式と接点の座標が与えられていれば、円の接線の方程式を求めることができます。公式があるので、対応する数を代入するだけで済みます。

ところで、この公式はどのようにして導出されるのでしょうか。公式を覚えるのは良いことですが、自分で導出できるようになっておきましょう。

互いに垂直な２直線の傾きの積を利用して導出すると、以下のようになります。

円の接線の方程式を導出する 1⃣

円の方程式と接点の座標をそれぞれ

$\begin{align*} &\quad x^{2}+y^{2}=r^{2} \\[ 7pt ] &\quad P \ (x_{1} \ , \ y_{1}) \end{align*}$

とする。このとき、接点は円上の点であるので

$\begin{align*} \quad {x_{1}}^{2}+{y_{1}}^{2}=r^{2} \quad \cdots \text{①} \end{align*}$

$[ \ 1 \ ] \ x_{1}=0 \ , \ y_{1} \neq 0$ のとき

接線は $y$ 軸に垂直であり、その方程式は

$\begin{align*} \quad y=y_{1} \end{align*}$

$[ \ 2 \ ] \ x_{1} \neq 0 \ , \ y_{1}=0$ のとき

接線は $x$ 軸に垂直であり、その方程式は

$\begin{align*} \quad x=x_{1} \end{align*}$

$[ \ 3 \ ] \ x_{1} \neq 0 \ , \ y_{1} \neq 0$ のとき

接線は点 $P$ を通るので、傾きを $m$ とすると

$\begin{align*} \quad y-y_{1} = m \left(x-x_{1} \right) \quad \cdots \text{②} \end{align*}$

ここで、中心と接点を通る直線と接線とは垂直なので

$\begin{align*} \quad m \cdot \frac{y_{1}}{x_{1}}=-1 \end{align*}$

より

$\begin{align*} \quad m =-\frac{x_{1}}{y_{1}} \end{align*}$

これと②より

$\begin{align*} \quad y-y_{1} = -\frac{x_{1}}{y_{1}} \left(x-x_{1} \right) \end{align*}$

整理すると

$\begin{align*} \quad x_{1}x+y_{1}y={x_{1}}^{2}+{y_{1}}^{2} \end{align*}$

①より

$\begin{align*} \quad x_{1}x+y_{1}y=r^{2} \end{align*}$

これは $[ \ 1 \ ] \ , \ [ \ 2 \ ]$ のときも満たす。

したがって、円 $x^{2}+y^{2}=r^{2}$ 上の点 $P(x_{1} \ , \ y_{1})$ における接線の方程式は

$\begin{align*} \quad x_{1}x+y_{1}y=r^{2} \end{align*}$

接線がｘ，ｙ軸に垂直である場合と、そうでない場合を区別した方が記述しやすいので、場合分けしています。

また、点と直線の距離を利用して導出すると、以下のようになります。

円の接線の方程式を導出する 2⃣

円の方程式と接点の座標をそれぞれ

$\begin{align*} &\quad x^{2}+y^{2}=r^{2} \\[ 7pt ] &\quad P \ (x_{1} \ , \ y_{1}) \end{align*}$

とする。このとき、接点は円上の点であるので

$\begin{align*} \quad {x_{1}}^{2}+{y_{1}}^{2}=r^{2} \quad \cdots \text{①} \end{align*}$

$[ \ 1 \ ] \ x_{1}=0 \ , \ y_{1} \neq 0$ のとき

接線は $y$ 軸に垂直であり、その方程式は

$\begin{align*} \quad y=y_{1} \end{align*}$

$[ \ 2 \ ] \ x_{1} \neq 0 \ , \ y_{1}=0$ のとき

接線は $x$ 軸に垂直であり、その方程式は

$\begin{align*} \quad x=x_{1} \end{align*}$

$[ \ 3 \ ] \ x_{\scriptsize{1}} \neq 0 \ , \ y_{\scriptsize{1}} \neq 0$ のとき

接線は点 $P$ を通るので、傾きを $m$ とすると

$\begin{align*} \quad y-y_{1} = m \left(x-x_{1} \right) \quad \cdots \text{②} \end{align*}$

すなわち

$\begin{align*} \quad mx-y-mx_{1}+y_{1} = 0 \end{align*}$

と表せる。円の中心と接線との距離は半径に等しいので

$\begin{align*} \quad \frac{\left| m \cdot 0-0-mx_{1}+y_{1} \right|}{\sqrt{m^{2}+(-1)^{2}}}=r \end{align*}$

よって

$\begin{align*} \quad \frac{ \left| -mx_{1}+y_{1} \right| }{ \sqrt{m^{2}+1} }=r \end{align*}$

両辺を $2$ 乗すると

$\begin{align*} \quad \frac{\left(-mx_{1}+y_{1} \right)^{2} }{ m^{2}+1 }=r^{2} \end{align*}$

両辺に $m^{\scriptsize{2}}+1$ を掛けて

$\begin{align*} \quad \left(-mx_{1}+y_{1} \right)^{2}=r^{2} \left(m^{2}+1 \right) \end{align*}$

①より

$\begin{align*} \quad \left(-mx_{1}+y_{1} \right)^{2}=\left({x_{1}}^{2}+{y_{1}}^{2} \right)\left(m^{2}+1 \right) \end{align*}$

整理すると

$\begin{align*} &\quad {x_{1}}^{2}+2m x_{1} y_{1}+m^{2} {y_{1}}^{2}=0 \\[ 7pt ] &\quad \left(x_{1}+my_{1} \right)^{2}=0 \end{align*}$

よって

$\begin{align*} \quad x_{\scriptsize{1}}+my_{\scriptsize{1}}=0 \end{align*}$

より

$\begin{align*} \quad m=-\frac{ x_{1} }{ y_{1} } \end{align*}$

これと②より

$\begin{align*} \quad y-y_{1} = -\frac{x_{1}}{y_{1}} \left(x-x_{1} \right) \end{align*}$

整理すると

$\begin{align*} \quad x_{1}x+y_{1}y={x_{1}}^{2}+{y_{1}}^{2} \end{align*}$

①より

$\begin{align*} \quad x_{1}x+y_{1}y=r^{2} \end{align*}$

これは $[ \ 1 \ ] \ , \ [ \ 2 \ ]$ のときも満たす。

したがって、円 $x^{2}+y^{2}=r^{2}$ 上の点 $P(x_{1} \ , \ y_{1})$ における接線の方程式は

$\begin{align*} \quad x_{1}x+y_{1}y=r^{2} \end{align*}$

傾きを用いた直線の方程式では、ｙ軸に垂直な直線を表すことができても、ｘ軸に垂直な直線を表すことはできません。ですから、場合分けして接線の方程式を考えた方が分かりやすいでしょう。

ここでは３パターンに場合分けしましたが、２パターンで済みます。

基本的な導出法を２つ挙げました。なお、ベクトルを学習すれば、法線ベクトルを利用した導出法もあります。

円外の点から円に引いた接線の方程式

円の接線を求めるとき、円の方程式と接点の座標が与えられていれば良いですが、そうでないときもあります。

円外の点から円に引いた接線を考えます。最初に与えられる情報は、円の方程式と円外の点の座標です。残念ながら、接点の座標は与えられません。

接点の座標さえ分かれば、円の方程式が与えられているので、接線の公式を利用できます。ですから、何とかして接点の座標を求める必要があります。

接点の座標を求めるためには、接点のｘ，ｙ座標についての方程式が必要になります。その方程式は、円と接線の方程式からそれぞれ得られます。

接線の方程式や接点の座標を求める流れは、以下のようになります。

円外の点から引いた円の接線の求め方

接点の座標を定義する
接点は円上の点 ⇒ 接点の座標を円の方程式に代入
公式から円の接線を求める
接線は円外の点を通る ⇒ 円外の点の座標を接線の方程式に代入
２，４から、２つの方程式を連立して解く ⇒ 接点の座標
接点の座標を接線の方程式に代入

接線を扱った問題で、接点の座標が与えられていなければ、まず接点の座標を定義するのが定石です。これは、円の接線に限りません。他のグラフに接する接線でも同様です。

円外の点から円に引いた接線を求めてみよう

次の例題を解いてみましょう。

例題

点 $(3 \ , \ 1)$ を通り、円 $x^{2}+y^{2}=2$ に接する直線の方程式と、そのときの接点の座標を求めよ。

点(３，１)は、円外の点であって、接点ではありません。座標を円の方程式に代入すると分かります。

円外の点を接点と間違わないこと

$\begin{align*} \quad x^{2}+y^{2}=2 \end{align*}$

この左辺に $x=3 \ , \ y=1$ を代入すると

$\begin{align*} \quad (\text{左辺})=3^{2}+1^{2}=10 \end{align*}$

より

$\begin{align*} \quad (\text{左辺}) \neq (\text{右辺}) \end{align*}$

等式が成り立たないので、点 $(3 \ , \ 1)$ は円上の点ではない。

与えられた円の方程式に座標を代入すると、等式が成り立ちません。等式が成り立たないので、与えられた座標は、方程式の解ではないということです。

このことから、与えられた点(３，１)は、円上の点ではないことが分かります。よく間違うので注意しましょう。

例題の解答・解説

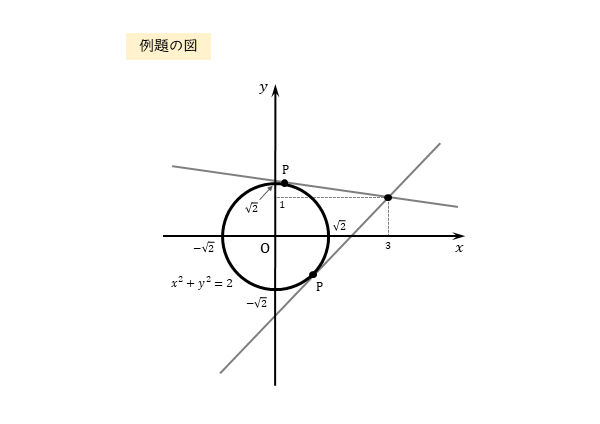
図示すると以下のようになります。

作図すると分かりますが、円外の点から円に引いた接線は、２本あります。このことを踏まえて解きましょう。

接点の座標を定義します。接点は円上の点であるので、座標を円の方程式に代入すると、等式が成り立ちます。

例題の解答例 1⃣

接点を

$\begin{align*} \quad P(x_{1} \ , \ y_{1}) \end{align*}$

とすると

$\begin{align*} \quad {x_{1}}^{2}+{y_{1}}^{2}=2 \quad \cdots \text{①} \end{align*}$

これで１つ目の方程式①を導くことができました。

次に、公式を利用して、接線の方程式を求めます。接線は点(３，１)を通るので、この点の座標を接線の方程式に代入すると、等式が成り立ちます。

例題の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad {x_{1}}^{2}+{y_{1}}^{2}=2 \quad \cdots \text{①} \end{align*}$

また、点 $P$ における円の接線の方程式は

$\begin{align*} \quad x_{1}x+y_{1}y=2 \end{align*}$

この直線が点 $(3 \ , \ 1)$ を通るので

$\begin{align*} \quad 3x_{1}+y_{1}=2 \quad \cdots \text{②} \end{align*}$

これで２つ目の方程式②を導くことができました。

２つの方程式を連立して解きます。連立方程式の解が接点のｘ，ｙ座標です。代入法を利用してｙ₁を消去し、ｘ₁についての方程式を導きます。

例題の解答例 3⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad {x_{1}}^{2}+{y_{1}}^{2}=2 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad 3x_{1}+y_{1}=2 \quad \cdots \text{②} \end{align*}$

①，②から $y_{1}$ を消去して

$\begin{align*} \quad {x_{1}}^{2}+\left(2-3x_{1} \right)^{2}=2 \end{align*}$

整理すると

$\begin{align*} \quad 5{x_{1}}^{2}-6x_{1}+1=0 \end{align*}$

これを解くと

$\begin{align*} \quad \left(5x_{1}-1 \right)\left(x_{1}-1 \right)=0 \end{align*}$

よって

$\begin{align*} \quad x_{1}=\frac{1}{5} \ , \ 1 \end{align*}$

接点のｘ座標が分かったので、ｙ座標を求めます。ただし、ｘ座標は２つあるので、場合分けします。

例題の解答例 4⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad {x_{1}}^{2}+{y_{1}}^{2}=2 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad 3x_{1}+y_{1}=2 \quad \cdots \text{②} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad x_{\scriptsize{1}}=\frac{1}{5} \ , \ 1 \end{align*}$

これと②から

$\begin{align*} &x_{1}=\frac{1}{5} \ \text{のとき} \quad y_{1}=\frac{7}{5} \\[ 7pt ] &x_{1}=1 \ \text{のとき} \quad y_{1}=-1 \end{align*}$

それぞれの接点について、接線の方程式を求めます。

例題の解答例 5⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x_{1}x+y_{1}y=2 \\[ 7pt ] &\quad \vdots \\[ 7pt ] &x_{1}=\frac{1}{5} \ \text{のとき} \quad y_{1}=\frac{7}{5} \\[ 7pt ] &x_{1}=1 \ \text{のとき} \quad y_{1}=-1 \end{align*}$

したがって、求める接線の方程式と接点の座標は

$\begin{align*} &\quad x+7y=10 \ , \ \left(\frac{1}{5} \ , \ \frac{7}{5} \right) \\[ 7pt ] &\quad x-y=2 \ , \ (1 \ , \ -1) \end{align*}$

連立方程式を解くのが少し難しいかもしれません。加減法では上手くいかないので、代入法を利用しましょう。

接点がなければ、自分で定義することからスタート。

例題の別解１

上述の解答例がこの単元での模範解答です。これ以外にも、これまでの学習内容を利用して解くこともできます。接点と重解の関係を利用した解法です。

接点は２つの図形の共有点です。共有点の座標は、２つの図形の方程式を連立したときの解です。２つの図形の共有点は接点の１つだけなので、連立方程式から得られる解は１組だけです。

たとえば、円と直線の方程式を連立すると、ｘ座標についての２次方程式を導くことができます。この２次方程式は、共有点が１つだけなので、解を１つしかもちません。解が１つとは、重解のことです。

２次方程式が重解をもつとき、判別式の値は０となります。この性質を利用して、接点の座標を求めます。

接線が点(３，１)を通るので、傾きを定義して接線の方程式をつくります。

例題の別解例１ 1⃣

点 $(3 \ , \ 1)$ を通る接線は $x$ 軸に垂直でないので、求める接線の方程式は傾きを $m$ とすると

$\begin{align*} \quad y-1 = m\left(x-3 \right) \end{align*}$

すなわち

$\begin{align*} \quad y = mx-\left(3m-1 \right) \quad \cdots \text{③} \end{align*}$

接線がｘ軸に垂直でないことを断っておきましょう。

円と接線の方程式から、ｘについての２次方程式を導きます。

例題の別解例１ 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y = mx-\left(3m-1 \right) \quad \cdots \text{③} \end{align*}$

③を円の方程式に代入して整理すると

$\begin{align*} &\quad x^{2}+\left\{ mx-\left(3m-1 \right) \right\}^{2}=2 \\[ 7pt ] &\quad x^{2}+m^{2}x^{2}-2m\left(3m-1 \right)x+\left(3m-1 \right)^{2}=2 \\[ 7pt ] &\quad \left(m^{2}+1 \right)x^{2}-2m\left(3m-1 \right)x+\left\{ \left(3m-1 \right)^{2}-2 \right\}=0 \quad \cdots \text{④} \end{align*}$

ここでは解きませんが、この方程式の解は、共有点である接点のｘ座標になります。

２次方程式④から判別式Ｄを導きます。係数や定数項に気を付けましょう。

例題の別解例１ 3⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left(m^{2}+1 \right)x^{2}-2m\left(3m-1 \right)x+\left\{ \left(3m-1 \right)^{2}-2 \right\}=0 \quad \cdots \text{④} \end{align*}$

$m^{2}+1 \neq 0$ であるので、④の判別式を $D$ とすると

$\begin{align*} \quad \frac{D}{4} &= \left\{ m\left(3m-1 \right) \right\}^{2}-\left(m^{2}+1 \right) \left\{ \left(3m-1 \right)^{2}-2 \right\} \\[ 7pt ] &= m^{2} \left(3m-1 \right)^{2}-\left(m^{2}+1 \right)\left(3m-1 \right)^{2} +2\left(m^{2}+1 \right) \\[ 7pt ] &= \left\{ m^{2}-\left(m^{2}+1 \right) \right\} \left(3m-1 \right)^{2}+2\left(m^{2}+1 \right) \\[ 7pt ] &= -\left(3m-1 \right)^{2}+2\left(m^{2}+1 \right) \\[ 7pt ] &= -9m^{2}+6m-1+2m^{2}+2 \\[ 7pt ] &= -7m^{2}+6m+1 \\[ 7pt ] &= -\left(7m+1 \right)\left(m-1 \right) \end{align*}$

判別式を導くとき、むやみに展開せず、共通因数でくくるなどして、工夫しながら整理しましょう。

２次方程式④が重解をもつのは、判別式Ｄの値が０のときです。

例題の別解例１ 4⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad =-\left(7m+1 \right)\left(m-1 \right) \end{align*}$

円と直線③が接するための条件は $D=0$ であるので

$\begin{align*} \quad -\left(7m+1 \right)\left(m-1 \right)=0 \end{align*}$

よって

$\begin{align*} \quad m=-\frac{1}{7} \ , \ 1 \end{align*}$

ｍは接線の傾きです。ｍの値が２つあるので、接線は２つあります。

ｍの値それぞれについて、接線の方程式と、接点のｘ座標である重解を求めます。重解を求めるとき、公式を利用しましょう。

また、重解と接線の方程式を利用して、接点のｙ座標を求めます。計算量が多いので注意しましょう。

例題の別解例１ 5⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y = mx-\left(3m-1 \right) \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad \left(m^{2}+1 \right)x^{2}-2m\left(3m-1 \right)x+\left\{ \left(3m-1 \right)^{2}-2 \right\}=0 \quad \cdots \text{④} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad m=-\frac{1}{7} \ , \ 1 \end{align*}$

ここで、④の重解は

$\begin{align*} \quad x &= -\frac{-2m\left(3m-1 \right)}{2\left(m^{2}+1 \right)} \\[ 7pt ] &= \frac{m\left(3m-1 \right)}{m^{2}+1} \quad \cdots \text{⑤} \end{align*}$

$[ \ 1 \ ] \quad m=-\frac{1}{7}$ のとき

接線の方程式は③より

$\begin{align*} \quad y=-\frac{1}{7}x+\frac{10}{7} \quad \cdots \text{⑥} \end{align*}$

重解は⑤より

$\begin{align*} \quad x=\frac{-\frac{1}{7}\left\{3 \cdot \left(-\frac{1}{7} \right)-1\right\} }{\left(-\frac{1}{7} \right)^{2}+1}=\frac{1}{5} \end{align*}$

これと⑥より

$\begin{align*} \quad y=\frac{7}{5} \end{align*}$

$[ \ 2 \ ] \quad m=1$ のとき

接線の方程式は③より

$\begin{align*} \quad y=x-2 \quad \cdots \text{⑦} \end{align*}$

重解は⑤より

$\begin{align*} \quad x=\frac{1 \cdot \left(3 \cdot 1-1 \right)}{1^{2}+1}=1 \end{align*}$

これと⑦より

$\begin{align*} \quad y=-1 \end{align*}$

$[ \ 1 \ ] \ , \ [ \ 2 \ ]$ より、求める接線の方程式と接点の座標は

$\begin{align*} &\quad y=-\frac{1}{7}x+\frac{10}{7} \ , \ \left(\frac{1}{5} \ , \ \frac{7}{5} \right) \\[ 7pt ] &\quad y=x-2 \ , \ (1 \ , \ -1) \end{align*}$

この解法では、接点と重解の関係を利用しています。この解法の利点は、円と直線の関係以外にも利用できることです。接点に関わる問題は、円と直線だけではないので、そんなときに接点と重解の関係は重宝します。

また、２次方程式の重解を求めるとき、方程式を解くのではなく、公式を利用しましょう。

２次方程式の重解

$2$ 次方程式

$\begin{align*} \quad ax^{2}+bx+c=0 \end{align*}$

において、 $D=0$ のときの重解は

$\begin{align*} \quad x=-\frac{b}{2a} \end{align*}$

例題の別解２

もう１つ別解があります。点と直線の距離を利用した解法です。

円と直線の位置関係についてはすでに学習しています。円と直線が接するとき、円の中心と直線との距離は、円の半径に等しくなります。このことを利用します。

図形と方程式｜円と直線の位置関係について

接線が点(３，１)を通るので、傾きを定義して接線の方程式をつくります。

例題の別解例２ 1⃣

点 $(3 \ , \ 1)$ を通る接線は $x$ 軸に垂直でないので、求める接線の方程式は、傾きを $m$ とすると

$\begin{align*} \quad y-1 = m\left(x-3 \right) \end{align*}$

すなわち

$\begin{align*} \quad y = mx-\left(3m-1 \right) \end{align*}$

これを整理すると

$\begin{align*} \quad mx-y-3m+1=0 \quad \cdots \text{⑧} \end{align*}$

ここまでは別解１と同じ流れです。ただし、点と直線の距離を利用するので、接線の方程式を一般形に変形しておきます。

円の中心と接線との距離を求めます。円の半径に等しくなります。

例題の別解例２ 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad mx-y-3m+1=0 \quad \cdots \text{⑧} \end{align*}$

円の中心 $(0 \ , \ 0)$ と接線の距離が円の半径 $\sqrt{2}$ に等しいので

$\begin{align*} \quad \frac{\left| m \cdot 0-0-3m+1 \right|}{ \sqrt{m^{2}+(-1)^{2}} } = \sqrt{2} \end{align*}$ よって

$\begin{align*} \quad \frac{\left| -3m+1 \right|}{\sqrt{m^{2}+1}} = \sqrt{2} \end{align*}$

ｍについての方程式を導くことができました。これを変形して、解を求めます。

例題の別解例２ 3⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{\left| -3m+1 \right|}{\sqrt{m^{2}+1}} = \sqrt{2} \end{align*}$

両辺に $\sqrt{m^{\scriptsize{2}}+1}$ を掛けて

$\begin{align*} \quad \left| -3m+1 \right| = \sqrt{2\left(m^{2}+1 \right)} \end{align*}$

両辺を $2$ 乗して整理すると

$\begin{align*} &\quad \left(-3m+1 \right)^{2} = 2\left(m^{2}+1 \right) \\[ 7pt ] &\quad 9m^{2}-6m+1 = 2m^{2}+2 \\[ 7pt ] &\quad 7m^{2}-6m-1 = 0 \\[ 7pt ] &\quad \left(7m+1 \right)\left(m-1 \right)=0 \end{align*}$

よって

$\begin{align*} \quad m=-\frac{1}{7} \ , \ 1 \end{align*}$

点と直線の距離を利用した解法でも、ｍについての２次方程式を解くことになります。

それぞれのｍの値について、⑧式から接線の方程式を求めます。次は、接点Ｐのｘ座標と言いたいところですが、別解１と異なり、円と直線の方程式から導いた２次方程式がありません。

そこで、接線と半径ＯＰが垂直になることを利用します。

半径ＯＰの方程式は、原点と点Ｐを通る直線なので簡単に得られます。接線と直線ＯＰの方程式を連立させて、接点Ｐの座標を求めます。

例題の別解例２ 4⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad mx-y-3m+1=0 \quad \cdots \text{⑧} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad m=-\frac{1}{7} \ , \ 1 \end{align*}$

$[ \ 1 \ ] \quad m=-\frac{1}{7}$ のとき

接線の方程式は⑧より

$\begin{align*} \quad x+7y-10=0 \quad \cdots \text{⑨} \end{align*}$

ここで、直線 $OP$ は

$\begin{align*} \quad 7 \cdot \left(x-0 \right)-1 \cdot \left(y-0 \right)=0 \end{align*}$

より

$\begin{align*} \quad y=7x \end{align*}$

これと⑨を連立させて解くと

$\begin{align*} \quad x=\frac{1}{5} \ , \ y=\frac{7}{5} \end{align*}$

よって、接点の座標は

$\begin{align*} \quad \left(\frac{1}{5} \ , \ \frac{7}{5} \right) \end{align*}$

$[ \ 2 \ ] \quad m=1$ のとき

接線の方程式は⑧より

$\begin{align*} \quad x-y-2=0 \quad \cdots \text{⑩} \end{align*}$

ここで、直線 $OP$ は

$\begin{align*} \quad -1 \cdot \left(x-0 \right)-1 \cdot \left(y-0 \right)=0 \end{align*}$

より

$\begin{align*} \quad y=-x \end{align*}$

これと⑩を連立させて解くと

$\begin{align*} \quad x=1 \ , \ y=-1 \end{align*}$

よって、接点の座標は

$\begin{align*} \quad (1 \ , \ -1) \end{align*}$

$[ \ 1 \ ] \ , \ [ \ 2 \ ]$ より、求める接線の方程式と接点の座標は

$\begin{align*} &\quad x+7y-10=0 \ , \ \left(\frac{1}{5} \ , \ \frac{7}{5} \right) \\[ 7pt ] &\quad x-y-2=0 \ , \ (1 \ , \ -1) \end{align*}$

接点の座標を求めるとき、円と接線の方程式を連立させても構いません。ただし、接線と直線ＯＰのときよりも計算量が増えるので注意しましょう。

また、直線ＯＰの方程式を求めるとき、接線の方程式が一般形であることを利用しています。

垂直な直線の方程式を一般形で表すと、以下のようになります。ただし、１点の座標が必要です。

垂直な直線の方程式

点 $(x_{1} \ , \ y_{1})$ を通り、直線

$\begin{align*} \quad ax+by+c=0 \end{align*}$

に垂直な直線の方程式は

$\begin{align*} \quad b \left(x-x_{1} \right)-a \left(y-y_{1} \right)=0 \end{align*}$

これは $a=0$ または $b=0$ の場合も成り立つ。

この公式を利用すれば、直線ＯＰの方程式を簡単に求めることができます。

図形と方程式｜平行または垂直な直線の方程式について

解法が複数あるときは問題に応じて使い分けよう

例題を解くには、３つの解法があります。３つの解法の利点をまとめると、以下のようになります。

問題に応じて解法を使い分けよう

【解法１】円の接線の公式を利用：接点の座標と接線の方程式を求める問題に適する。計算量は少ない。
【解法２】接点 ⇔ 重解を利用：円と直線の関係以外にも利用できる。計算量はやや多い。
【解法３】中心と接線の距離＝半径を利用：接点の座標を求める必要がない問題に適する。計算量はやや多い。

それぞれの解法に良さがあります。問題に応じて使い分けられるようになりましょう。

次は、円外の点から円に引いた接線を扱った問題を実際に解いてみましょう。

数学２円,図形と方程式,接線

Posted by kiri

知らなきゃ損するセキュリティ対策｜ウイルスの基礎

$数学を学習するときに実践したいこと$

数学を学習するときに実践したいことについて