図形と方程式｜折れ線の長さの最小について
今回は、折れ線の長さの最小について学習しましょう。折れ線のままで考えると、長さの最小値を求めることが難しくなります。
図を見ながら考えると、視覚的に理解できるでしょう。
折れ線の長さ
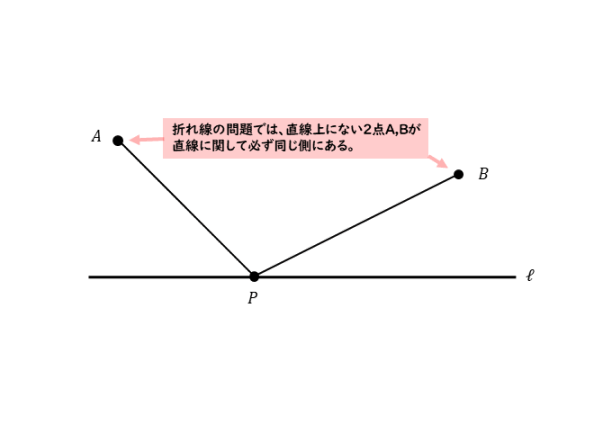
直線上にない２点Ａ，Ｂがあります。この２点は直線に対して同じ側にあります。
たとえば、点Ａが直線の上側にあれば、点Ｂも同じように直線の上側にあります。この２点Ａ，Ｂと直線上の点Ｐを結びます。
２点Ａ，Ｂは直線上にない点です。ですから、線分ＡＰと線分ＰＢはつながってはいますが、まっすぐではなく、折れ曲がっています。
このような線分ＡＰと線分ＰＢの長さの和、すなわち折れ線の長さを考えます。
折れ線の長さ＝ＡＰ＋ＰＢ
このような折れ線について、その長さが最小になるとき、点Ｐは直線上のどこにあれば良いでしょうか。
線対称な点をつくる
折れ線のままで点Ｐの位置を考えるのはとても難しいです。折れ線になるのは、２点Ａ，Ｂが直線に関して同じ側にあるからです。
これを解決するために、線対称な図形の性質を利用します。線対称な図形の性質を利用すると、２点のうち一方を、直線に関して他方とは反対側にとることができます。
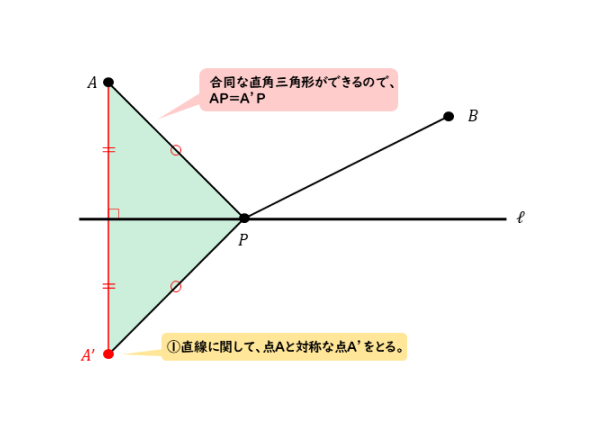
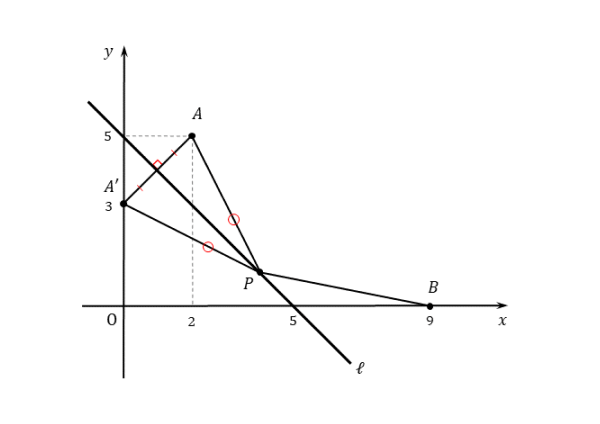
直線ℓを対称の軸として、点Ａと線対称な点を作ります。点Ａの代わりに点Ｂでも構いません。図では、点Ａと直線ℓに関して対称な点Ａ’を作っています。
２点Ａ，Ａ’は対応する点なので、直線ℓまでの距離は等しくなります。また、線分ＡＡ’は直線ℓに垂直です。
ですから、対称の軸である直線ℓは、線分ＡＡ’の垂直二等分線となります。
線分ＡＡ’，ＡＰ，Ａ’Ｐによって三角形ができており、これが直線ℓによって二等分されています。
二等分されてできた２つの三角形は、直角三角形であり、合同な図形です。ですから、２つの線分ＡＰ，Ａ’Ｐの長さは等しくなります。
２つの線分ＡＰ，Ａ’Ｐの関係から、ＡＰ＋ＰＢはＡ’Ｐ＋ＰＢに等しいことが分かります。これは、点Ｐが直線ℓ上のどこにあっても成り立つ関係です。
点Ａと直線ℓに関して線対称な点Ａ’をとって、ＡＰ＝Ａ’Ｐを利用する。
線分で結ぶ
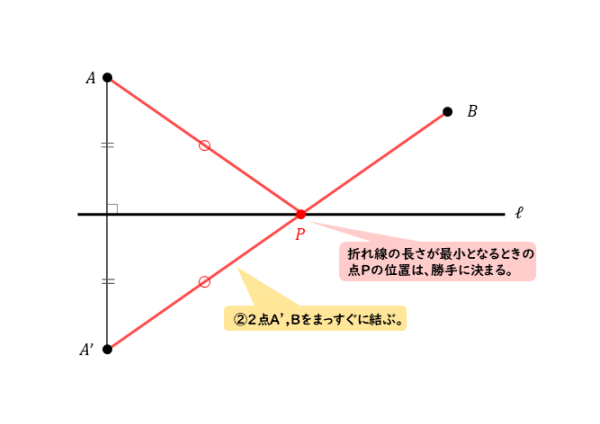
線対称な点を作れたらあとは簡単です。２点Ａ’，Ｂ間の最短経路は、２点Ａ’、Ｂを結んだ線分Ａ’Ｂです。このとき、折れ線の長さが最小となります。
作図では点Ａ’と点Ｂをまっすぐな線で結ぶだけです。
自分で点Ｐの位置を決める必要はありません。線分Ａ’Ｂを引けば、点Ｐの位置が勝手に決まるからです。点Ｐの位置を自分で頑張って探す必要はありません。
直線ℓと線分Ａ’Ｂとの交点がＰ
折れ線の長さの最小を求めてみよう
折れ線の長さの最小となる点Ｐの座標を求めてみましょう。
例題
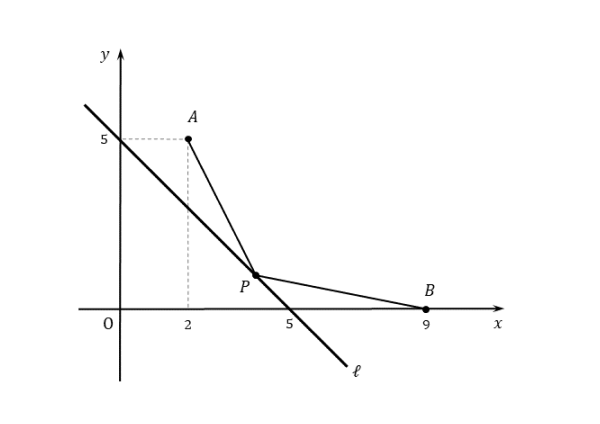
$A(2 \ , \ 5) \ , \ B(9 \ , \ 0)$ とするとき、直線 $x+y=5$ 上に点 $P$ をとり、$AP+PB$ を最小にする点 $P$ の座標を求めよ。
例題の解答・解説
作図は以下の通りです。与えられた情報を整理するために、作図することを心掛けましょう。
２点Ａ，Ｂが直線に関して同じ側にあることを確認しましょう。
ＡＰ＋ＢＰは折れ線の長さです。この折れ線の長さを最小にするときを考えます。
まず、直線ｘ＋ｙ＝５を対称の軸として、点Ａと線対称な点Ａ’を作り、その座標を求めます。
線対称な点の座標の求め方はすでに学習済みです。２直線の垂直条件や中点の座標を利用します。
例題の解答例 1⃣
与えられた直線
\begin{align*} \quad x+y=5 \quad \cdots \text{①} \end{align*}をℓとする。
また、直線ℓに関して $A$ と対称な点を
\begin{align*} \quad A'(a \ , \ b) \end{align*}とする。
ここで直線 $AA’$ は $x$ 軸に垂直ではないので
\begin{align*} \quad a \neq 2 \end{align*}$AA’ \perp$ ℓであるので
\begin{align*} \quad \frac{b-5}{a-2} \cdot \left(-1 \right)=-1 \end{align*}整理すると
\begin{align*} \quad a-b=-3 \quad \cdots \text{②} \end{align*}線分 $AA’$ の中点が直線ℓ上にあるので
\begin{align*} \quad \frac{a+2}{2}+\frac{b+5}{2}=5 \end{align*}整理すると
\begin{align*} \quad a+b=3 \quad \cdots \text{③} \end{align*}②，③を解くと
\begin{align*} \quad a=0 \ , \ b=3 \end{align*}よって、点 $A’$ の座標は
\begin{align*} \quad A’ \ (0 \ , \ 3 ) \end{align*}解答例では、直線ＡＡ’がｘ軸に垂直でないことを確認しています。
傾きの分母が０となる可能性があるからです。答案では直線ＡＡ’がｘ軸と垂直でないことに言及しておきましょう。
確認のやり方は、点Ａと点Ａ’のｘ座標が同じかどうかを確認するだけです。２点Ａ，Ａ’のｘ座標が同じであれば、傾きの分母は０となるからです。
点Ａ’を図示すると以下の通りです。作図が上手であれば、点Ａ’の座標を推測することができます。
直線ℓに関して点Ａと線対称な点Ａ’ができたので、点Ｐの位置を決めます。
点Ａ’から点Ｐを経由して点Ｂへたどる経路を考えると、この経路が最短となるのは、３点Ａ’，Ｐ，Ｂが同一直線上にあるときです。
つまり、点Ｐが線分Ａ’Ｂ上にあれば良いことが分かります。このとき、折れ線の長さが最小となります。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad A’ \ (0 \ , \ 3 ) \end{align*}このとき
\begin{align*} \quad AP+PB=A’P+PB \geqq A’B \end{align*}よって、$3$ 点 $A’ \ , \ P \ , \ B$ が同じ直線上にあるとき、$AP+PB$ は最小になる。
折れ線の長さは、線分Ａ’Ｂの長さよりも短くなることはないので注意しましょう。
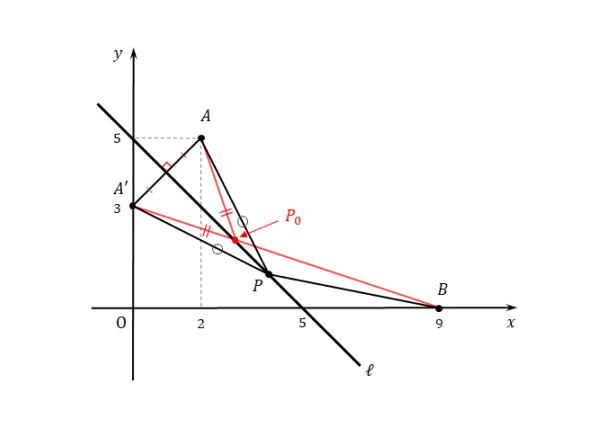
３点Ａ’，Ｐ，Ｂが同じ直線上にあるときの図は以下の通りです。
点Ｐが線分Ａ’Ｂ上にあるとき、点Ｐは線分Ａ’Ｂと直線ℓの交点となる位置にあります。
直線Ａ’Ｂの方程式を求め、交点の座標を求めます。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x+y=5 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad AP+PB=A’P+PB \geqq A’B \\[ 7pt ] &\quad \vdots \end{align*}直線 $A’B$ の方程式は、$2$ 点 $A'(0 \ , \ 3) \ , \ B(9 \ , \ 0)$ を通るので
\begin{align*} \quad \frac{x}{9}+\frac{y}{3}=1 \end{align*}よって
\begin{align*} \quad x+3y=9 \quad \cdots \text{④} \end{align*}直線 $A’B$ と直線ℓの交点を $P_{0}$ とすると、その座標は①，④を解いて
\begin{align*} \quad x=3 \ , \ y=2 \end{align*}よって
\begin{align*} \quad P_{0} \ (3 \ , \ 2) \end{align*}したがって、$AP+PB$ を最小にする点 $P$ の座標は $(3 \ , \ 2)$
直線Ａ’Ｂの方程式を求めるときは、ｘ切片とｙ切片を利用しましょう。
ｘ，ｙ切片を用いた直線の方程式
\begin{align*} \quad a \neq 0 \ , \ b \neq 0 \end{align*}のとき、$2$ 点
\begin{align*} \quad (a \ , \ 0) \ , \ (0 \ , \ b) \end{align*}を通る直線の方程式は
\begin{align*} \quad \frac{x}{a}+\frac{y}{b}=1 \end{align*}解法の手順をまとめてみましょう。
折れ線の長さの最小を求める手順
- 点Ａと直線ℓに関して線対称な点Ａ’をとり、点Ａ’と点Ｂを線分で結んだ図を描いておく。
- 点Ａ’の座標を求める。
- 直線Ａ’Ｂの方程式を求める。
- 直線Ａ’Ｂと直線ℓの交点（点Ｐ）の座標を求める。
結論が分かっているので、最初にきちんと作図しておきましょう。図を見ながら、点の座標や直線の方程式を求めていきます。求めた座標や方程式を図に追記しておくと良いでしょう。
次は、折れ線の長さの最小を扱った問題を実際に解いてみましょう。