図形と方程式｜直線に関して対称な点について
今回は、直線に関して対称な点について学習しましょう。直線に関して対称なので、線対称な図形の話です。
作図しながら考えると、理解しやすいでしょう。
直線に関して対称な点
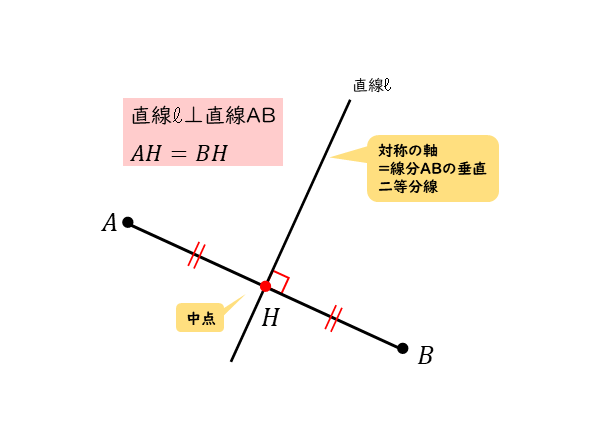
直線ℓに関して点Ａと対称な点Ｂを図示すると、以下のようになります。
点Ａと点Ｂは、直線ℓに関して対称なので、対応する点となります。線対称な図形では、対称の軸がありますが、これは直線ℓのことです。
対称の軸である直線ℓは、線分ＡＢに対して、垂直に、かつ二等分するように交わります。
このような直線ℓは、線分ＡＢの垂直二等分線となります。
直線ℓと直線ＡＢは垂直に交わるので、２直線の垂直条件を利用できます。
線分ＡＢと直線ℓとの交点をＨとすると、２つの線分ＡＨ，ＢＨの長さは等しく（ＡＨ＝ＢＨ）なります。ですから、点Ｈは線分ＡＢの中点です。
このことから、両端にある２点Ａ，Ｂの座標を用いれば、点Ｈの座標を表すことができます。
また、点Ｈは２直線ℓ，ＡＢの交点でもあるので、直線ℓ上にも直線ＡＢ上にもある点です。ですから、どちらの方程式に代入しても等式が成り立ちます。
このような性質を利用して問題を解くことになりますが、最低でも次の２点を覚えておきましょう。
直線ℓに関して２点Ａ，Ｂが対称であるとき
- 直線ＡＢは直線ℓに垂直 ⇒ ２直線の垂直条件が成り立つ。
- 線分ＡＢの中点は直線ℓ上にある ⇒ 直線ℓの方程式に座標を代入しても良い。
直線に関して対称な点を求めてみよう
直線に関して対称な点を求めてみましょう。
例題
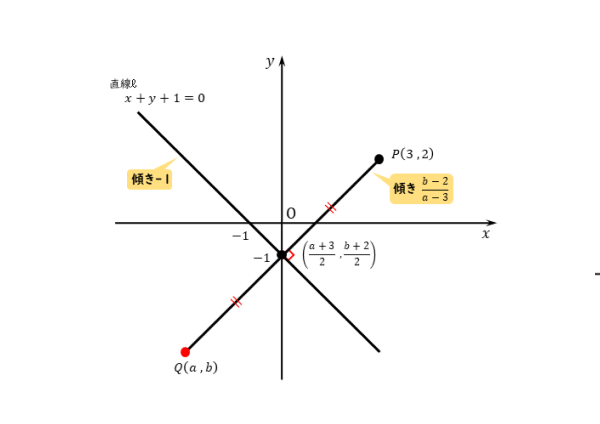
直線ℓ：$x+y+1=0$ に関して、点 $P \ (3 \ , \ 2)$ と対称な点 $Q$ の座標を求めよ。
例題の解答・解説
作図は以下の通りです。
線対称な図形がもつ性質を利用して解きましょう。
点Ｑの座標を求めるので、座標を定義しておきます。
ちなみに、点Ｑの座標は、２直線の垂直条件や中点の座標を利用するときに必要です。
点Ｑの座標を定義して、２直線の傾きをそれぞれ求めます。
例題の解答例 1⃣
点 $Q$ の座標を $(a \ , \ b)$ とする。
直線ℓの傾きは与式から
\begin{align*} \quad y=-x-1 \end{align*}であるので $-1$
ここで、直線 $PQ$ は $x$ 軸に垂直でないので
\begin{align*} \quad a \neq 3 \end{align*}よって、直線 $PQ$ の傾きは
\begin{align*} \quad \frac{b-2}{a-3} \end{align*}直線ＰＱの傾きは、ｙの増加量をｘの増加量で割った分数で表されます。このとき、分母に文字ａが含まれます。文字ａは点Ｑのｘ座標です。
もし、直線ＰＱがｘ軸に垂直であれば、２点Ｐ，Ｑのｘ座標は同じになり、分母の式の値が０になってしまいます。
これを防ぐために、分母が０とならない、言い換えると、２点Ｐ，Ｑのｘ座標が同じではないことを明示しておきます。
直線の傾きを使うときは、分母が０でない（直線がｘ軸に垂直でない）ことが条件
直線ＰＱは直線ℓに垂直なので、２直線の垂直条件を利用して、ａ，ｂについての方程式を導きます。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{b-2}{a-3} \end{align*}直線 $PQ$ が直線ℓに垂直であるので
\begin{align*} \quad (-1) \cdot \frac{b-2}{a-3}=-1 \end{align*}これを整理すると
\begin{align*} \quad a-b-1=0 \quad \cdots \text{①} \end{align*}２直線の傾きによる垂直条件を利用すると、①式を導くことができます。
２直線の垂直条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が垂直であるとき
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}が成り立つ。（垂直条件）
次に、線分ＰＱの中点の座標を求めます。線分ＰＱの両端にある２点Ｐ，Ｑの座標を利用します。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad a-b-1=0 \quad \cdots \text{①} \end{align*}また、線分 $PQ$ の中点の座標は
\begin{align*} \quad \left( \frac{a+3}{2} \ , \ \frac{b+2}{2} \right) \end{align*}であり、これが直線ℓ上にあるので、直線ℓの方程式に代入すると
\begin{align*} \quad \frac{a+3}{2}+\frac{b+2}{2}+1=0 \end{align*}これを整理すると
\begin{align*} \quad a+b+7=0 \quad \cdots \text{②} \end{align*}中点が直線ℓ上にあることを利用して、中点の座標を直線ℓの方程式に代入します。これでａ，ｂについての方程式を導くことができます。
ａ，ｂについての方程式を２つ得ることができたので、連立方程式を解きます。
例題の解答例 4⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad a-b-1=0 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a+b+7=0 \quad \cdots \text{②} \end{align*}①，②を連立させて解くと、①＋②より
\begin{align*} \quad a=-3 \end{align*}これと②より
\begin{align*} \quad b=-4 \end{align*}したがって、点 $Q$ の座標は
\begin{align*} \quad Q \ (-3 \ , \ -4) \end{align*}点Ｑのｘ座標ａとｙ座標ｂを求める必要があります。このとき、未知のもの（ａ，ｂ）が２つなので、方程式も２つ必要になります。
直線ℓに関して点Ｐに対称な点Ｑの座標を求める手順
- ２直線ℓ，ＰＱの垂直条件から、２直線の傾きを「傾きの積＝－１」に代入して方程式を導く。
- 直線ℓ上にある線分ＰＱの中点の座標を、直線ℓの方程式に代入して方程式を導く。
- 連立方程式を導くと、点Ｑの座標が分かる。
例題の別解例
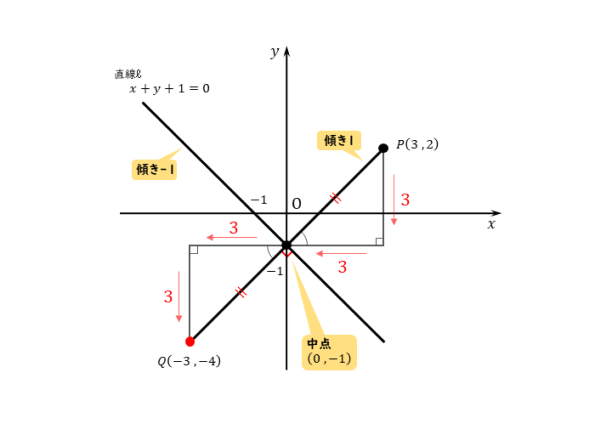
作図が丁寧だと、かなりの精度で求めたい座標が分かることがあります。
直線ℓの傾きは与式から－１です。このとき、垂直条件から直線ＰＱの傾きが１であることはすぐに分かります。
点Ｐを通り、直線ℓに垂直な直線を作図してみると、直線ℓとｙ軸との交点(０，－１)が線分ＰＱの中点になりそうだと予想できます。予想が正しいかを確認してみましょう。
点Ｐと点(０，－１)で傾きを求めてみると、直線ＰＱの傾きと一致します。ですから、点(０，－１)は直線ＰＱ上の点です。
また、直線ℓの方程式に点(０，－１)を代入すると等式が成り立つので、直線ℓ上の点でもあります。
このことから、点(０，－１)は２直線ℓ，ＰＱの交点であることが分かります。
直交する２直線ℓ，ＰＱの交点は、線対称な２点Ｐ，Ｑを結んだ線分の中点となることが分かっています。ですから、点(０，－１)は線分ＰＱの中点です。
線分ＰＱの中点の座標が分かれば、あとは簡単です。２点Ｐ，Ｑは対応する点です。上図のように合同な直角三角形を利用して、点Ｑの座標を図形的に求めることができます。点Ｑは、点Ｐから左に６、下に６だけ移動した点となります。
あまり褒められた解法ではありませんが、上手くはまれば簡単に解くことができます。マーク形式の試験であれば、過程を記述する必要がありません。間違った解法ではないので、このような解法でも良いでしょう。
次は、直線に関して対称な点を扱った問題を実際に解いてみましょう。