数学2
今回から「平面と方程式」という新しい章になります。ここでは、方程式から図形を描いたり、図形を方程式で表したりします。
図形を扱うので、積極的に作図するように心掛けましょう。作図できるかどうかは入試ではかなり重要です。
また、この章で学習したことは、後から学習する「ベクトル」とも深く関わるので、学習しているときに定着させておきましょう。
直線上の点
数直線上の点の表し方
直線に等間隔に目盛りを振って、点の位置を特定できるようにしたのが数直線です。
この数直線上に点があるとき、一次元なので、位置情報は1つで済みます。位置情報は座標のことです。
たとえば、数直線上の点Aがaという位置にあるとき、点Aの位置をA(a)と表します。
数直線上の2点間の距離
さて、このような数直線上にある2点間の距離を考えます。
原点Oと点Aとの間の距離であれば、線分OAの長さとなります。これはすでに学習した点Aの絶対値で求めることができます。
数直線上の2点間の距離 1⃣
\begin{align*}
&\text{原点 $O$ と点 $A(a)$ の距離は} \\[ 5pt ]
&\quad OA=|a|
\end{align*}
このように点の座標を用いれば、2点間の距離を求めることができます。
これは、原点からの距離ではなく、原点以外の2点間の距離であっても同じように求めることができます。たとえば、数直線上に点A(a)と点B(b)があるとします。この2点間の距離を考えてみましょう。
2点間の距離の求め方には、点A,Bの位置関係によって2通りあります。点Aが点Bの左側にあるときと右側にあるときです。
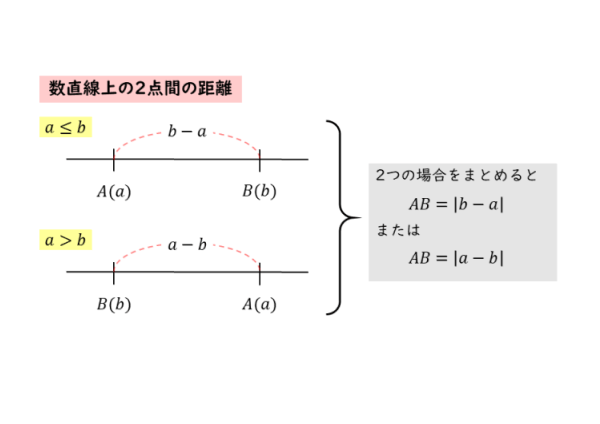 数直線上の2点間の距離
数直線上の2点間の距離 数直線では、正の向き(右向き)に進めば進むほど、座標が大きくなります。ですから、右側にある点の座標から左側にある点の座標を引き算すると、2点間の距離を求めることができます。
数直線上の2点間の距離 2⃣
\begin{align*}
&\text{$2$ 点 $A(a) \ , \ B(b)$ 間の距離は} \\[ 5pt ]
&\quad \text{$a \leqq b$ ならば} \quad AB=b-a \\[ 7pt ]
&\quad \text{$a \gt b$ ならば} \quad AB=a-b \\[ 7pt ]
&\text{これらをまとめると} \\[ 5pt ]
&\quad AB=|b-a| \\[ 7pt ]
&\text{または} \\[ 5pt ]
&\quad AB=|a-b|
\end{align*}
座標が文字で与えられる場合、座標の差の正負が分からないので、「a>bのとき」のように断りが必要になります。
いちいち断りを入れるのは面倒なので、上述のように絶対値の記号を利用します。これで座標の差の正負に関わらず、つねに絶対値(正の値)として扱うことができます。
座標の差を表す式は、どちらの座標から引いた式であっても問題ありません。無難なのは「右にある点の座標から左にある点の座標を引く」ことです。
数直線上の2点間の距離を求めてみよう
数直線上の2点間の距離を求めてみましょう。
例題1
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&(1) \quad A(-3) \ , \ B(2) \\[ 7pt ]
&(2) \quad A(-2) \ , \ B(-5)
\end{align*}
例題1(1)の解答・解説
例題1(1)
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&\quad A(-3) \ , \ B(2)
\end{align*}
数直線上の2点間の距離を求める問題です。点Bは点Aよりも右側にある点です。基本通り、点Bの座標から点Aの座標を引き算します。
例題1(1)の解答例
\begin{align*}
&\quad A(-3) \ , \ B(2) \\[ 7pt ]
&\text{$2$ 点 $A \ , \ B$ の距離は} \\[ 5pt ]
&\quad AB=|2-(-3)| \\[ 7pt ]
&\quad \quad =|5| \\[ 7pt ]
&\quad \quad =5
\end{align*}
別解は以下のようになります。点Aの座標から点Bの座標を引き算します。
例題1(1)の別解例
\begin{align*}
&\quad A(-3) \ , \ B(2) \\[ 7pt ]
&\text{$2$ 点 $A \ , \ B$ の距離は} \\[ 5pt ]
&\quad AB=|-3-2| \\[ 7pt ]
&\quad \quad =|-5| \\[ 7pt ]
&\quad \quad =-(-5) \\[ 7pt ]
&\quad \quad =5
\end{align*}
絶対値の記号を用いているので、最終的には正の値になります。ですから、どちらの点の座標から引き算しても問題ありません。
例題1(2)の解答・解説
例題1(2)
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&\quad A(-2) \ , \ B(-5)
\end{align*}
例題(1)と同じように、数直線上の2点間の距離を求める問題です。点Aは点Bよりも右側にある点です。基本通り、点Aの座標から点Bの座標を引き算します。
例題1(2)の解答例
\begin{align*}
&\quad A(-2) \ , \ B(-5) \\[ 7pt ]
&\text{$2$ 点 $A \ , \ B$ の距離は} \\[ 5pt ]
&\quad AB=|-2-(-5)| \\[ 7pt ]
&\quad \quad =|3| \\[ 7pt ]
&\quad \quad =3
\end{align*}
別解は以下のようになります。点Bの座標から点Aの座標を引き算します。
例題1(2)の別解例
\begin{align*}
&\quad A(-2) \ , \ B(-5) \\[ 7pt ]
&\text{$2$ 点 $A \ , \ B$ の距離は} \\[ 5pt ]
&\quad AB=|-5-(-2)| \\[ 7pt ]
&\quad \quad =|-3| \\[ 7pt ]
&\quad \quad =-(-3) \\[ 7pt ]
&\quad \quad =3
\end{align*}
解答例と別解例を比べると、座標の大きい方から小さい方を引き算した方が計算ミスしにくいことが分かります。基本通りの計算を心掛けましょう。
平面上の点
平面上の点の表し方
平面上にある点の場合だと、直線上にある場合に比べて少しだけ複雑になります。二次元になるので、位置情報が増えるからです。
互いに垂直な数直線を用いて、横方向と縦方向に分けて点の位置を表す必要があります。互いに垂直な数直線とは、グラフで用いられるx軸とy軸のことです。
横の位置情報と縦の位置情報をセットで扱うことで、点の位置を特定します。たとえば、A(1,2)などがそうです。
平面上の2点間の距離
このように平面上にある2点間の距離であっても、座標を用いれば求めることができます。
x軸方向の距離とy軸方向の距離については、数直線上の2点間の距離を利用してそれぞれ求めることができます。ただし、これでは平面上の2点間の距離を求めたことにはなりません。
ここからさらに図形的に2点間の距離を求めます。利用する図形的な知識は、三平方の定理です。
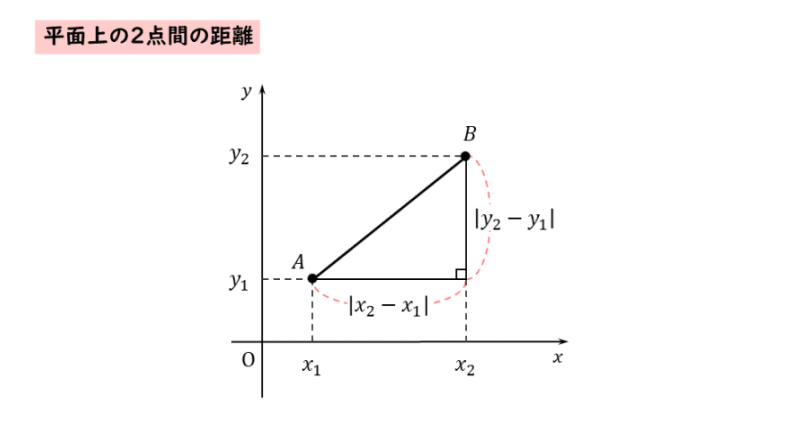 平面上の2点間の距離
平面上の2点間の距離 2点間の距離は、直角三角形の斜辺の長さに相当します。残りの2辺の長さはx軸方向の距離とy軸方向の距離に相当します。3辺の間には三平方の定理が成り立つので、2点間の距離を図形的に求めることができます。
平面上の2点間の距離 1⃣
\begin{align*}
&\text{座標平面上の $2$ 点 $A \ (x_{\scriptsize{1}} \ , \ y_{\scriptsize{1}}) \ , \ B \ (x_{\scriptsize{2}} \ , \ y_{\scriptsize{2}})$ 間の距離を求める。} \\[ 5pt ]
&\text{$x$ 軸方向の距離は} \\[ 5pt ]
&\quad |x_{\scriptsize{2}}-x_{\scriptsize{1}}| \\[ 7pt ]
&\text{$y$ 軸方向の距離は} \\[ 5pt ]
&\quad |y_{\scriptsize{2}}-y_{\scriptsize{1}}| \\[ 7pt ]
&\text{これと三平方の定理より} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}=|x_{\scriptsize{2}}-x_{\scriptsize{1}}|^{\scriptsize{2}}+|y_{\scriptsize{2}}-y_{\scriptsize{1}}|^{\scriptsize{2}} \\[ 7pt ]
&\text{すなわち} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}=\left(x_{\scriptsize{2}}-x_{\scriptsize{1}} \right)^{\scriptsize{2}}+\left(y_{\scriptsize{2}}-y_{\scriptsize{1}} \right)^{\scriptsize{2}} \\[ 7pt ]
&\text{$AB \gt 0$ より} \\[ 5pt ]
&\quad AB=\sqrt{\left(x_{\scriptsize{2}}-x_{\scriptsize{1}} \right)^{\scriptsize{2}}+\left(y_{\scriptsize{2}}-y_{\scriptsize{1}} \right)^{\scriptsize{2}}}
\end{align*}
特に、原点との距離は以下の通りです。
平面上の2点間の距離 2⃣
\begin{align*}
&\text{座標平面上の $2$ 点 $O \ (0,0) \ , \ B \ (x_{\scriptsize{1}} \ , \ y_{\scriptsize{1}})$ 間の距離を求める。} \\[ 5pt ]
&\text{$x$ 軸方向の距離は} \\[ 5pt ]
&\quad |x_{\scriptsize{1}}| \\[ 7pt ]
&\text{$y$ 軸方向の距離は} \\[ 5pt ]
&\quad |y_{\scriptsize{1}}| \\[ 7pt ]
&\text{これと三平方の定理より} \\[ 5pt ]
&\quad OA^{\scriptsize{2}}=|x_{\scriptsize{1}}|^{\scriptsize{2}}+|y_{\scriptsize{1}}|^{\scriptsize{2}} \\[ 7pt ]
&\text{すなわち} \\[ 5pt ]
&\quad OA^{\scriptsize{2}}={x_{\scriptsize{1}}}^{\scriptsize{2}}+{y_{\scriptsize{1}}}^{\scriptsize{2}} \\[ 7pt ]
&\text{$OA \gt 0$ より} \\[ 5pt ]
&\quad OA=\sqrt{{x_{\scriptsize{1}}}^{\scriptsize{2}}+{y_{\scriptsize{1}}}^{\scriptsize{2}}}
\end{align*}
式を覚えることは容易いですが、どうしてそうなるのかを理解しておくと応用が利くようになります。
平面上の2点間の距離を求めてみよう
平面上の2点間の距離を求めてみましょう。
例題2
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&(1) \quad A(-2 \ , \ 4) \ , \ B(7 \ , \ -3) \\[ 7pt ]
&(2) \quad O(0 \ , \ 0) \ , \ A(-6 \ , \ 8)
\end{align*}
例題2(1)の解答・解説
例題2(1)
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&\quad A(-2 \ , \ 4) \ , \ B(7 \ , \ -3)
\end{align*}
2点A,Bには、x座標とy座標が与えられています。例題2は、平面上の2点間の距離を求める問題です。公式の文字に対応する値を代入して計算しましょう。
例題2(1)の解答例
\begin{align*}
&\quad A(-2 \ , \ 4) \ , \ B(7 \ , \ -3) \\[ 7pt ]
&\text{$2$ 点 $A \ , \ B$ の距離は} \\[ 5pt ]
&\quad AB=\sqrt{\left\{7-(-2) \right\}^{\scriptsize{2}}+\left(-3-4 \right)^{\scriptsize{2}}} \\[ 7pt ]
&\quad \quad =\sqrt{81+49} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad AB=\sqrt{130}
\end{align*}
計算ミス、特に符号のミスに注意すれば易しい計算です。
例題(2)の解答・解説
例題2(2)
\begin{align*}
&\text{次の $2$ 点間の距離を求めよ。} \\[ 5pt ]
&\quad O(0 \ , \ 0) \ , \ A(-6 \ , \ 8)
\end{align*}
例題(1)と同じように、公式に値を代入して計算しましょう。
例題2(2)の解答例
\begin{align*}
&\quad O(0 \ , \ 0) \ , \ A(-6 \ , \ 8) \\[ 7pt ]
&\text{$2$ 点 $O \ , \ A$ の距離は} \\[ 5pt ]
&\quad OA=\sqrt{\left(-6 \right)^{\scriptsize{2}}+8^{\scriptsize{2}}} \\[ 7pt ]
&\quad \quad =\sqrt{100} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad OA=10
\end{align*}
2点のうち一方が原点であれば、残りの点の座標だけで2点間の距離を求めることができます。とても簡単な計算になります。
次は、平面上の2点間の距離を扱った問題を実際に解いてみましょう。














