図形と方程式|2つの円の位置関係について

今回は、2つの円の位置関係について学習しましょう。
2つの円の位置関係に関する問題は、入試でも頻出の問題です。共通テスト以前のセンター試験でもたびたび出題されています。
単体での出題であればそれほど難しくありませんが、入試レベルになると他の問題と併せて出題されるので難易度が上がります。
他の問題と併せて出題されると図形が複雑になりやすくなります。そのため作図が難しいのはもちろん、情報を整理するのが難しくなります。
日頃から演習の際に作図する習慣を身に付けておくことが大切です。
2つの円の位置関係
2つの円の半径と中心間距離の関係
2つの円の位置関係は、2つの円の半径と中心間距離の関係を調べることで分かります。
2つの円の半径と中心間距離の関係については、数学Aの分野ですでに学習しています。数学Aでは、2つの円の共有点の個数や共通接線について学習しました。
ちなみに、学習した内容は以下の通りです。
数学Aでは、2つの円の位置関係によって、「共有点が何個できるか」や「共通接線が何本ひけるか」を知るくらいのレベルでした。ですから、円の方程式を扱うことはありませんでした。
ここでは方程式との関係を学習するので、円の方程式を扱った問題が出題されます。
2つの円の半径と中心間距離の関係
ここでは、2つの円の半径と中心間距離の関係を調べるとき、円の方程式を用います。このとき、少し厄介なことがあります。円の方程式にaやkなどの変数が含まれることです。
このことを踏まえると、図中の半径と中心間距離の関係式(図:2円の位置関係、共通接線)を扱いやすい形にしておく必要があります。
ただし、ここでは2つの円が少なくとも共有点をもつ場合を考えるのが一般的です。図中の(ii),(iii),(iv)の場合です。
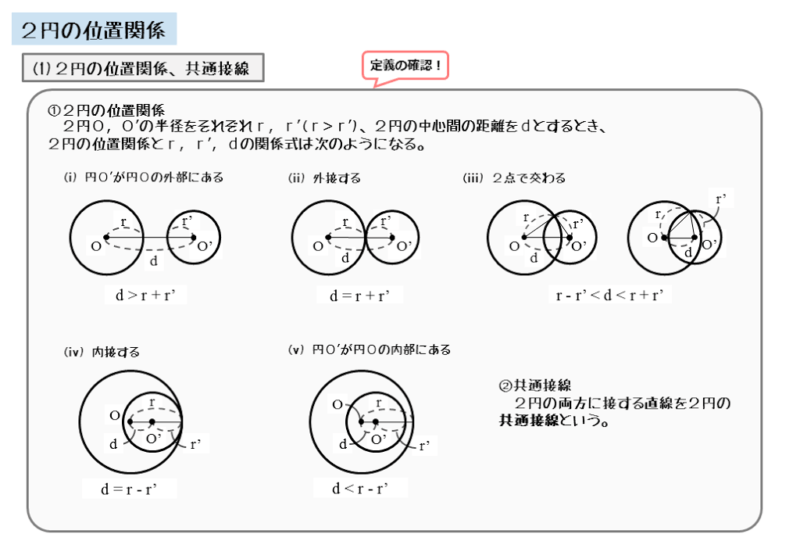
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とすると
$(1) \ 2$ つの円が外接する
\begin{align*} \quad d=r+r’ \end{align*}$(2) \ 2$ つの円が内接するか、一致する場合
\begin{align*} \quad d=\left| r-r’ \right| \end{align*}$(1) \ , \ (2)$ を合わせて、$2$ つの円が共有点をもつ場合
\begin{align*} \quad \left| r-r’ \right| \leqq d \leqq r+r’ \end{align*}2つの円が共有点をもつ場合の不等式には、絶対値記号が用いられています。扱いに注意しましょう。
以上を踏まえて例題を解いてみましょう。
2つの円の位置関係を調べてみよう
次の例題を解いてみましょう。
例題
$(1)$ 円 $C_{1} \ : \ x^{2}+y^{2}-6x-4y+9=0$ と点 $(-2 \ , \ 2)$ を中心とする円 $C_{2}$ が外接している。円 $C_{2}$ の方程式を求めよ。
$(2)$ $2$ つの円 $x^{2}+y^{2}=r^{2} \ (r \gt 0)$ … ①,$x^{2}+y^{2}-8x-4y+15=0$ … ②が共有点をもつような $r$ の値の範囲を求めよ。
どちらの問題も共有点をもつ場合です。
例題(1)の解答・解説
例題(1)
円 $C_{1} \ : \ x^{2}+y^{2}-6x-4y+9=0$ と点 $(-2 \ , \ 2)$ を中心とする円 $C_{2}$ が外接している。円 $C_{2}$ の方程式を求めよ。
例題(1)では、2つの円が外接するときの円の方程式を求めます。「一方の円の方程式」、「他方の円の中心」、「2つの円が外接する」という情報用いて、他方の円の方程式を求めます。
2つの円が外接するときの関係式を用いるために、2つの円の半径と中心間の距離を求める必要があります。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とする。
$2$ つの円が外接する条件は
\begin{align*} \quad d=r+r’ \end{align*}まず、円C1の方程式を変形して、中心と半径を求めます。
例題(1)の解答例 1⃣
円 $C_{1}$ の方程式を変形すると
\begin{align*} &\quad x^{2}+y^{2}-6x-4y+9=0 \\[ 7pt ] &\quad \left(x-3 \right)^{2}+\left(y-2 \right)^{2}=4 \end{align*}となるので、中心は点 $(3 \ , \ 2)$ で半径は $2$ である。
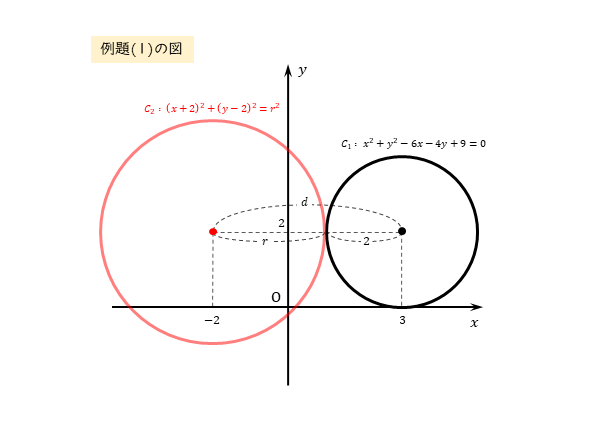
円C1の中心と半径が分かったので作図しておきます。作図することでよりイメージが鮮明になります。
円C2の半径が分かっていませんが、2つの円が外接するように作図しておきます。
作図が精確であれば、円C1の半径よりも大きくなりそうだと予想できます。場合によっては、図から求めることができることもあるので、できるだけ丁寧に作図しましょう。
円C1の方程式から中心が分かったので、2つの円の中心間距離を求めます。
例題(1)の解答例 2⃣
円 $C_{2}$ の中心は点 $(-2 \ , \ 2)$ であるので、$2$ つの円の中心間の距離 $d$ は
\begin{align*} \quad d &= \sqrt{ \left\{3- \left(-2 \right) \right\}^{2} + \left(2-2 \right)^{2} } \\[ 10pt ] &= \sqrt{ 5^{2} } \\[ 10pt ] &= 5 \end{align*}2つの円は外接するので、2つの円の中心間の距離は半径の和に等しくなります。この性質を利用して、円C2の半径を求めます。
例題(1)の解答例 3⃣
円 $C_{1} \ , \ C_{2}$ は外接するので、円 $C_{2}$ の半径を$r$ とすると
\begin{align*} \quad 2+r=5 \end{align*}よって
\begin{align*} \quad r=3 \end{align*}求める円 $C_{2}$ の方程式は
\begin{align*} \quad \left(x+2 \right)^{2}+\left(y-2 \right)^{2}=9 \end{align*}中心間の距離を求めるには、平面上の2点間の距離の公式を用います。
平面上の2点間の距離 1⃣
座標平面上の $2$ 点 $A \ (x_{1} \ , y_{1}) \ , \ B \ (x_{2} \ , \ y_{2})$ 間の距離 $AB$ は
\begin{align*} \quad AB=\sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2} } \end{align*}例題(2)の解答・解説
例題(2)
$2$ つの円 $x^{2}+y^{2}=r^{2} \ (r \gt 0)$ … ①,$x^{2}+y^{2}-8x-4y+15=0$ … ②が共有点をもつような $r$ の値の範囲を求めよ。
例題(2)では、2つの円が共有点をもつ場合を考えます。このとき、共有点は1個または2個です。
共有点を1個もつとき、2つの円が外接するときだけでなく、内接するときもあるので気を付けましょう。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とすると
$(1) \ 2$ つの円が外接する
\begin{align*} \quad d=r+r’ \end{align*}$(2) \ 2$ つの円が内接するか、一致する場合
\begin{align*} \quad d=\left| r-r’ \right| \end{align*}$(1) \ , \ (2)$ を合わせて、$2$ つの円が共有点をもつ場合
\begin{align*} \quad \left| r-r’ \right| \leqq d \leqq r+r’ \end{align*}例題(1)と同様にして、円②の方程式を変形して、中心と半径を求めます。
例題(2)の解答例 1⃣
円①の中心は点 $(0 \ , \ 0)$ で半径は $r$ である。
また、円②の方程式を変形すると
\begin{align*} &\quad x^{2}+y^{2}-8x-4y+15=0 \\[ 7pt ] &\quad \left(x-4 \right)^{2}+\left(y-2 \right)^{2}=5 \end{align*}となるので、中心は点 $(4 \ , \ 2)$ で半径は $\sqrt{5}$ である。
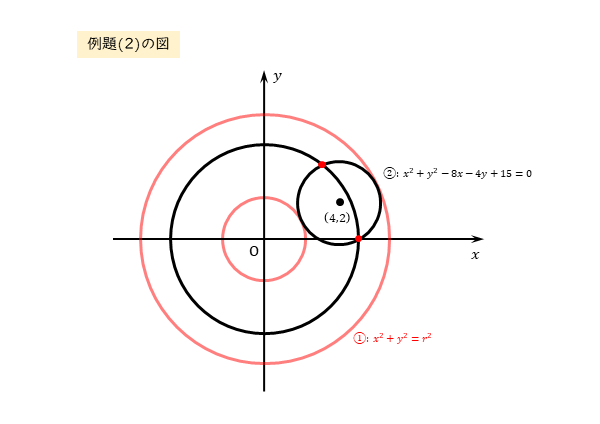
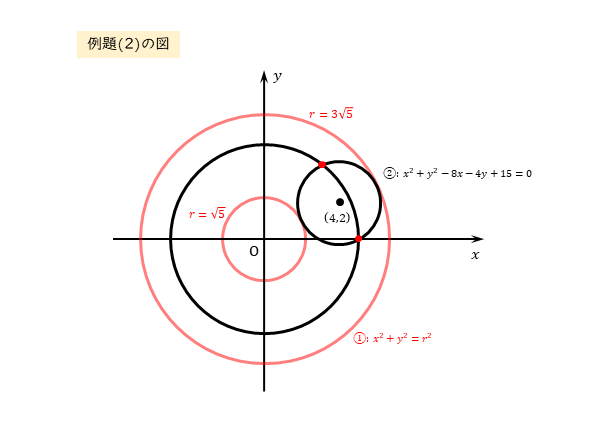
2つの円の中心と半径がそれぞれ分かったので作図しておきます。
2つの円が共有点をもつ状況をイメージできるように、円①を複数描いておくとよいでしょう。
ここでは、外接するとき、共有点を2個もつとき、内接するときの3パターンを描いています。
図から、2つの円が共有点をもつのは、内接するときから外接するときまでだということが分かります。
2つの円の中心間の距離を求めます。
例題(2)の解答例 2⃣
$2$ つの円の中心間の距離は
\begin{align*} \quad \sqrt{ 4^{2} + 2^{2} } &= \sqrt{ 20 } \\[ 7pt ] &= 2 \sqrt{ 5 } \end{align*}2つの円の半径と中心間の距離が揃ったので、2つの円が共有点をもつときの関係式を利用して、半径rについての不等式を導出します。
例題(2)の解答例 3⃣
$2$ つの円①,②が共有点をもつ条件は
\begin{align*} \quad \left| r-\sqrt{ 5 } \right| \leqq 2\sqrt{ 5 } \leqq r+\sqrt{ 5 } \end{align*}$\left| r-\sqrt{ 5 } \right| \leqq 2\sqrt{ 5 }$ から
\begin{align*} \quad -2\sqrt{ 5 } \leqq r-\sqrt{ 5 } \leqq 2\sqrt{ 5 } \end{align*}よって
\begin{align*} \quad -\sqrt{ 5 } \leqq r \leqq 3\sqrt{ 5 } \ \cdots \ \text{③} \end{align*}$2\sqrt{ 5 } \leqq r+\sqrt{ 5 }$ から
\begin{align*} \quad \sqrt{ 5 } \leqq r \ \cdots \ \text{④} \end{align*}③,④と $r \gt 0$ から共通範囲を求めると
\begin{align*} \quad \sqrt{ 5 } \leqq r \leqq 3\sqrt{ 5 } \end{align*}不等式を解くとき、絶対値の扱いに注意しましょう。解答例3⃣では、絶対値を含む不等式の基本形を利用して解きましょう。
絶対値を含む不等式の基本形とその解
$k \gt 0$( $k$ は定数)であるとき
\begin{align*} \quad \left| x \right| \geqq k \end{align*}の解は
\begin{align*} \quad x \leqq -k \ , \ k \leqq x \end{align*}また
\begin{align*} \quad \left| x \right| \leqq k \end{align*}の解は
\begin{align*} \quad -k \leqq x \leqq k \end{align*}また、解答例2⃣において、2点間の距離を求めるとき、一方が原点であれば以下の公式を利用します。
平面上の2点間の距離 2⃣
座標平面上の $2$ 点 $O \ (0 \ , \ 0) \ , \ B \ (x_{1} \ , \ y_{1})$ 間の距離 $OA$ は
\begin{align*} \quad OA=\sqrt{ {x_{1}}^{2}+{y_{1}}^{2} } \end{align*}2つの円の位置関係を調べるときのポイント
2つの円の位置関係を調べるにあたって、注意しなければならない事柄を確認しておきましょう。
2つの円の位置関係を調べるときのポイント
- 2つの円の中心と半径が分かっているか
- 中心間の距離が分かっているか
- 半径の和と差が分かっているか
- 2つの円の半径と中心間の距離の関係がどうなっているか
例題を見れば分かるように、2つの円のうち一方の円の方程式を求める問題になっています。このとき、一方の円の半径が分かっていません。つまり、この半径を求めるのが解答への鍵になります。
半径を求めるために、「内接(または外接)する」や「共有点をもつ」といった条件が与えられます。この条件から、半径についての方程式を導出できれば解答することができます。
次は、2つの円の位置関係を扱った問題を実際に解いてみましょう。