図形と方程式|円と直線の位置関係について

今回は、円と直線の位置関係について学習しましょう。円と直線の共有点があるかないかを調べれば、円と直線の位置関係が分かります。
このことは、2直線の共有点や2次関数と直線の共有点などでも既に学習しています。グラフの式が変わっただけで、基本的な考え方は変わりません。
ただし、円と直線の位置関係に限っては、点と直線の距離もよく利用します。
円と直線の位置関係
円と直線の位置関係は3パターン
円と直線の位置関係は、共有点の個数によって3つに分類されます。
円と直線の位置関係
- 異なる2点で交わる
- 1点で接する
- 共有点をもたない
共有点の個数を調べる際には、円と直線の方程式を連立させて、xまたはyについての2次方程式を導出します。この2次方程式の判別式の値を調べれば、共有点の個数を知ることができます。
共有点の個数を調べるために、判別式の値を求めるのが基本的な解法ではありますが、2次式と1次式を連立させて式変形しなければなりません。展開や同類項の整理などの式変形がやや煩雑になります。
円と直線の共有点を調べるときには、円の中心と直線との距離を求めた方が計算量が少なくて済みます。ですから、円と直線の関係では、点と直線の距離がよく利用されます。
点と直線の距離
点 $(x_{1} \ , \ y_{1})$ と直線 $ax+by+c=0$ の距離 $d$ は
\begin{align*} \quad d=\frac{| ax_{1}+by_{1}+c |}{\sqrt{a^{2}+b^{2}}} \end{align*}ここでは、円と直線の位置関係と共有点の個数だけでなく、円の中心と直線の距離と、円の半径を比較します。これらの関係を関連付けて覚えておきましょう。
円と直線の位置関係 ⇔ 円と直線の共有点の個数 ⇔ 中心と直線の距離と円の半径の大小関係
円と直線が異なる2点で交わるとき
円と直線が異なる2点で交わるときを考えます。円と直線が異なる2点で交わることから、円と直線は共有点を2個もちます。これは図形的に見たときの表現です。
式の面から見ると、円と直線の方程式から導出される2次方程式は、異なる2つの実数解をもちます。また、2次方程式の判別式の値は正(D>0)となります。
これらは図形を見ているのか、方程式を見ているのかの違いだけですべて等価です。
円と直線が異なる2点で交わる
=円と直線が共有点を2個もつ
=2次方程式が異なる2つの実数解をもつ
=2次方程式の判別式の値は正(D>0)
円の中心と直線の距離と円の半径との関係を考えます。円と直線が異なる2点で交わるとき、中心と直線の距離は円の半径よりも小さくなります。
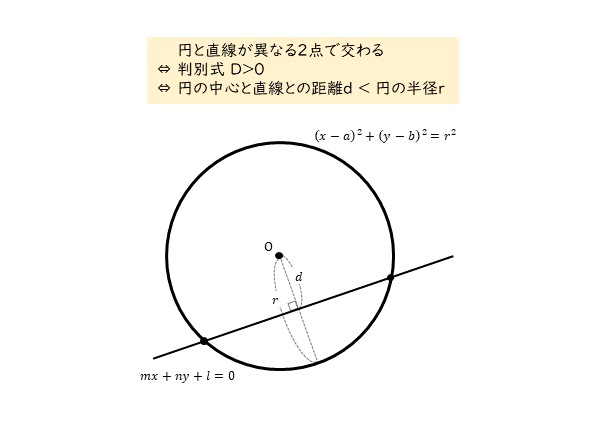
円と直線が異なる2点で交わるための条件をまとめると以下のようになります。
円と直線が異なる2点で交わる(=円と直線が共有点を2個もつ)
⇔ 2次方程式の判別式の値は正(D>0)(=2次方程式が異なる2つの実数解をもつ)
⇔ 円の中心と直線の距離dと円の半径rの大小関係はd<r
円と直線が1点で接するとき
円と直線が1点で接するときを考えます。円と直線が1点で接することから、円と直線は共有点を1個もちます。
このとき、円と直線の方程式から導出される2次方程式は、1つの実数解(重解)をもちます。また、2次方程式の判別式の値は0(D=0)となります。もちろん、これらもすべて等価です。
円と直線が1点で接する
=円と直線が共有点を1個もつ
=2次方程式が1つの実数解(重解)をもつ
=2次方程式の判別式の値は0(D=0)
円の中心と直線の距離と円の半径との関係を考えます。円と直線が1点で接するとき、中心と直線の距離は円の半径に等しくなります。
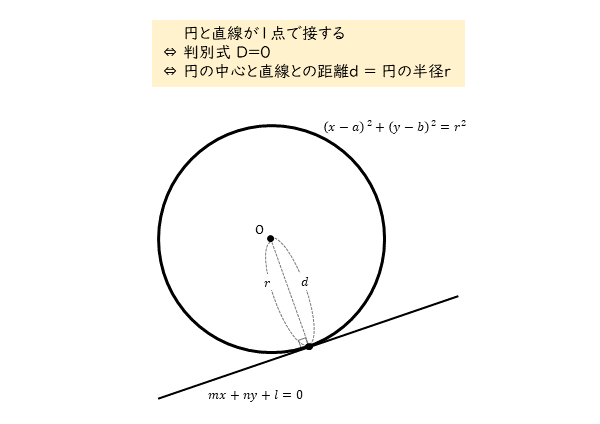
円と直線が1点で接するための条件をまとめると以下のようになります。
円と直線が1点で接する(=円と直線が共有点を1個もつ)
⇔ 2次方程式の判別式の値は0(D=0)(=2次方程式が異なる1つの実数解(重解)をもつ)
⇔ 円の中心と直線の距離dと円の半径rの大小関係はd=r
円と直線が交わらないとき
円と直線が交わらないときを考えます。円と直線が交わらないことから、円と直線は共有点をもちません。
このとき、円と直線の方程式から導出される2次方程式は、実数解をもちません。また、2次方程式の判別式の値は負(D<0)となります。もちろん、これらはすべて等価です。
円と直線が交わらない
=円と直線が共有点をもたない
=2次方程式が実数解をもたない
=2次方程式の判別式の値は負(D<0)
円の中心と直線の距離と円の半径との関係を考えます。円と直線が交わらないとき、中心と直線の距離は円の半径よりも大きくなります。
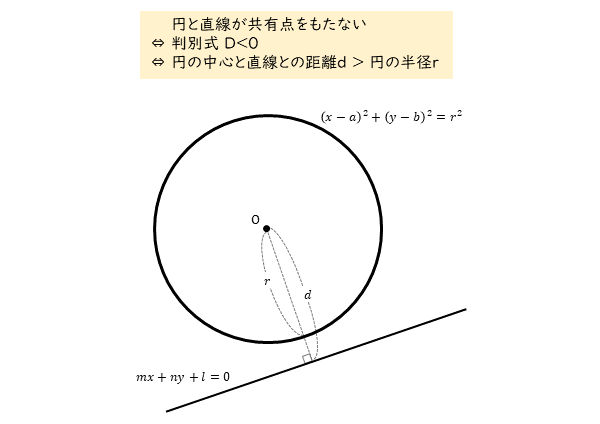
円と直線が交わらないための条件をまとめると以下のようになります。
円と直線が交わらない(=円と直線が共有点をもたない)
⇔ 2次方程式の判別式の値は負(D<0)(=2次方程式が実数解をもたない)
⇔ 円の中心と直線の距離dと円の半径rの大小関係はd>r
以上を踏まえて、例題を解いてみましょう。
例題を解いてみよう
例題
\begin{align*} &\text{円} \ x^{\scriptsize{2}}+2x+y^{\scriptsize{2}}=1 \ \cdots \text{①} \\[ 7pt ] &\text{直線} \ y=mx-m \ \cdots \text{②} \end{align*}円①と直線②が異なる2点で交わるような、定数 $m$ の値の範囲を求めよ。
例題では、円と直線が異なる2点で交わることが条件となっています。この条件を満たす定数mの値の範囲を求めます。
例題の解答・解説
円の方程式は一般形で表されているので、基本形に変形しましょう。すると、円の中心と半径を知ることができます。これで円を図示することができます。
一般形から基本形へ
\begin{align*} \quad x^{2}+2x+y^{2}=1 \ \cdots \text{①} \end{align*}円①の方程式を変形すると
\begin{align*} &\quad \left(x+1 \right)^{2}-1+y^{2}=1 \\[ 7pt ] &\quad \left(x+1 \right)^{2}+y^{2}=2 \end{align*}これより、円の中心は
\begin{align*} \quad ( -1 \ , \ 0 ) \end{align*}円の半径は
\begin{align*} \quad \sqrt{2} \end{align*}また、直線の方程式には定数mが含まれます。ですから、直線を図示することは難しそうです。
しかし、定数mについて整理して、恒等式の性質を利用すれば、定数mの値にかかわらず直線が通る定点の座標が分かります。この定点の座標が分かれば、だいぶまともな作図になります。
直線②が通る定点を調べる
\begin{align*} \quad y=mx-m \ \cdots \text{②} \end{align*}直線②の方程式を $m$ について整理すると
\begin{align*} \quad m(x-1)-y=0 \end{align*}この等式が $m$ の値にかかわらず成り立つには
\begin{align*} \quad x-1=0 \ \text{かつ} \ y=0 \end{align*}よって
\begin{align*} \quad x=1 \ , \ y=0 \end{align*}したがって、直線②は常に
\begin{align*} \quad (1 \ , \ 0) \end{align*}を通る。
円の中心と半径、直線が通る定点の座標が分かりました。これをもとに作図すると以下のようになります。
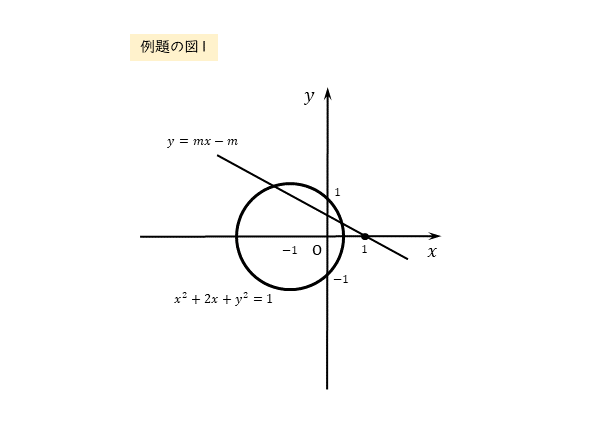
作図すると、たとえば円とy軸の交点の座標などの新しい情報を得ることができます。情報は多いほど良いでしょう。
判別式を利用する解法であれば、上述の作業は正直必要ありません。しかし、入試では図が添付されることは少ないので、図形を扱った問題であれば作図する習慣をつけておいた方が無難です。
問題文に「値の範囲」とあるので、不等式を導出すれば良いことが分かります。共有点の個数と不等式が出てくれば、判別式です。そのために円と直線の方程式から2次方程式を導出します。
例題の解答例 1⃣
\begin{align*} &\text{円} \ x^{2}+2x+y^{2}=1 \ \cdots \text{①} \\[ 7pt ] &\text{直線} \ y=mx-m \ \cdots \text{②} \end{align*}②を①に代入して整理すると
\begin{align*} &\quad x^{2}+2x+\left( mx-m \right)^{2}=1 \\[ 7pt ] &\quad \left( m^{2}+1 \right)x^{2}-2\left( m^{2}-1 \right)x+m^{2}-1=0 \end{align*}文字xについての2次方程式を導出できました。次に、2次方程式の判別式を導出します。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left( m^{2}+1 \right)x^{2}-2\left( m^{2}-1 \right)x+m^{2}-1=0 \end{align*}判別式を $D$ とすると
\begin{align*} \quad \frac{D}{4}=\bigl\{-\left(m^{2}-1 \right) \bigr\}^{2}-\left( m^{2}+1 \right) \left( m^{2}-1 \right) \end{align*}整理すると
\begin{align*} \quad \frac{D}{4} &=\left(m^{2}-1 \right)^{2}-\left( m^{2}+1 \right) \left( m^{2}-1 \right) \\[ 7pt ] &=\left(m^{2}-1 \right) \bigl\{ \left(m^{2}-1 \right)-\left( m^{2}+1 \right) \bigr\} \\[ 7pt ] &=-2\left(m^{2}-1 \right) \\[ 7pt ] &=-2\left(m+1 \right) \left(m-1 \right) \end{align*}判別式の変形では、素直に展開すると4次式になるので、共通因数でくくって因数分解しています。必ず展開しなければならないわけではないので、工夫して変形しましょう。
判別式の値が正であれば、2次方程式が異なる2つの実数解をもちます。このとき、円と直線は共有点を2個もつ、言い換えると円と直線は異なる2点で交わります。
判別式の値が正であることを条件にして、定数mについての不等式を導出します。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{D}{4}=-2\left(m+1 \right) \left(m-1 \right) \end{align*}円①と直線②が異なる $2$ 点で交わるための条件は
\begin{align*} \quad D \gt 0 \end{align*}であるので
\begin{align*} \quad -2\left(m+1 \right) \left(m-1 \right) \gt 0 \end{align*}より
\begin{align*} \quad \left(m+1 \right) \left(m-1 \right) \lt 0 \end{align*}よって
\begin{align*} \quad -1 \lt m \lt 1 \end{align*}得られた定数mの値の範囲が、判別式の値が正であるときの範囲です。判別式を利用した解法であれば、作図なしでも解くことができます。
ちなみに、定数mの値が求めた範囲内にあるとき、円と異なる2点で交わる直線は、2つの接線の間を通ります。
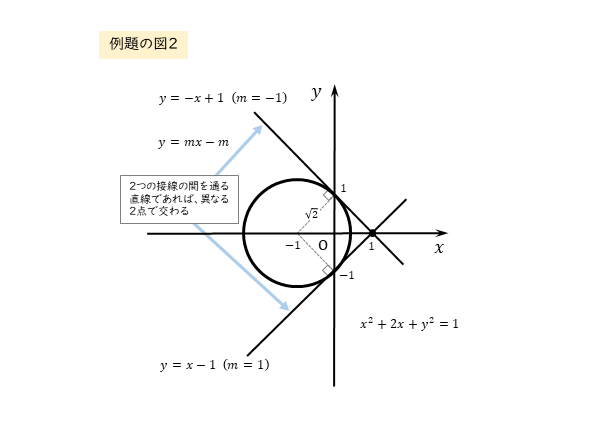
作図してみると、求める範囲が閉じた範囲かどうかも予測できます。
例題の別解
別解は、円の中心と直線の距離と円の半径の大小関係を利用して求める解法です。
円の中心と半径が必要なので、円の方程式を一般形から基本形に変形します(すでに上述済み)。
例題の別解例 1⃣
\begin{align*} \quad x^{2}+2x+y^{2}=1 \ \cdots \text{①} \end{align*}①を変形すると
\begin{align*} &\quad \left(x+1 \right)^{2}-1+y^{2}=1 \\[ 7pt ] &\quad \left(x+1 \right)^{2}+y^{2}=2 \end{align*}よって、円の中心は
\begin{align*} \quad ( -1 \ , \ 0 ) \end{align*}また、円の半径は
\begin{align*} \quad \sqrt{2} \end{align*}たとえば、以下のように作図できればイメージが固まるでしょう。
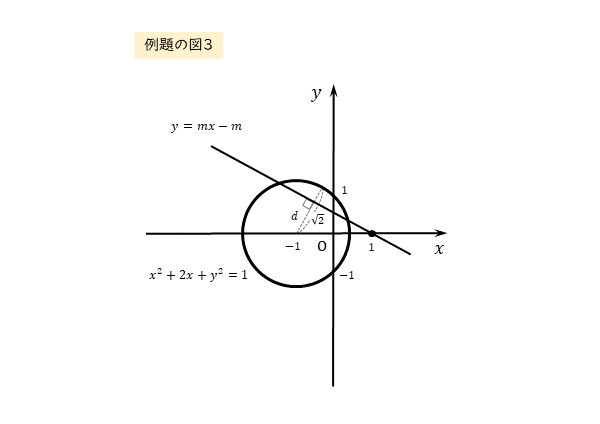
点と直線の距離の公式を利用して、中心と直線の距離を求めます。この距離が半径よりも小さくなれば、円と直線が異なる2点で交わります。図のおかげで、距離と半径の大小関係がはっきりします。
例題の別解例 2⃣
\begin{align*} \quad \vdots \end{align*}②を変形すると
\begin{align*} \quad mx-y-m=0 \end{align*}また、円①の中心と直線②の距離を $d$ とする。
円①と直線②が異なる $2$ 点で交わるための条件は
\begin{align*} \quad d \lt \sqrt{2} \end{align*}距離 $d$ は
\begin{align*} \quad d &=\frac{|m \cdot \left(-1 \right)-0-m|}{\sqrt{m^{2}+\left( -1 \right)^{2}}} \\[ 7pt ] &=\frac{| -2m|}{\sqrt{m^{2}+1}} \\[ 7pt ] &=\frac{2 |m|}{\sqrt{m^{2}+1}} \end{align*}であるので
\begin{align*} \quad \frac{2 |m|}{\sqrt{m^{2}+1}} \lt \sqrt{2} \end{align*}あとは、不等式を変形して、定数mの値の範囲を求めます。
例題の別解例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{2 |m|}{\sqrt{m^{2}+1}} \lt \sqrt{2} \end{align*}ここで
\begin{align*} \quad \sqrt{m^{2}+1} \gt 0 \end{align*}であるので、これを両辺に掛けると
\begin{align*} \quad 2 |m| \lt \sqrt{2} \cdot \sqrt{m^{2}+1} \end{align*}両辺は負ではないので $2$ 乗して
\begin{align*} \quad 4m^{2} \lt 2 \left( m^{2}+1 \right) \end{align*}整理すると
\begin{align*} &\quad 2m^{2} \lt m^{2}+1 \\[ 7pt ] &\quad m^{2}-1 \lt 0 \\[ 7pt ] &\quad \left(m+1 \right) \left(m-1 \right) \lt 0 \end{align*}よって
\begin{align*} \quad -1 \lt m \lt 1 \end{align*}点と直線の距離の公式には絶対値が含まれるので、式変形に注意が必要です。
特に、不等式を扱うので、両辺に掛けるものによっては不等号の向きが変わる可能性があります。掛けるものの正負をきちんと示しておきましょう。
また、不等式の両辺を2乗するときにも注意しましょう。両辺がともに正であれば、両辺を2乗しても不等号の向きは変わりません。
不等式の変形には細心の注意を払おう。
次は、円と直線の位置関係を扱った問題を実際に解いてみましょう。









