図形と方程式|円と直線の位置関係について

円と直線の位置関係を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*} &\text{円} \ x^{2}+y^{2}-4x-6y+9=0 \ \cdots \text{①} \\[ 7pt ] &\text{直線} \ y=kx+2 \ \cdots \text{②} \end{align*}円①と直線②が共有点をもつような、定数 $k$ の値の範囲を求めよ。
問の解答・解説
円と直線が共有点をもつことが条件です。共有点の個数が言及されていません。つまり、共有点は1個でも2個でも良いということです。
例題と同じ要領で解きましょう。円と直線の方程式を連立させて2次方程式を導出します。
問の解答例 1⃣
\begin{align*} &\text{円} \ x^{2}+y^{2}-4x-6y+9=0 \ \cdots \text{①} \\[ 7pt ] &\text{直線} \ y=kx+2 \ \cdots \text{②} \end{align*}②を①に代入して整理すると
\begin{align*} &\quad x^{2}+\left( kx+2 \right)^{2}-4x-6 \left( kx+2 \right)+9=0 \\[ 7pt ] &\quad \left( k^{\scriptsize{2}}+1 \right)x^{\scriptsize{2}}-2\left( k+2 \right)x+1=0 \end{align*}文字xについての2次方程式を導出できました。係数を整理するときにミスがないようにしましょう。
次に、2次方程式の判別式を導出します。
問の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left( k^{2}+1 \right)x^{2}-2\left( k+2 \right)x+1=0 \end{align*}判別式を $D$ とすると
\begin{align*} &\quad \frac{D}{4}=\bigl\{-\left(k+2 \right) \bigr\}^{2}-\left( k^{2}+1 \right) \cdot 1 \end{align*}整理すると
\begin{align*} \quad \frac{D}{4} &=\left(k+2 \right)^{2}-\left( k^{2}+1 \right) \\[ 7pt ] &=4k+3 \end{align*}判別式の値が0以上であれば、2次方程式が重解、または異なる2つの実数解をもちます。このとき、円と直線は共有点を1個または2個もつ、言い換えると円と直線は1点で接する、または異なる2点で交わります。
円と直線が共有点をもつ
=円と直線が共有点を1個、または2個もつ
=2次方程式が1つ、または2つの実数解をもつ
=2次方程式の判別式の値は0以上(D≧0)
判別式の値が0以上であることを条件にして、定数kについての不等式を導出します。
問の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{D}{4}=4k+3 \end{align*}円①と直線②が共有点をもつための条件は
\begin{align*} \quad D \geqq 0 \end{align*}であるので
\begin{align*} \quad 4k+3 \geqq 0 \end{align*}よって
\begin{align*} \quad k \geqq -\frac{3}{4} \end{align*}2次方程式や判別式をミスなく導出できれば、作図なしでも解けます。
問の別解例
別解では、円の中心と直線の距離と円の半径との大小関係を利用します。円の中心と半径が必要なので、円の方程式を一般形から基本形に変形します。
問の別解例 1⃣
\begin{align*} \quad x^{2}+y^{2}-4x-6y+9=0 \ \cdots \text{①} \end{align*}①を変形すると
\begin{align*} &\quad \left(x-2 \right)^{2}-4+\left(y-3 \right)^{2} -9+9=0 \\[ 7pt ] &\quad \left(x-2 \right)^{2}+\left(y-3 \right)^{2}=4 \end{align*}よって、円の中心は
\begin{align*} \quad ( 2 \ , \ 3 ) \end{align*}また、円の半径は
\begin{align*} \quad 2 \end{align*}余談になりますが、作図のために直線が通る定点も調べておきます。定数kについて整理して、恒等式の性質を利用します。
直線②が通る定点を調べる
\begin{align*} \quad y=kx+2 \ \cdots \text{②} \end{align*}直線②の方程式を $k$ について整理すると
\begin{align*} \quad kx+(-y+2)=0 \end{align*}この等式が $k$ の値にかかわらず成り立つには
\begin{align*} \quad x=0 \ \text{かつ} \ -y+2=0 \end{align*}よって
\begin{align*} \quad x=0 \ , \ y=2 \end{align*}したがって、直線②はつねに
\begin{align*} \quad (0 \ , \ 2 ) \end{align*}を通る。
少し堅苦しくなりましたが、この点のy座標は、実は切片です。式から分かるように、切片が一定で傾きが変わるのが直線②です。ですから、直線②は、傾きが変わっても点(0,2)をつねに通ります。
図は以下のようになります。
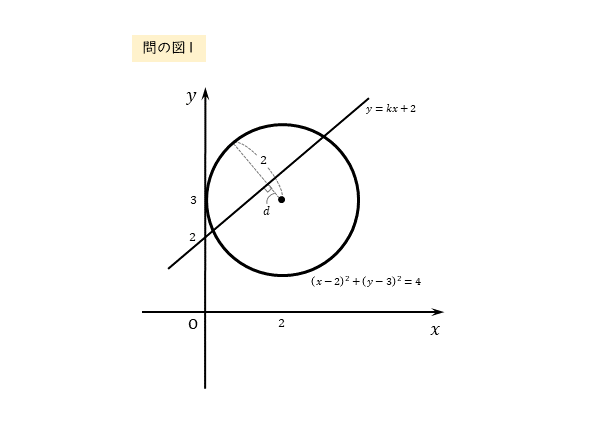
本題に戻ります。点と直線の距離の公式を利用して、中心と直線の距離を求めます。この距離が半径に等しくなるか、あるいは半径よりも小さくなるかすれば、円と直線が共有点をもちます。
問の別解例 2⃣
\begin{align*} \quad \vdots \end{align*}②を変形すると
\begin{align*} \quad kx-y+2=0 \end{align*}また、円①の中心と直線②の距離を $d$ とする。
円①と直線②が共有点をもつための条件は
\begin{align*} \quad d \leqq 2 \end{align*}距離 $d$ は
\begin{align*} \quad d &=\frac{|k \cdot 2-3+2|}{\sqrt{k^{2}+\left( -1 \right)^{2}}} \\[ 7pt ] &=\frac{|2k-1|}{\sqrt{k^{2}+1}} \end{align*}であるので
\begin{align*} \quad \frac{|2k-1|}{\sqrt{k^{2}+1}} \leqq 2 \end{align*}あとは、不等式を変形して、定数kの値の範囲を求めます。
問の別解例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{|2k-1|}{\sqrt{k^{2}+1}} \leqq 2 \end{align*}ここで
\begin{align*} \quad \sqrt{k^{2}+1} \gt 0 \end{align*}であるので、これを両辺に掛けると
\begin{align*} \quad |2k-1| \leqq 2 \cdot \sqrt{k^{2}+1} \end{align*}両辺は負ではないので $2$ 乗して
\begin{align*} \quad \left( 2k-1 \right)^{2} \leqq 4 \left( k^{2}+1 \right) \end{align*}整理すると
\begin{align*} &\quad 4k^{2}-4k+1 \leqq 4k^{2}+4 \\[ 7pt ] &\quad -4k-3 \leqq 0 \end{align*}よって
\begin{align*} \quad k \geqq -\frac{3}{4} \end{align*}不等式の変形では不等号の向きに注意しましょう。両辺に掛けるものの正負も重要です。
定数kの値の範囲が閉じていないのは理由があります。作図すると分かるように、円に接する直線にはy軸があります。
例題のように、円と直線が共有点をもつ範囲は、2つの接線の間になります。ですから、定数kの値の範囲も閉じた範囲になると考えたくなります。
そこで、与えられた直線の式でy軸(x=0)を表すことができるのかを考えてみましょう。
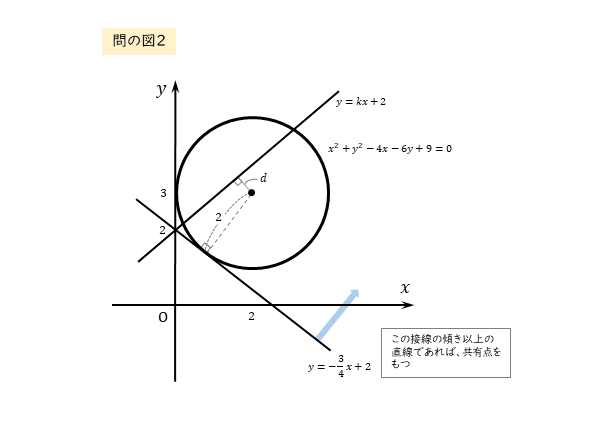
定数kの値を大きくしていくと、直線の傾きが大きくなります。
すると、直線は点(0,2)を中心にして右下がりから右上がりの直線になります。これを続けていくと、直線は徐々にy軸に近づいていきます。
直線がy軸に近づいていきますが、それでもy軸と重なることはありません。それに加えて、定数kの値をどこまで大きくして良いか言えないので、定数kの最大値を決めることができません。
ですから、定数kの値の範囲は閉じた範囲にならず、最小値以上であれば良いということになります。
与えられた直線の式y=kx+2では、どんなに頑張ってもy軸(x=0)を表すことはできない。
Recommended books
さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。
難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。
傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。
◆特長◆大学入試の基本となる問題を扱った問題集です。問題数は138問です。問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。問題編冊子44頁、解答編冊子224頁の構成となっています。◆自分にあったレベルが選べる!◆
- 基礎レベル
- 共通テストレベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
ここで紹介する問題集は、『大学入試 全レベル問題集 数学』シリーズです。昔からある有名なレベル別問題集です。
3年の1学期までに基礎レベル1を解いて、教科書内容の補完をしてしまいましょう。夏休みになったら、共通テストレベル2で実戦練習をこなすと良いでしょう。9月~10月くらいまでにこの2冊を何度も周回して仕上げれば、秋からの2次対策にスムーズに移行できるでしょう。
なお、新入試に対応するための改訂版が2020年2月に出版されています。改訂版を希望する場合、「新入試対応」とあるものを購入しましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 円と直線の位置関係は3パターン。
- 作図して円と直線の位置関係を把握しよう。
- 円と直線の位置関係は直線が円に接するときを考えよう。
- 円と直線の共有点の個数は、円と直線の方程式から得た2次方程式の判別式の値で決まる。
- 円の中心と直線の距離と円の半径との大小関係でも良い。計算の負担が比較的少ない。












