図形と方程式｜円と直線の共有点の座標について

01/08/2023数学２

今回は、円と直線の共有点の座標について学習しましょう。グラフの共有点はこれまでにも扱っています。たとえば、２直線の共有点や２次関数と直線の共有点などです。

グラフの式が変わっただけで、基本的な考え方は変わりません。

円周上や直線上の点

円周上にある点や、直線上にある点の座標は、それぞれの方程式を満たす解です。ですから、円や直線の方程式を満たさないものは、グラフ上の点ではありません。

円と直線の共有点とは、円周上にあって、なおかつ直線上にもある点のことです。したがって、円と直線の共有点の座標は、円の方程式を満たし、なおかつ直線の方程式も満たすことになります。

このような共有点の座標を求めるには、円と直線の方程式を連立させて解きます。

連立方程式の解は、それぞれの方程式を満たす解。

共有点があるとき、連立方程式を解くと実数解が得られます。

それに対して、共有点がないとき、連立方程式を解いても実数解が得られません。計算ミスがなくても実数解が出てこない場合があるので注意しましょう。

例題で手順を確認してみましょう。

円と直線の座標を求めてみよう

円と直線の座標を求めてみましょう。

例題

円 $x^{2}+y^{2}=5$ … ① と次の直線に共有点はあるか。あるときは、その点の座標を求めよ。

$(1) \ y=x+1$

$(2) \ y=-2x+5$

$(3) \ y=2x-6$

２次式と１次式を連立させて解くので、加減法ではなく、代入法を利用しましょう。

例題(1)の解答・解説

例題(1)

円 $x^{2}+y^{2}=5$ … ① と次の直線に共有点はあるか。あるときは、その点の座標を求めよ。

$y=x+1$

作図すればおおよその関係が掴めます。

答案を作成する前に、しっかりと作図しておきましょう。

円と直線の共有点は第１象限と第３象限にできそうです。

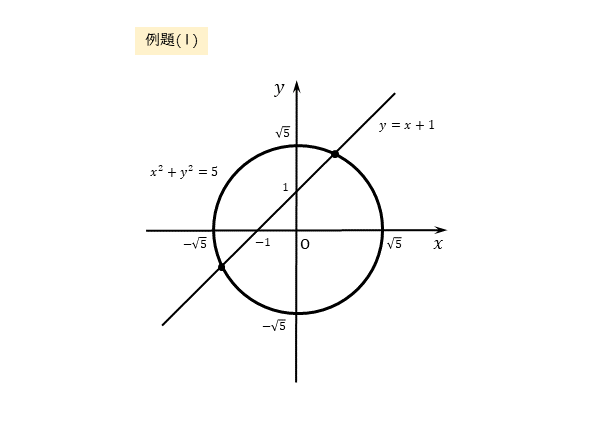
円と直線の方程式を連立させて解きます。

例題(1)の解答例 1⃣

$y=x+1$ … ②を①に代入して整理すると

$\begin{align*} &\quad x^{2}+\left( x+1 \right)^{2}=5 \\[ 7pt ] &\quad x^{2}+x^{2}+2x+1=5 \\[ 7pt ] &\quad 2x^{2}+2x-4=0 \\[ 7pt ] &\quad x^{2}+x-2=0 \\[ 7pt ] &\quad \left( x+2 \right)\left( x-1 \right)=0 \end{align*}$

これを解くと

$\begin{align*} \quad x=-2 \ , \ 1 \end{align*}$

円と直線の方程式を連立させて解くと、文字ｘについての２次方程式を導けます。そして、この２次方程式を解くと、共有点があれば実数解が得られます。

実数解は共有点のｘ座標です。例題(1)では、実数解が２個得られたので、共有点は２個あることが分かります。実数解と見比べてみても、作図は間違ってなさそうです。

実数解の個数は、共有点の個数に対応する。

共有点のｙ座標を求めます。得られた実数解と直線の方程式を利用しましょう。

例題(1)の解答例 2⃣

$y=x+1$ … ②を①に代入して整理すると

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x=-2 \ , \ 1 \end{align*}$

これを②に代入すると

$x=-2$ のとき

$\begin{align*} \quad y=-1 \end{align*}$

$x=1$ のとき

$\begin{align*} \quad y=2 \end{align*}$

よって、円①と直線②は

$\begin{align*} \quad ( -2 \ , \ -1 ) \ , \ ( 1 \ , \ 2 ) \end{align*}$

の $2$ 点で交わる。

連立方程式や２次方程式についての知識があれば、円と直線の共有点の座標を求めることができます。

円と直線の共有点の座標 ⇔ 連立方程式の実数解

例題(2)の解答・解説

例題(2)

円 $x^{2}+y^{2}=5$ … ① と次の直線に共有点はあるか。あるときは、その点の座標を求めよ。

$y=-2x+5$

例題(2)の作図については、少し注意する必要があります。

共有点の有無は解けばはっきりしますが、作図することで、図から円と直線が接する可能性に気付けるかもしれません。

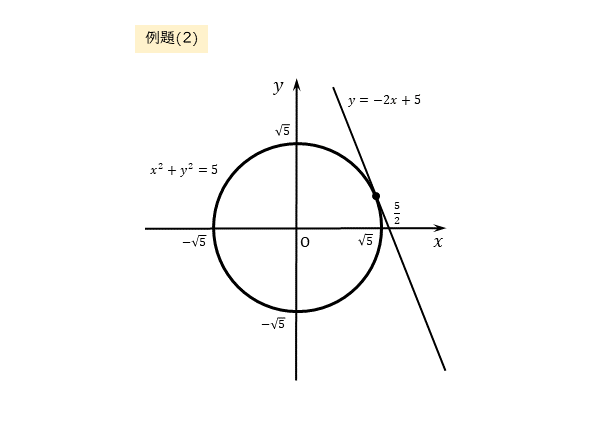
例題(2)も同様にして、円と直線の方程式を連立させて解きます。

例題(2)の解答例 1⃣

$y=-2x+5$ … ③を①に代入して整理すると

$\begin{align*} &\quad x^{2}+\left( -2x+5 \right)^{2}=5 \\[ 7pt ] &\quad x^{2}+4x^{2}-20x+25=5 \\[ 7pt ] &\quad 5x^{2}-20x+20=0 \\[ 7pt ] &\quad x^{2}-4x+4=0 \\[ 7pt ] &\quad \left( x-2 \right)^{2}=0 \end{align*}$

これを解くと

$\begin{align*} \quad x=2 \ \text{（重解）} \end{align*}$

得られた２次方程式を解くと、実数解は重解となりました。

例題(2)では、実数解が１個得られたので、共有点は１個あることが分かります。

共有点のｙ座標を求めます。得られた実数解を直線の方程式に代入します。

例題(2)の解答例 2⃣

$y=-2x+5$ … ③を①に代入して整理すると

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x=2 \ \text{（重解）} \end{align*}$

これを③に代入すると

$\begin{align*} \quad y=1 \end{align*}$

よって、円①と直線③は

$\begin{align*} \quad ( 2 \ , \ 1 ) \end{align*}$

で接する。

円と直線が接する ⇔ 連立方程式の実数解は重解

例題(3)の解答・解説

例題(3)

円 $x^{2}+y^{2}=5$ … ① と次の直線に共有点はあるか。あるときは、その点の座標を求めよ。

$y=2x-6$

例題(3)の作図も注意が必要です。

共有点の有無はまだ不明ですが、図から円と直線が共有点をもたない可能性に気付けるかもしれません。

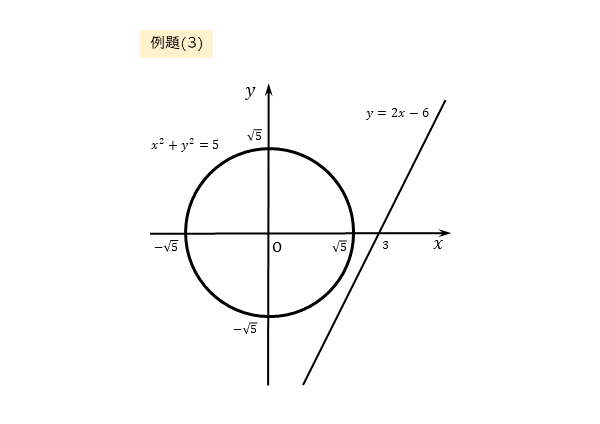
円と直線の方程式を連立させ、文字ｘについての２次方程式を導きます。

例題(3)の解答例 1⃣

$y=2x-6$ … ④を①に代入して整理すると

$\begin{align*} &\quad x^{2}+\left( 2x-6 \right)^{2}=5 \\[ 7pt ] &\quad x^{2}+4x^{2}-24x+36=5 \\[ 7pt ] &\quad 5x^{2}-24x+31=0 \end{align*}$

予め作図していれば共有点がない可能性に気付くので、むやみに２次方程式を解くことはないでしょう。

共有点がなければ２次方程式は実数解をもたないので、実数の範囲では方程式を解くことはできません。導出した２次方程式を見れば、因数分解できそうにないことが分かります。

作図から共有点がない可能性に気付いたり、２次方程式を因数分解できそうにないと感じたりしたら、２次方程式の判別式の値を確認しましょう。

判別式の値が負（Ｄ＞０）であれば、２次方程式は実数解をもちません。２次方程式を解く必要がなくなるので、解が求まらなくて慌てずに済みます。

例題(3)の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 5x^{2}-24x+31=0 \end{align*}$

この $2$ 次方程式の判別式を $D$ とすると

$\begin{align*} \quad \frac{D}{4} &=(-12)^{2}-5 \cdot 31 \\[ 7pt ] &= -11 \lt 0 \end{align*}$

よって、円①と直線④は共有点をもたない。

作図をしていれば、このような解き方が可能になります。共有点の有無で方針が変わるので、解く前に作図する習慣をつけましょう。

実数解をもたない ⇔ 共有点がない

次は、円と直線の共有点の座標を扱った問題を実際に解いてみましょう。

数学２円,共有点,直線,図形と方程式

Posted by kiri

図形と方程式｜円と直線の位置関係について

図形と方程式｜円の方程式の決定について