図形と方程式|円と直線の共有点の座標について

円と直線の共有点の座標を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
次の円と直線に共有点はあるか。あるときは、その点の座標を求めよ。
$(1) \ x^{2}+y^{2}=1 \ , \ x-y=1$
$(2) \ x^{2}+y^{2}=4 \ , \ x+y=3$
$(3) \ x^{2}+y^{2}=2 \ , \ 2x-y=1$
$(4) \ x^{2}+y^{2}=5 \ , \ x-2y=5$
問(1)の解答・解説
問(1)
次の円と直線に共有点はあるか。あるときは、その点の座標を求めよ。
$x^{2}+y^{2}=1 \ , \ x-y=1$
作図は以下の通りです。図から共有点は2個ありそうです。
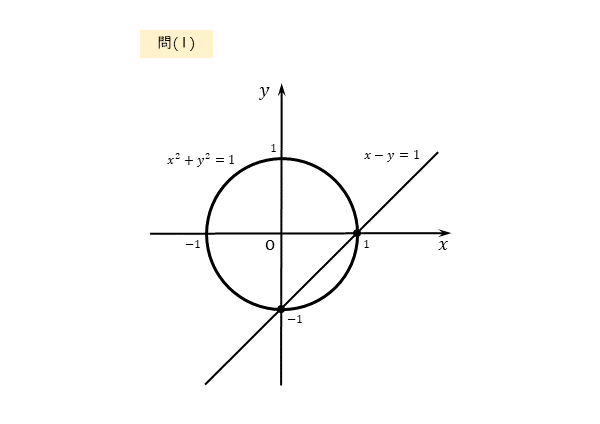
例題と同じ要領で解きましょう。円と直線の方程式を連立させて解きます。
問(1)の解答例 1⃣
\begin{align*} &\quad x^{2}+y^{2}=1 \ \cdots \text{①} \\[ 7pt ] &\quad x-y=1 \ \cdots \text{②} \end{align*}とする。②より
\begin{align*} \quad y=x-1 \ \cdots \text{③} \end{align*}③を①に代入して整理すると
\begin{align*} &\quad x^{2}+\left( x-1 \right)^{2}=1 \\[ 7pt ] &\quad 2x^{2}-2x+1=1 \\[ 7pt ] &\quad x^{2}-x=0 \\[ 7pt ] &\quad x \left( x-1 \right)=0 \end{align*}これを解くと
\begin{align*} \quad x=0 \ , \ 1 \end{align*}実数解が2個なので、共有点は2個あります。
得られた実数解を③式にそれぞれ代入して、共有点のy座標を求めます。
問(1)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=x-1 \ \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad x=0 \ , \ 1 \end{align*}これを③に代入すると
$x=0$ のとき
\begin{align*} \quad y=-1 \end{align*}$x=1$ のとき
\begin{align*} \quad y=0 \end{align*}よって、円と直線は
\begin{align*} \quad ( 0 \ , \ -1 ) \ , \ ( 1 \ , \ 0 ) \end{align*}の $2$ 点で交わる。
作図の段階で共有点の座標が分かることはほとんどないので、共有点の個数が予測できれば良いでしょう。
2次方程式が異なる2つの実数解をもてば、共有点は2個
問(2)の解答・解説
問(2)
次の円と直線に共有点はあるか。あるときは、その点の座標を求めよ。
$x^{2}+y^{2}=4 \ , \ x+y=3$
作図は以下の通りです。図から円と直線が共有点をもたない可能性があります。

円と直線の方程式を連立させて解きます。異なる式に同じ番号を振ることは基本的にしませんが、ここでは便宜上、同じ番号を使うので注意しましょう。
問(2)の解答例 1⃣
\begin{align*} &\quad x^{2}+y^{2}=4 \ \cdots \text{①} \\[ 7pt ] &\quad x+y=3 \ \cdots \text{②} \end{align*}とする。②より
\begin{align*} \quad y=-x+3 \ \cdots \text{③} \end{align*}③を①に代入して整理すると
\begin{align*} &\quad x^{2}+\left( -x+3 \right)^{2}=4 \\[ 7pt ] &\quad 2x^{2}-6x^{2}+9=4 \\[ 7pt ] &\quad 2x^{2}-6x+5=0 \end{align*}実数解の有無を調べるために、2次方程式の判別式の値を確認します。
問(2)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 2x^{2}-6x+5=0 \end{align*}この $2$ 次方程式の判別式を $D$ とすると
\begin{align*} \quad \frac{D}{4} &=(-3)^{2}-2 \cdot 5 \\[ 7pt ] &= -1 \lt 0 \end{align*}よって、円と直線は共有点をもたない。
2次方程式は実数解をもたないので、作図は間違っていなかったようです。
2次方程式が実数解をもたなければ、共有点はなし
問(3)の解答・解説
問(3)
次の円と直線に共有点はあるか。あるときは、その点の座標を求めよ。
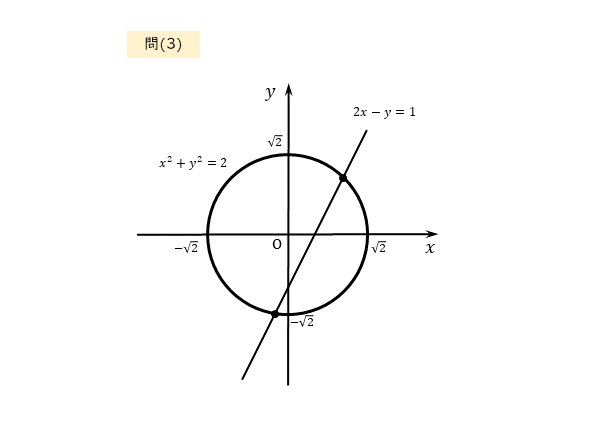
$x^{2}+y^{2}=2 \ , \ 2x-y=1$
作図は以下の通りです。図から共有点は第1象限と第3象限にできそうです。
円と直線の方程式を連立させて解きます。
問(3)の解答例 1⃣
\begin{align*} &\quad x^{2}+y^{2}=2 \ \cdots \text{①} \\[ 7pt ] &\quad 2x-y=1 \ \cdots \text{②} \end{align*}とする。②より
\begin{align*} \quad y=2x-1 \ \cdots \text{③} \end{align*}③を①に代入して整理すると
\begin{align*} &\quad x^{2}+\left( 2x-1 \right)^{2}=2 \\[ 7pt ] &\quad 5x^{2}-4x+1=2 \\[ 7pt ] &\quad 5x^{2}-4x-1=0 \\[ 7pt ] &\quad \left( 5x+1 \right)\left( x-1 \right)=0 \end{align*}これを解くと
\begin{align*} \quad x=-\frac{1}{5} \ , \ 1 \end{align*}実数解が2個なので、共有点は2個あります。
得られた実数解を③式にそれぞれ代入して、共有点のy座標を求めます。
問(3)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=2x-1 \ \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad x=-\frac{1}{5} \ , \ 1 \end{align*}これを③に代入すると
$x=-\frac{1}{5}$ のとき
\begin{align*} \quad y=-\frac{7}{5} \end{align*}$x=1$ のとき
\begin{align*} \quad y=1 \end{align*}よって、円と直線は
\begin{align*} \quad \left( -\frac{1}{5} \ , \ -\frac{7}{5} \right) \ , \ ( 1 \ , \ 1 ) \end{align*}の $2$ 点で交わる。
2次方程式が異なる2つの実数解をもてば、共有点は2個
問(4)の解答・解説
問(4)
次の円と直線に共有点はあるか。あるときは、その点の座標を求めよ。
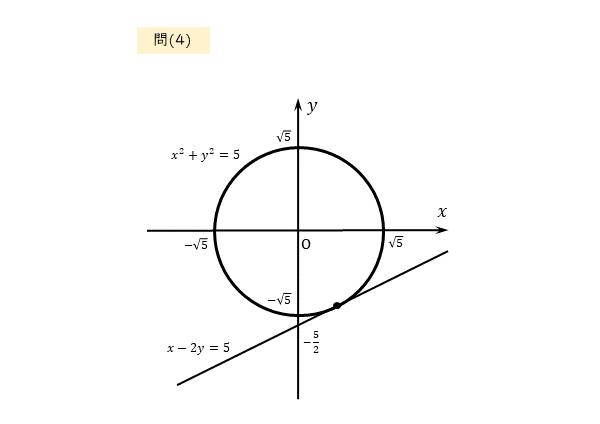
$x^{2}+y^{2}=5 \ , \ x-2y=5$
作図は以下の通りです。図から円と直線が接する可能性があります。
円と直線の方程式を連立させて解きます。代入する式を工夫しましょう。
問(4)の解答例 1⃣
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \text{①} \\[ 7pt ] &\quad x-2y=5 \ \cdots \text{②} \end{align*}とする。②より
\begin{align*} \quad x=2y+5 \ \cdots \text{③} \end{align*}③を①に代入して整理すると
\begin{align*} &\quad \left( 2y+5 \right)^{2}+y^{2}=5 \\[ 7pt ] &\quad 5y^{2}+20y+25=5 \\[ 7pt ] &\quad y^{2}+4y+4=0 \\[ 5pt ] &\quad \left( y+2 \right)^{2}=0 \end{align*}これを解くと
\begin{align*} \quad y=-2 \ \text{(重解)} \end{align*}②式を文字yについて変形すると、分数が出てきます。そうすると、代入後の式変形が難しくなり、計算ミスを起こしやすくなります。計算ミスを防ぐために、文字xについて変形して代入します。
代入法は文字の種類を減らすのが目的。消去するのが必ず文字yである理由はない。
得られた実数解を③式に代入して、共有点のx座標を求めます。
問(4)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x=2y+5 \ \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad y=-2 \ \text{(重解)} \end{align*}これを③に代入すると
\begin{align*} \quad x=1 \end{align*}よって、円と直線は
\begin{align*} \quad ( 1 \ , \ -2 ) \end{align*}で接する。
2次方程式が重解をもてば、共有点は1個(接する)
円や直線など複数のグラフを扱う場合、共有点の座標を求めることが多いです。
直接的に「共有点の座標を求めよ」と指示されなかったとしても、ほとんどの場合、設問を解く上で共有点の情報が必要になります。
グラフの方程式や点の座標を求めることはこの分野では必須なので、きちんとマスターしておきましょう。
Recommended books
さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。
難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。
傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。
◆特長◆大学入試の基本となる問題を扱った問題集です。問題数は138問です。問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。問題編冊子44頁、解答編冊子224頁の構成となっています。◆自分にあったレベルが選べる!◆
- 基礎レベル
- 共通テストレベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
ここで紹介する問題集は、『大学入試 全レベル問題集 数学』シリーズです。昔からある有名なレベル別問題集です。
3年の1学期までに基礎レベル1を解いて、教科書内容の補完をしてしまいましょう。夏休みになったら、共通テストレベル2で実戦練習をこなすと良いでしょう。9月~10月くらいまでにこの2冊を何度も周回して仕上げれば、秋からの2次対策にスムーズに移行できるでしょう。
なお、新入試に対応するための改訂版が2020年2月に出版されています。改訂版を希望する場合、「新入試対応」とあるものを購入しましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 円と直線の共有点の座標は、連立方程式の実数解。
- 連立方程式から代入法で2次方程式を導こう。
- x,yのいずれかについての2次方程式であれば良い。
- 作図して円と直線の位置関係を把握しよう。
- 共有点がなさそうなら、2次方程式の判別式の値を調べよう。
- 判別式の値が負であれば、共有点はない。















