図形と方程式|円の方程式の決定について

今回は、円の方程式の決定について学習しましょう。円の方程式には基本形と一般形があります。どちらの形にするかは問題で与えられた条件に従います。
実は、円の方程式の決定の基本的な事柄については、すでに学習しています。今回はそれよりもやや難易度の高い問題となります。
方程式を決定する際には、作図してイメージを膨らませることも大切です。作図しながら考える習慣をつけておきましょう。
円の方程式の決定
円の方程式に必要な情報
円の方程式を決定する際に、どんな情報を入手すれば良いのかを知っておかなければなりません。
円の方程式に必要な情報は、中心の座標と半径です。この2つが分かれば、円の方程式を基本形で表すことができます。
円の方程式
基本形
中心が $(a \ , \ b)$ で、半径が $r$ の円の方程式
\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}また、原点が中心のとき、$a=0 \ , \ b=0$ より
\begin{align*} \quad x^{2}+y^{2}=r^{2} \end{align*}一般形
\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}問題文を読む際には、円の中心と半径が分かる情報がないかを意識しましょう。必ず何らかの情報が与えられているはずです。
早速、例題を解いてみましょう。
円の方程式を決定してみよう
円の方程式を決定してみましょう。
例題
直線 $y=-4x+5$ 上に中心があり、$x$ 軸と $y$ 軸の両方に接する円の方程式を求めよ。
例題の解答・解説
中心と半径は直接的に与えられていません。自分で求める必要があります。問題文を読み、作図しながら与えられた情報を吟味してみましょう。
中心と半径を求める必要があるので、問題文からきっかけとなる文言を探します。すると、以下のような事柄が分かります。
与えられた情報を吟味する
- 中心が直線y=-4x+5上にある ⇒ 中心の座標を表せる
- x軸とy軸の両方に接する円 ⇒ 中心の座標が半径に利用できる
作図をすると良く分かりますが、条件を満たす円は複数あることが分かります。
作図の結果から、円は第1象限と第4象限にできそうだと推測できます。ここで注意したいのは、第4象限にできる円です。
中心の座標が半径に関わるのは分かりますが、半径は正の値です。座標には負の数もあるので、座標を利用するときには注意が必要です。
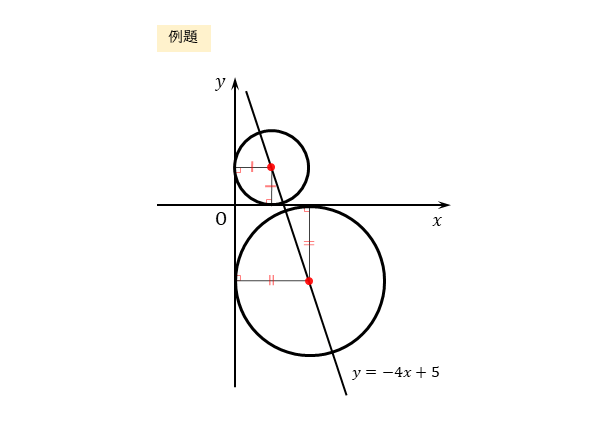
軸に接する円の半径を中心の座標で表せることは学習済みです。しかし、文字が絡むと、正負がよく分からなくなります。ですから、絶対値を上手に利用しましょう。
軸に接する円の半径
- x軸に接する円の半径
- |中心のy座標|=(半径)
- y軸に接する円の半径
- |中心のx座標|=(半径)
例題の場合、x軸とy軸の両方に接するので、中心のx座標とy座標の絶対値は、どちらも半径に等しくなることが分かります。
何はともあれ、半径を表すには、中心の座標がなければ始まりません。中心が直線上にあることを利用して、その座標を表すことができれば半径の方にもつながりそうです。
下図のような状態になっていれば、最後まで解くことができるでしょう。
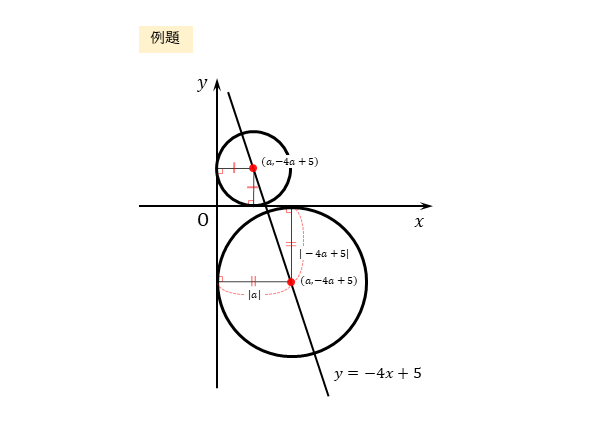
以上のことを踏まえて、解答例は以下のようになります。
例題(1)の解答例 1⃣
円が直線
\begin{align*} \quad y=-4x+5 \end{align*}上にあるので、中心の座標は
\begin{align*} \quad (a \ , \ -4a+5 ) \end{align*}と表される。
また、円が $x$ 軸と $y$ 軸に接するので、円の半径を $r$ とすると
\begin{align*} \quad |a|=|-4a+5|=r \end{align*}となる。
ここまではほとんどの人が記述できるのではないかと思います。問題はこれからで、絶対値の扱い方を知っているかどうかになります。これまでの知識が問われる場面です。
絶対値の扱いに注意しながら、文字aについての方程式を解きます。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad |a|=|-4a+5|=r \end{align*}ここで
\begin{align*} \quad |a|=|-4a+5| \end{align*}より
\begin{align*} \quad a=\pm (-4a+5) \end{align*}$a=-4a+5$ のとき
これを解くと
\begin{align*} \quad a=1 \end{align*}よって、中心の座標は
\begin{align*} \quad (1 \ , \ 1) \end{align*}また
\begin{align*} \quad r=1 \end{align*}$a=-(-4a+5)$ のとき
これを解くと
\begin{align*} \quad a=\frac{5}{3} \end{align*}よって、中心の座標は
\begin{align*} \quad \left(\frac{5}{3} \ , \ -\frac{5}{3} \right) \end{align*}また
\begin{align*} \quad r=\frac{5}{3} \end{align*}したがって、求める円の方程式は
\begin{align*} &\quad \left(x-1 \right)^{2}+\left(y-1 \right)^{2}=1 \\[ 7pt ] &\quad \left(x-\frac{5}{3} \right)^{2}+\left(y+\frac{5}{3} \right)^{2}=\frac{25}{9} \end{align*}中心の座標を自分で設定した後は、絶対値を上手に外すことがポイントでした。中心の座標や半径を基本形に代入するだけの問題と比べると、既習内容の知識も必要なので応用的な問題です。
中心の座標を利用するとは絶対値を忘れないこと。
絶対値の外し方には他にもあります。たとえば、両辺を2乗してしまう方法です。
例題の解答例2⃣の別解
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad |a|=|-4a+5|=r \end{align*}ここで
\begin{align*} \quad |a|=|-4a+5| \end{align*}の両辺を $2$ 乗すると
\begin{align*} \quad a^{2}=(-4a+5)^{2} \end{align*}これを解くと
\begin{align*} &\quad a^{2}=16a^{2}-40a+25 \\[ 7pt ] &\quad 15a^{2}-40a+25=0 \\[ 7pt ] &\quad 3a^{2}-8a+5=0 \\[ 7pt ] &\quad \left( a-1 \right)\left( 3a-5 \right)=0 \\[ 7pt ] &\quad a=1 \ , \ \frac{5}{3} \end{align*}$a=1$ のとき
中心の座標は
\begin{align*} \quad (1 \ , \ 1) \end{align*}また
\begin{align*} \quad r=1 \end{align*}$a=\frac{5}{3}$ のとき
中心の座標は
\begin{align*} \quad \left(\frac{5}{3} \ , \ -\frac{5}{3} \right) \end{align*}また
\begin{align*} \quad r=\frac{5}{3} \end{align*}したがって、求める円の方程式は
\begin{align*} &\quad \left(x-1 \right)^{2}+\left(y-1 \right)^{2}=1 \\[ 7pt ] &\quad \left(x-\frac{5}{3} \right)^{2}+\left(y+\frac{5}{3} \right)^{2}=\frac{25}{9} \end{align*}2次方程式を解く必要があるので、模範解答に比べて式変形がやや煩雑になってしまいます。
次は、円の方程式の決定を扱った問題を実際に解いてみましょう。









