図形と方程式｜円の方程式の一般形と図形について

08/29/2023数学２

今回は、円の方程式の一般形と図形の関係について学習しましょう。円の方程式の基本形を展開したものが一般形です。この一般形が表す図形について出題されることがあります。

一般に、基本形よりも一般形が与えられる場合が多いので、基本形への変形に慣れておきましょう。

円の方程式の基本形と一般形

円の方程式の基本形

円の方程式は、円という図形の性質から導かれます。円は、ある１点からの距離がつねに一定となる点の集まりです。このある１点が円の中心です。

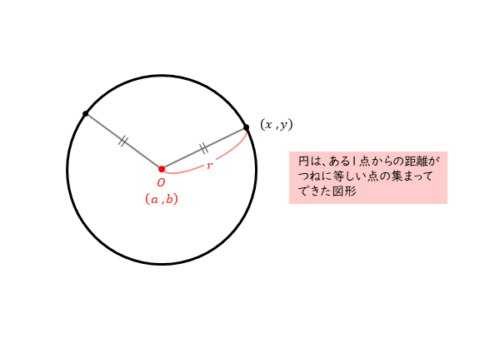
円の方程式（基本形）

中心が $(a \ , \ b)$ で、半径が $r$ の円の方程式

$\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}$

基本形の導出については、前回の記事（図形と方程式｜円の方程式の基本形と一般形について）で解説済みなので、ここでは省略します。特に、原点が中心の場合、基本形は以下のようになります。

円の中心が原点の場合

円の方程式

$\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}$

において、 $a=0 \ , \ b=0$ であるから

$\begin{align*} \quad x^{2}+y^{2}=r^{2} \end{align*}$

円の方程式の一般形

円の方程式の基本形を展開したものが一般形です。

円の方程式(一般形)

円の方程式の一般形は

$\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}$

一般形から基本形への変形の過程は以下のようになります。

一般形から基本形への変形

円の方程式を

$\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}$

とする。

$x \ , \ y$ について平方完成すると

$\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}-\frac{l^{2}}{4}+\left(y+\frac{m}{2} \right)^{2}-\frac{m^{2}}{4}+n=0 \end{align*}$

整理すると

$\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\left(y+\frac{m}{2} \right)^{2}=\frac{l^{2}+m^{2}-4n}{4} \end{align*}$

一般形から基本形に変形すると、方程式が円を表すための条件が分かります。

一般形から基本形に変形して分かること

$\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\left(y+\frac{m}{2} \right)^{2}=\frac{l^{2}+m^{2}-4n}{4} \end{align*}$

$l^{2}+m^{2}-4n \gt 0$ のとき

$\begin{align*} \quad \text{中心} \ \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \ , \ \text{半径} \ \frac{\sqrt{l^{2}+m^{2}-4n}}{2} \end{align*}$

$l^{2}+m^{2}-4n = 0$ のとき

$\begin{align*} \quad \text{円は点} \ \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \ \text{を表す} \end{align*}$

$l^{2}+m^{2}-4n \lt 0$ のとき

$\begin{align*} \quad \text{表す図形はない} \end{align*}$

方程式が円を表すには、上の①の場合でなければなりません。

一般形が円を表すための条件

方程式

$\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}$

が円の方程式となるには

$\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\left(y+\frac{m}{2} \right)^{2}=\frac{l^{2}+m^{2}-4n}{4} \end{align*}$

より

$\begin{align*} \quad l^{2}+m^{2}-4n \gt 0 \end{align*}$

を満たせばよい。

このとき

$\begin{align*} &\quad \text{中心} \quad \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \\[ 7pt ] &\quad \text{半径} \quad \frac{\sqrt{l^{2}+m^{2}-4n}}{2} \end{align*}$

の円を表す。

一般形から基本形に変形できることを優先しましょう。変形できるようになったら、上述の条件を用いて基本形を導くと良いでしょう。

一般形を変形してみよう

一般形で与えられた方程式を変形し、その方程式の表す図形を考えてみましょう。

例題

$(1)$ 方程式 $x^{2}+y^{2}+6x-8y+9=0$ はどんな図形を表すか。

$(2)$ 方程式 $x^{2}+y^{2}+2px+3py+13=0$ が円を表すとき、定数 $p$ の値の範囲を求めよ。

一般形から基本形への変形では平方完成を利用しましょう。

例題(1)の解答・解説

例題(1)

方程式 $x^{2}+y^{2}+6x-8y+9=0$ はどんな図形を表すか。

例題(1)の方程式には、文字ｘ，ｙについて２次の項がそれぞれあります。これらから円の方程式だろうと推測できます。推測通りなのかを実際に変形して確かめましょう。

例題(1)の解答例

与式より

$\begin{align*} &\quad x^{2}+y^{2}+6x-8y+9=0 \\[ 7pt ] &\quad \left( x^{2}+6x+9 \right)-9+\left( y^{2}-8y+16 \right)-16+9=0 \\[ 7pt ] &\quad \left( x+3 \right)^{2}+\left( y-4 \right)^{2}=16 \end{align*}$

よって

$\begin{align*} &\quad \text{中心} \quad (-3 \ , \ 4 ) \\[ 7pt ] &\quad \text{半径} \quad 4 \end{align*}$

の円を表す。

方程式が円を表すときの条件から求めることもできます。この解法は、マーク形式の問題で効果的です。

方程式が円を表すための条件

方程式

$\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}$

が

$\begin{align*} \quad l^{2}+m^{2}-4n \gt 0 \end{align*}$

を満たすとき

$\begin{align*} &\quad \text{中心} \quad \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \\[ 7pt ] &\quad \text{半径} \quad \frac{\sqrt{l^{2}+m^{2}-4n}}{2} \end{align*}$

の円を表す。

これを用いて例題(1)を解いてみましょう。

例題(1)の別解例

与式より

$\begin{align*} &\quad 6^{2}+\left( -8 \right)^{2}-4 \cdot 9 \\[ 7pt ] &=36+64-36 \\[ 7pt ] &=64 > 0 \end{align*}$

より、方程式は円を表す。

このとき、中心の座標は

$\begin{align*} &\quad -\frac{6}{2}=-3 \\[ 7pt ] &\quad -\frac{-8}{2}=4 \end{align*}$

また、半径は

$\begin{align*} \quad \frac{\sqrt{64}}{2}=4 \end{align*}$

よって、方程式は

$\begin{align*} &\quad \text{中心} \quad (-3 \ , \ 4 ) \\[ 7pt ] &\quad \text{半径} \quad 4 \end{align*}$

の円を表す。

記述形式では、基本形への変形を示した方が良いでしょう。別解の解法は検算に利用しましょう。

例題(2)の解答・解説

例題(2)

方程式 $x^{2}+y^{2}+2px+3py+13=0$ が円を表すとき、定数 $p$ の値の範囲を求めよ。

例題(2)では、与えられた方程式の係数の一部に文字ｐが含まれています。係数が決まらないので、方程式が円を表すとは言い切れません。

そこで例題(2)では、「方程式が円を表すためのｐの条件を求めよ」という問題になっています。

このような問題であっても、基本形に変形してから考えます。係数に文字ｐが含まれるので、変形ミスに気を付けましょう。

例題(2)の解答例

与式より

$\begin{align*} &\quad x^{2}+y^{2}+2px+3py+13=0 \\[ 7pt ] &\quad \left( x^{2}+2px+p^{2} \right)-p^{2}+\left\{ y^{2}+3py+\left( \frac{3}{2} p \right)^{2} \right\}-\left( \frac{3}{2} p \right)^{2}+13=0 \\[ 7pt ] &\quad \left( x+p \right)^{2}+\left( y+\frac{3}{2} p \right)^{2}=p^{2}+\left( \frac{3}{2} p \right)^{2}-13 \end{align*}$

よって

$\begin{align*} \quad \left( x+p \right)^{2}+\left( y+\frac{3}{2} p \right)^{2}=\frac{13}{4} p^{2}-13 \end{align*}$

この方程式が円をみたすための条件は

$\begin{align*} \quad \frac{13}{4} p^{2}-13 \gt 0 \end{align*}$

これを整理して解くと

$\begin{align*} &\quad p^{2}-4 \gt 0 \\[ 7pt ] &\quad \left(p+2 \right) \left(p-2 \right) \gt 0 \end{align*}$

よって

$\begin{align*} \quad p \lt -2 \ , \ 2 \lt p \end{align*}$

入試レベルの場合、係数に文字が含まれることの方が多いです。ですから、このくらいの変形には充分に慣れておきましょう。

方程式が表す図形は円とは限らない

方程式が表す図形は、例題のように円だけとは限りません。円になるだろうと予想できますが、確認してみないと分かりません。

方程式が表す図形の例１

方程式

$\begin{align*} \quad x^{2}+y^{2}+6x-8y+25=0 \end{align*}$

が表す図形

例題(1)の方程式に似ていますが、定数項が異なります。例題のときと同じように、基本形に変形します。

方程式が表す図形の例１

与式を変形すると

$\begin{align*} &\quad x^{2}+y^{2}+6x-8y+25=0 \\[ 7pt ] &\quad \left( x^{2}+6x+9 \right)-9+\left( y^{2}-8y+16 \right)-16+25=0 \\[ 7pt ] &\quad \left( x+3 \right)^{2}+\left( y-4 \right)^{2}=0 \end{align*}$

右辺が０になってしまいました。文字ｘ，ｙは実数なので、実数の性質を利用して解きます。

方程式が表す図形の例１

$\begin{align*} \quad \left( x+3 \right)^{2}+\left( y-4 \right)^{2}=0 \end{align*}$

これを満たす実数 $x \ , \ y$ は

$\begin{align*} \quad x=-3 \ , \ y=4 \end{align*}$

だけである。

よって、方程式が表す図形は

$\begin{align*} \quad \text{点} \ ( -3 \ , \ 4 ) \end{align*}$

ちなみに、実数の性質は以下の通りです。

実数の性質

$A \ , \ B$ が実数のとき

$\begin{align*} \quad A^{2}+B^{2} \geqq 0 \end{align*}$

また、等号は

$\begin{align*} \quad A=B=0 \end{align*}$

のときに限り成り立つ。

方程式が円ではなく、１点を表す例でした。次を考えてみましょう。

方程式が表す図形の例２

方程式

$\begin{align*} \quad x^{2}+y^{2}+6x-8y+30=0 \end{align*}$

が表す図形

同様にして、基本形に変形します。

方程式が表す図形の例２

与式を変形すると

$\begin{align*} &\quad x^{2}+y^{2}+6x-8y+30=0 \\[ 7pt ] &\quad \left( x^{2}+6x+9 \right)-9+\left( y^{2}-8y+16 \right)-16+30=0 \\[ 7pt ] &\quad \left( x+3 \right)^{2}+\left( y-4 \right)^{2}=-5 \end{align*}$

右辺を見ると、負の数になっています。これを考慮すると以下のようになります。

方程式が表す図形の例２