数学２
今回は、三角形の重心の座標について学習しましょう。三角形の重心は、中点や内分点などと共に頻出です。また、後で学習するベクトルでも頻繁に目にします。
重心の作図の仕方はもちろんですが、その性質や扱い方をしっかりマスターしておきましょう。
数直線上の線分の内分点・外分点
重心のことを学習する前に、内分点と外分点のことを知っておきましょう。
線分を特定の比で分割する点のことを分点と言います。それが線分の内側、つまり線分上にある分点であれば、内分点と言います。
また、線分の外側、つまり線分の延長線上にある分点であれば、外分点と言います。外分点は線分を分割しているとは言い辛いので、初めのうちは理解に苦しむかもしれません。
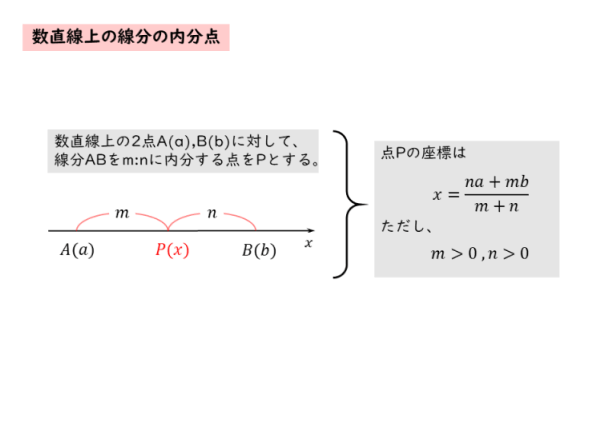
数直線上の線分の内分点
数直線上において、内分点の座標は、以下のように表されます。
数直線上の線分の内分点 1⃣
\begin{align*}
&\text{数直線上の $2$ 点 $A(a),B(b)$ に対して、線分 $AB$ を} \\[ 5pt ]
&\text{$m:n$ に内分する点を $P(x)$ とする。ただし、} \\[ 5pt ]
&\text{$m \gt 0 \ , \ n \gt 0$ とする。} \\[ 5pt ]
&\text{このとき、内分点 $P$ の座標は} \\[ 5pt ]
&\quad x=\frac{na+mb}{m+n}
\end{align*}
内分点の座標を導出してみましょう。
内分点の座標
数直線上の線分の内分点 2⃣
\begin{align*}
&\text{数直線上の $2$ 点 $A(a),B(b)$ に対して、線分 $AB$ を} \\[ 5pt ]
&\text{$m:n$ に内分する点を $P(x)$ とする。ただし、} \\[ 5pt ]
&\text{$m \gt 0 \ , \ n \gt 0$ とする。} \\[ 5pt ]
&\text{このとき} \\[ 5pt ]
&\quad AP:BP=m:n \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad nAP=mBP \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad AP=x-a \ , \ BP=b-x \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad n \left(x-a \right)=m \left(b-x \right) \\[ 7pt ]
&\text{$x$ について整理すると} \\[ 5pt ]
&\quad x=\frac{na+mb}{m+n}
\end{align*}
演習をこなしているうちに覚えていきますが、分母と分子の比の並び（逆になっている）に注目すると覚えやすいかもしれません。
なお、「線分ＡＢを２：１に内分する」と「線分ＢＡを２：１に内分する」は意味が全く異なります。
「線分ＡＢを２：１に内分する」は、点Ａの方から２：１になるように内分するという意味です。それに対して「線分ＢＡを２：１に内分する」は、点Ｂの方から２：１になるように内分するという意味です。
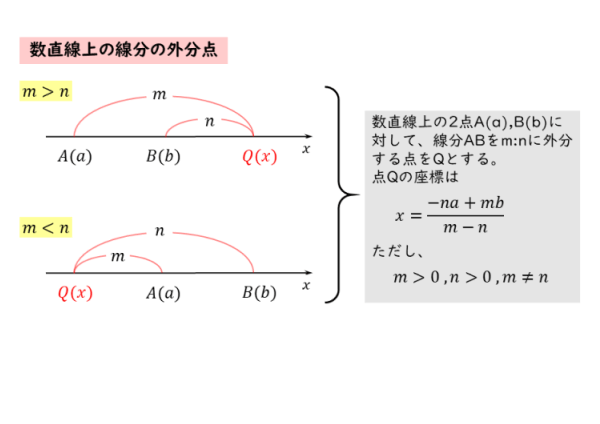
数直線上の線分の外分点
数直線上において、外分点の座標は、以下のように表されます。
数直線上の線分の外分点 1⃣
\begin{align*}
&\text{数直線上の $2$ 点 $A(a),B(b)$ に対して、線分 $AB$ を} \\[ 5pt ]
&\text{$m:n$ に外分する点を $Q(x)$ とする。ただし、} \\[ 5pt ]
&\text{$m \gt 0 \ , \ n \gt 0$ とする。} \\[ 5pt ]
&\text{このとき、外分点 $Q$ の座標は} \\[ 5pt ]
&\quad x=\frac{-na+mb}{m-n} \quad \left(m \neq n \right)
\end{align*}
外分点を扱うとき、内分点よりも注意が必要です。
図から分かるように、外分点の位置は、比のｍとｎの大小によって決まります。比の数字が大きい方が外分点までの距離が長くなり、数字の小さい方が外分点までの距離が短くなります。
どちらも場合であっても、上述した公式で外分点の座標を求めることができますが、外分比に注意しましょう。
線分の外分点の座標 外分点の座標を導出してみましょう。
数直線上の線分の外分点 2⃣
\begin{align*}
&\text{数直線上の $2$ 点 $A(a),B(b)$ に対して、線分 $AB$ を} \\[ 5pt ]
&\text{$m:n$ に外分する点を $Q(x)$ とする。ただし、} \\[ 5pt ]
&\text{$m \gt 0 \ , \ n \gt 0$ とする。} \\[ 5pt ]
&\text{このとき} \\[ 5pt ]
&\quad AQ:BQ=m:n \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad nAQ=mBQ \\[ 7pt ]
&\text{ここで、$m \gt n$ のとき} \\[ 5pt ]
&\quad AQ=x-a \ , \ BQ=x-b \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad n \left(x-a \right)=m \left(x-b \right) \\[ 7pt ]
&\text{$x$ について整理すると} \\[ 5pt ]
&\quad x=\frac{-na+mb}{m-n} \\[ 7pt ]
&\text{これは、$m \lt n$ のときも同様である。}
\end{align*}
内分点の座標を覚えることができれば、外分点の座標を覚えるのは難しくありません。ｎを－ｎに置き換えるだけで済みます。
それよりも、外分点をしっかり作図できるようにしておくことが大切です。意外と作図できないので気を付けましょう。
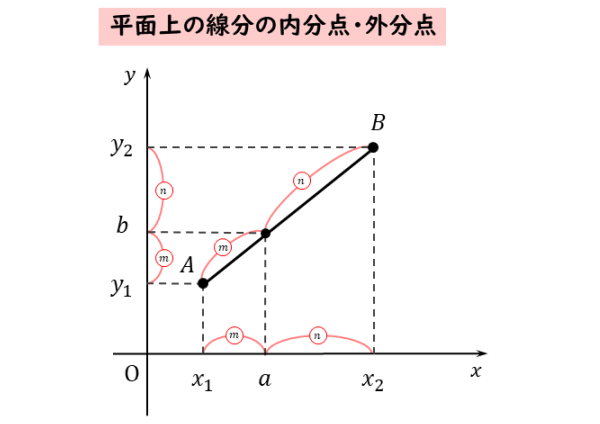
平面上の線分の内分点・外分点
平面上の線分の内分点や外分点を考えます。これらの座標を求めるには、ｘ座標とｙ座標を別々に求めます。
利用するのは、平行線と線分の比の関係です。ｘ軸上だけで見れば、数直線上の線分の内分点や外分点です。ｙ軸上でも同様です。
平行線と線分の関係を利用して軸上で考える 上図では、線分ＡＢの内分点を示していますが、外分点でも考え方は同じです。
平面上の線分の内分点・外分点
\begin{align*}
&\text{$m \gt 0 \ , \ n \gt 0$ のとき、$2$ 点 $A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2})$ に対して、} \\[ 5pt ]
&\text{線分 $AB$ を $m:n$ に内分する点の座標は} \\[ 5pt ]
&\quad \left(\frac{n x_{1}+m x_{2}}{m+n} \ , \ \frac{n y_{1}+m y_{2}}{m+n} \right) \\[ 7pt ]
&\text{また、線分 $AB$ を $m:n$ に外分する点の座標は} \\[ 5pt ]
&\quad \left(\frac{-n x_{1}+m x_{2}}{m-n} \ , \ \frac{-n y_{1}+m y_{2}}{m-n} \right)
\end{align*}
ｘ座標だけ、ｙ座標だけで計算します。２次元で考えるのではなく、１次元に次元を落とすのがコツです。
中点の座標
中点は線分を二等分する点です。見方を変えると、中点は線分を１：１に内分する内分点と考えることができます。ですから、内分点の公式に内分比を代入すると、以下のように表せます。
中点の座標
\begin{align*}
&\text{$A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2})$ とするとき、} \\[ 5pt ]
&\text{線分 $AB$ の中点の座標は} \\[ 5pt ]
&\quad \left(\frac{x_{1}+x_{2}}{2} \ , \ \frac{y_{1}+y_{2}}{2} \right)
\end{align*}
中点の座標を見ると、線分の両端にある２点の座標の平均であることが分かります。
三角形の重心
三角形の重心について、もう一度確認しておきましょう。
三角形の重心は３本の中線の交点です。中線は、頂点とその対辺の中点とを結んだ線分のことです。重心は、中線を２：１に内分する内分点でもあります。
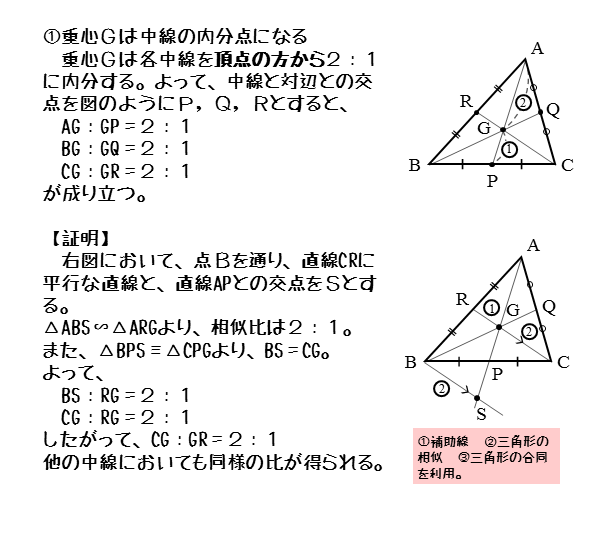重心は中線の内分点 内分比は、中学レベルの知識で導出できるので、きちんとマスターしておきましょう。
三角形の重心の座標
三角形の重心の座標は以下のように表されます。
三角形の重心の座標
\begin{align*}
&\text{$A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2}) \ , \ B(x_{3} \ , \ y_{3})$ とするとき、} \\[ 5pt ]
&\text{$\triangle {ABC}$ の重心の座標は} \\[ 5pt ]
&\quad \left(\frac{x_{1}+x_{2}+x_{3}}{3} \ , \ \frac{y_{1}+y_{2}+y_{3}}{3} \right)
\end{align*}
重心の座標の導出は以下の通りです。
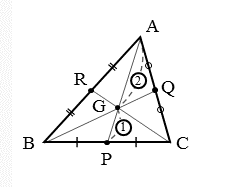三角形の重心の座標
重心の座標の導出
\begin{align*}
&\text{$\triangle {ABC}$ において、辺 $BC$ の中点を $P$、重心を $G$ とする。} \\[ 5pt ]
&\text{また、$A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2}) \ , \ C(x_{3} \ , \ y_{3}) \ , \ G(x \ , \ y)$ とする。} \\[ 5pt ]
&\text{このとき、中点 $P$ の座標は} \\[ 5pt ]
&\quad \left(\frac{x_{2}+x_{3}}{2} \ , \ \frac{y_{2}+y_{3}}{2} \right) \\[ 7pt ]
&\text{また、重心 $G$ は線分 $AP$ を $AG:GP=2:1$ に内分するので} \\[ 5pt ]
&\text{$x$ 座標について} \\[ 5pt ]
&\quad x=\frac{ \left(1 \cdot x_{1}+2 \cdot \frac{x_{2}+x_{3}}{2} \right)}{2+1} \\[ 7pt ]
&\text{が成り立つ。} \\[ 5pt ]
&\text{これを整理すると} \\[ 5pt ]
&\quad x=\frac{x_{1}+x_{2}+x_{3}}{3} \\[ 7pt ]
&\text{$y$ 座標も同様にして} \\[ 5pt ]
&\quad y= \frac{y_{1}+y_{2}+y_{3}}{3} \\[ 7pt ]
&\text{したがって、重心 $G$ の座標は} \\[ 5pt ]
&\quad \left(\frac{x_{1}+x_{2}+x_{3}}{3} \ , \ \frac{y_{1}+y_{2}+y_{3}}{3} \right)
\end{align*}
重心の座標を見ると、三角形の３頂点の座標の平均であることが分かります。
点の座標を求めてみよう
内分点や外分点などの点の座標を求めてみましょう。
例題
\begin{align*}
&(1) \quad \text{座標平面上に $3$ 点 $A(3 \ , \ 4) \ , \ B(-3 \ , \ 1) \ , \ C(5 \ , \ -2)$ がある。} \\[ 5pt ]
&\qquad \text{このとき、線分 $AB$ を $2:1$ に内分する点 $D$ の座標を求めよ。} \\[ 5pt ]
&\qquad \text{また、線分 $AC$ を $3:1$ に外分する点 $E$ の座標を求めよ。} \\[ 10pt ]
&(2) \quad \text{$3$ 点 $(-1 \ , \ 2) \ , \ (3 \ , \ -4) \ , \ (7 \ , \ -4)$ を頂点とする} \\[ 5pt ]
&\qquad \text{三角形の重心の座標を求めよ。}
\end{align*}
例題(1)の解答・解説
例題(1)
\begin{align*}
&\text{座標平面上に $3$ 点 $A(3 \ , \ 4) \ , \ B(-3 \ , \ 1) \ , \ C(5 \ , \ -2)$ がある。} \\[ 5pt ]
&\text{このとき、線分 $AB$ を $2:1$ に内分する点 $D$ の座標を求めよ。} \\[ 5pt ]
&\text{また、線分 $AC$ を $3:1$ に外分する点 $E$ の座標を求めよ。}
\end{align*}
比に注意しましょう。線分ＡＢをＡの方から２：１に内分します。点Ｄは、ＡＤ：ＢＤ＝２：１となる位置にあります。
はじめに、内分点Ｄの座標を求めます。公式を覚えるために、対応する値を代入しただけの式を記述しましょう。整理するのはそのあとで構いません。
例題(1)の解答例 1⃣
\begin{align*}
&\text{内分点 $D$ の座標は} \\[ 5pt ]
&\quad \left(\frac{1 \cdot 3+2 \cdot (-3)}{2+1} \ , \ \frac{1 \cdot 4+2 \cdot 1}{2+1} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad D \ (-1 \ , \ 2)
\end{align*}
次に、外分点Ｅの座標を求めます。比に注意しましょう。線分ＡＣをＡの方から３：１に外分します。点Ｅは、ＡＥ：ＣＥ＝３：１となる位置にあります。外分点なので、点Ｃ側を延長しなければなりません。
例題(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad D \ (-1 \ , \ 2) \\[ 7pt ]
&\text{外分点 $E$ の座標は} \\[ 5pt ]
&\quad \left(\frac{(-1) \cdot 3+3 \cdot 5}{3-1} \ , \ \frac{(-1) \cdot 4+3 \cdot (-2)}{3-1} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad E \ (6 \ , \ -5)
\end{align*}
例題(2)の解答・解説
例題(2)
\begin{align*}
&\text{$3$ 点 $(-1 \ , \ 2) \ , \ (3 \ , \ -4) \ , \ (7 \ , \ -4)$ を頂点とする} \\[ 5pt ]
&\text{三角形の重心の座標を求めよ。}
\end{align*}
公式に代入して三角形の重心の座標を求めます。
例題(2)の解答例
\begin{align*}
&\text{重心の座標は} \\[ 5pt ]
&\quad \left(\frac{(-1)+3+7}{3} \ , \ \frac{2+(-4)+(-4)}{3} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad (3 \ , \ -2)
\end{align*}
重心の座標は、分母が３と決まっているので、内分点や外分点に比べると覚えやすいでしょう。
次は、三角形の重心の座標を扱った問題を実際に解いてみましょう。
