図形の性質|重心について

今回は重心について学習しましょう。重心は五心の1つです。五心には外心や内心も含まれます。
この重心を扱った問題は、図形を扱う単元(たとえばベクトル)では頻出です。重心のもつ性質やそれに関わる公式などを使いこなせるようにしておきましょう。
なお、記事の画像が見辛いときはクリックすると拡大できます。
重心について
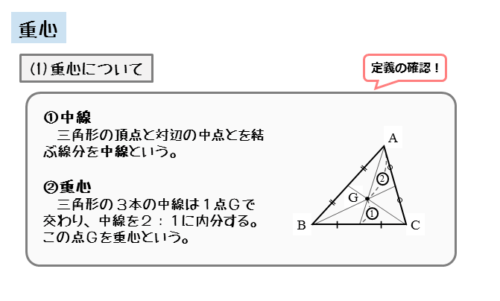
三角形の頂点と対辺の中点とを結んだ線分のことを中線と言います。
三角形では中線を3本引けますが、この3本の中線は1点で交わります。この交わってできた点が重心です。一般に、重心のことをアルファベットでGと表します。
重心の作図の仕方を覚えておきましょう。頂点とその対辺の中点を結びます。この線分が中線です。
中線を3本引くと、中線が1点で交わるはずです。この点が重心になります。重心は、中線を2本引いた時点でできるので、簡単に済ませたければ、中線を2本引くだけで良いでしょう。
重心には大切な性質があります。それは、重心が中線を頂点側から2:1に内分する性質をもつということです。
重心は三角形の3中線の交点。また、重心は中線を頂点側から2:1に内分する内分点。
重心の性質
重心の性質についてはすでに触れましたが、重心は主に2つの性質をもちます。重心を扱った問題では、どちらかの性質に絡んだ問題が出題されることがほとんどです。
重心の性質
- 中線を頂点側から2:1に内分する
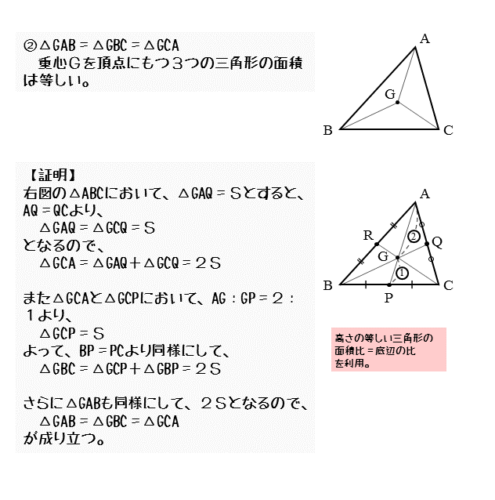
- 重心Gを頂点にもつ3つの三角形の面積は等しい
それぞれの性質がなぜ成り立つのかを知っておくと理解が深まります。性質の導出では、これまでに学習した知識を利用するからです。良い復習になるので積極的に取り組みましょう。
重心による内分比の導出
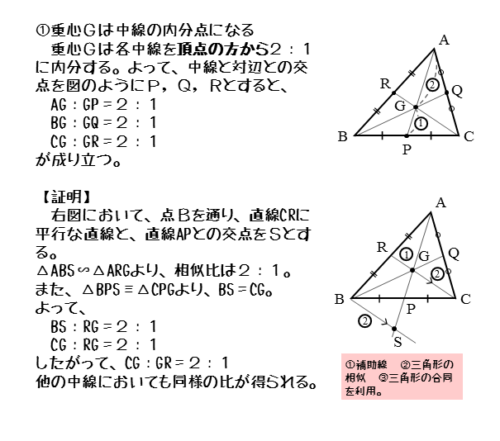
△ABCにおいて、辺BC,CA,ABの中点をそれぞれP,Q,Rとします。また、3本の中線AP,BQ,CRの交点である重心をGとします。
このとき、各中線AP,BQ,CRは重心Gによって頂点の方から2:1に内分されます。
この性質を導出してみましょう。補助線が必要なので、初見で証明するのは難しいと思います。一度は自分で作図しながら導出しておきましょう。
図のような△ABCにおいて、3本の中線AP,BQ,CRを引くと、重心Gができます。
まず、補助線を引きます。
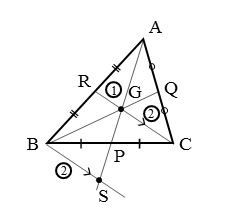
たとえば、頂点Bを通り、中線CRに平行な直線を引きます。この補助線と直線APとの交点をSとします。
次に、△ABSと△ARGに注目します。2本の直線CR,BSが平行であることから、△ABSと△ARGは相似な三角形となります。2組の角がそれぞれ等しいという相似条件が成り立ちます。
△ABSと△ARGの関係
$\triangle ABS$ と $\triangle ARG$ において
共通角より
\begin{align*} \quad \angle {BAS} = \angle {RAG} \end{align*}$CR \parallel BS$ より、同位角が等しいので
\begin{align*} \quad \angle {ABS} = \angle {ARG} \end{align*}$2$ 組の角がそれぞれ等しくなるので
\begin{align*} \quad \triangle {ABS} \ \text{∽} \ \triangle {ARG} \end{align*}△ABSと△ARGの相似比は、AR=RBであるので2:1です。また、相似な三角形において、対応する辺の比は相似比に等しいので、BS:RG=2:1です。
次に、△BPSと△CPGに注目します。
こちらも2本の直線CR,BSが平行であることから、△BPSと△CPGは合同な三角形となります。1組の辺とその両端の角がそれぞれ等しいという合同条件が成り立ちます。
△BPSと△CPGの関係
$\triangle BPS$ と $\triangle CPG$ において
\begin{align*} \quad BP = CP \end{align*}対頂角より
\begin{align*} \quad \angle {BPS} = \angle {CPG} \end{align*}$CR \parallel BS$ より、錯角が等しいので
\begin{align*} \quad \angle {PBS} = \angle {PCG} \end{align*}$1$ 組の辺とその両端の角がそれぞれ等しくなるので
\begin{align*} \quad \triangle {BPS} \ \equiv \ \triangle {CPG} \end{align*}△BPSと△CPGが合同な三角形となるので、BS=CGが成り立ちます。これとBS:RG=2:1を用いると、BS:RG=CG:RG=2:1を導くことができます。
これで重心Gによる中線CRの内分比を導出できました。他の中線についても同じようにして、重心Gによる内分比を導出することができます。
「重心は中線を頂点の方から2:1に内分する」ことの証明についてまとめると以下のようになります。
数学1・Aで学習する内容は、そのほとんどが中学の発展内容のようなものです。ですから、中学で学習した内容を上手に利用することで公式や定理を導出することできます。
公式や定理などの導出は、既習内容を使いこなすための良い訓練になります。面倒臭がらずに積極的に取り組みましょう。理解が深まるだけでなく、応用力もしっかりと身に付きます。
重心Gを頂点にもつ三角形の関係
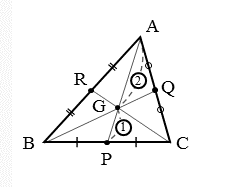
△ABCにおいて、重心をGとします。このとき、△GBC,△GCA,△GABは重心Gを頂点にもつ三角形です。
このような重心Gを頂点にもつ三角形の面積は等しくなります。
この性質を導出してみましょう。図のような△ABCにおいて、△GAQ=Sとします。
まず、△GAQと△GCQに注目します。
底辺をそれぞれAQ,QCとすると、△GAQと△GCQの高さは、頂点Gから下した垂線の長さで共通となります。
高さが等しいとき、三角形の面積比は底辺の比に等しくなる性質があります。
この関係を参考にして、△GACをSを用いて表します。
△GACの面積をSを用いて表す
$\triangle {GAQ}$ と $\triangle {GCQ}$ の面積比は
\begin{align*} \quad \triangle {GAQ} : \triangle {GCQ} = AQ : QC \end{align*}ここで、$AQ : QC = 1:1$ より
\begin{align*} \quad \triangle {GAQ} : \triangle {GCQ} = 1 : 1 \end{align*}よって
\begin{align*} \quad \triangle {GAQ} = \triangle {GCQ} \end{align*}このとき
\begin{align*} \quad \triangle {GAQ} = \triangle {GCQ} = S \end{align*}とすると
\begin{align*} \quad \triangle {GCA} = 2S \end{align*}2つの三角形の高さが等しいとき、(面積比)=(底辺比)が成り立つ。
次に、△GCAと△GCPの関係や、△GCPと△GBPの関係に注目します。ここでも(面積比)=(底辺の比)が成り立つことを利用します。
△GBCの面積をSを用いて表す
$\triangle {GCA}$ と $\triangle {GCP}$ の面積比は
\begin{align*} \quad \triangle {GCA} : \triangle {GCP} = AG : GP \end{align*}$AG : GP = 2:1$ より
\begin{align*} \quad \triangle {GCA} : \triangle {GCP} = 2 : 1 \end{align*}$\triangle {GCA} = 2S$ より
\begin{align*} \quad \triangle {GCP} = S \end{align*}また、$CP : BP = 1:1$ より
\begin{align*} \quad \triangle {GCP} : \triangle {GBP} = 1:1 \end{align*}$\triangle {GCP} = \triangle {GBP} = S$ より
\begin{align*} \quad \triangle {GBC} = 2S \end{align*}△GABについても同じようにして考えると、△GAB=2Sと表せます。以上のことから、重心を頂点にもつ3つの三角形の面積は等しくなります。
「重心を頂点にもつ3つの三角形の面積は等しい」ことの証明についてまとめると以下のようになります。
次は、重心を扱った問題を実際に解いてみましょう。