図形の性質｜外心について

11/13/2021数学Ａ

今回は外心について学習しましょう。外心は図形を扱った問題では頻出です。外心のもつ性質やそれに関わる公式などを使いこなせるようにしておきましょう。

記事の画像が見辛いときはクリックすると拡大できます。

外心について

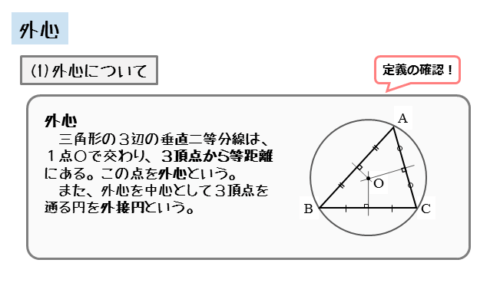
外心とは、三角形に外接する円の中心のことです。また、三角形に外接する円のことを外接円と言います。

円が三角形に外接するとき、三角形の３つの頂点は外接円の周上にあります。

外心の作図の仕方を覚えておきましょう。

三角形の３辺の垂直二等分線を描くと、交点ができます。この交点が外心になります。また、交点を中心にして、三角形の頂点を通るように円を描くと、三角形の外接円を描くことができます。

外心を作図してみるとその性質が分かってきます。

３辺の垂直二等分線を引いたので、外心は三角形の頂点から等しい距離にあります。ですから、外心と頂点の距離は、外接円の半径に等しくなります。

外心は３辺の垂直二等分線の交点。また、外心と頂点の距離は、外接円の半径に等しい。

外心や外接円と関わりのある事柄は主に３つあります。外心や外接円を扱った問題のパターンと考えても良いかもしれません。

外心や外接円と関わりのある事柄

中心角と円周角の関係は、外接円に限ったことではなく円全般に言えますが、三角形や四角形の内角と関連付けた問題がよく出題されます。

中心角や円周角を扱うときに気を付けたいことは、中心角や円周角が同一の弧（弦）に対してできた角かどうかです。

中心角や円周角と弧の関係は、扇形をイメージすると判断しやすいのではないかと思います。自分なりの判別方法を見つけておくと良いでしょう。

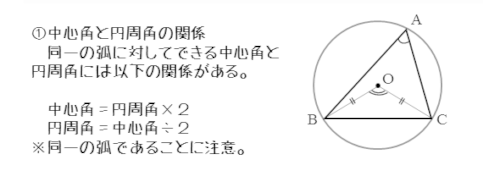
同一の弧に対してできた中心角と円周角の間には以下のような関係があります。

同一の弧に対してできた中心角と円周角の関係

\begin{align*} \quad \text{(中心角)} &= \text{(円周角)} \times 2 \\[ 10pt ] \text{(円周角)} &= \text{(中心角)} \times \frac{1}{2} \end{align*}

厳密に言えば「等しい長さの弧に対して」であって、必ずしも同一の弧である必要はありません。

しかし、そこまで捻った問題はほとんど出題されないので、まずは同一の弧に対してできた中心角と円周角を探しましょう。

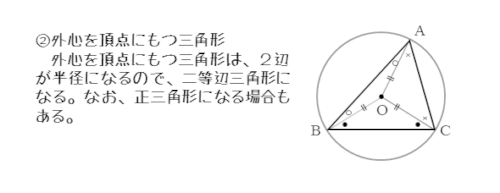
三角形の頂点の１つが外心であるとき、２辺の長さは外接円の半径に等しくなります。

図のように、Ｏを中心とする円が△ＡＢＣに外接するとします。

このとき、ＯＡ，ＯＢ，ＯＣの長さは半径に等しいので、△ＯＡＢ，△ＯＢＣ，△ＯＣＡは二等辺三角形です。場合によっては正三角形になることもあります。

二等辺三角形であれば、底角が等しくなります。また、∠ＡＯＢ，∠ＢＯＣ，∠ＡＯＣは、三角形の内角の１つですが、中心角でもあります。他の内角は、円周角の一部になっています。

二等辺三角形の内角が中心角や円周角と関わるので、角の大きさを求める問題がよく出題されます。

円を扱った問題で角の大きさを問われたとき、半径を上手に使って二等辺三角形や正三角形を作ることが取っ掛かりの１つになります。

三角形の外接円では、外心と頂点を結んで、３つの二等辺三角形（または正三角形）を作ろう。

これまでをまとめると以下のようになります。

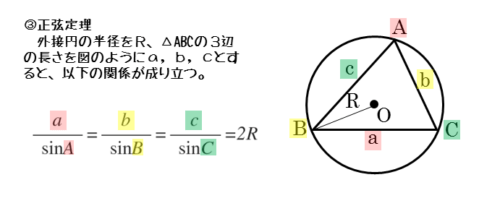
正弦定理については、図形の計量の単元で学習済みです。外接円が出てくると、正弦定理を扱った問題がほぼ確実に出題されます。

この単元では角度を求めることが主題になっているので、正弦定理の出番はほとんどありません。

しかし、この単元は正弦定理を始め、三角形の面積や面積比などと関連するので、関連性を意識しながら演習をこなしておきましょう。

次は実際に問題を解いてみましょう。

Posted by kiri