確率|事象と確率について

今回から「確率」の単元を学習します。
確率を扱った問題を解けるようになるには、場合の数に関する知識が必要です。場合の数を数え上げられないと、残念ながらほとんどの問題で確率を求めるところまで到達できません。
場合の数で学習したことを確認しながら、確率の学習に取り組むと良いでしょう。
事象と確率について
確率は中学でも学習する単元ですが、覚えるべき公式は大したことはありません。
もちろん、中学とは異なり、より専門的な内容になるので、新しい用語や定義が紹介されています。その点では理解するのに苦労するかもしれません。
そうは言っても、確率を扱った問題を解けるかどうかは、場合の数をきちんと数え上げられるかどうかで決まると言っても言い過ぎではないと思います。
場合の数を正確に数え上げることができれば、ほとんどの問題で確率を求めることができるはずです。
そのためにも場合の数を扱った問題を一通り解けるようにしておくことが最低限の準備になります。
試行と事象、確率
試行と事象
単元の導入部分では、決まって新しい用語や定義についての紹介です。ここでしっかり理解して覚えてしまうことが大切です。
確率の単元を通してよく用いられるのが、「試行」や「事象」などの用語です。
試行
ある特定の条件で繰り返すことができ、偶然によって結果が決まる実験などのこと。
言い換えると、試行は、「くじを1本引く」や「1つのサイコロを投げる」など、あるルールに従って行う操作と捉えても良いでしょう。
事象
試行の結果起こる事柄のこと。また、1つの試行において、起こりうる結果のそれぞれを根元事象、その全体を全事象と言う。
1つの試行を行ったとき、起こりうる結果のそれぞれを要素と言うことがあります。つまり、事象はいくつかの要素をもつ部分集合と考えると分かりやすいです。
そのように考えると、全事象はすべての事象を含む全体集合と捉えることができます。なお、全事象は全体集合と同じように一般にUと表します。
確率
さいごに確率です。中学のときよりも少し細かいですが、確率を考えるときに大事な条件があります。
それは「すべての根元事象が同じ程度に起こると期待できるとき」という条件です。これを一般に「どの根元事象も同様に確からしいとき」と言います。
この条件が成り立つとき、事象Aが起こる確率をP(A)という記号で表します。また、その確率P(A)は以下の式で表されます。
事象Aが起こる確率P(A)
どの根元事象も同様に確からしいとする。
このときの事象 $A$ が起こる確率 $P(A)$ は
\begin{align*} \quad P(A) = \frac{ \text{事象 $A$ が起こる場合の数} }{ \text{起こりうるすべての場合の数} } \end{align*}事象Aが起こる場合の数は、事象Aの要素の数n(A)です。また、起こりうるすべての場合の数は、全事象Uの要素の数n(U)です。
これらから、確率P(A)はさらに以下のように表せます。
事象Aが起こる確率P(A)
どの根元事象も同様に確からしいとする。
このときの事象 $A$ が起こる確率 $P(A)$ は
\begin{align*} \quad P(A) &= \frac{ \text{事象 $A$ が起こる場合の数} }{ \text{起こりうるすべての場合の数} } \\[ 10pt ] &= \frac{n(A)}{n(U)} \end{align*}上述の式から、確率を求めるためには、場合の数を正しく数え上げることが必要であることが分かります。「場合の数」を制することが確率を制することだと言っても過言ではないでしょう。
これまでをまとめると以下のようになります。
試行と事象の関係
用語の定義は文言通り覚える必要がありますが、理解するのは具体例の方が良いでしょう。
試行は、たとえば「サイコロを1回投げる」「3枚のカードから無作為に1枚を引く」「3人でじゃんけんをする」などに相当します。
これらは人為的な操作がない限り、その結果が偶然によって決まるので試行になります。
色々な試行がありますが、「サイコロを1回投げる」という試行を考えてみましょう。
この試行において、1の目が出る、2の目が出る・・・という結果、つまり事象が起こります。
試行 … サイコロを1回投げる
サイコロを1回投げることによって起こる事象
- 1の目が出る
- 2の目が出る
- 3の目が出る
- 4の目が出る
- 5の目が出る
- 6の目が出る
この試行では「1の目の出る」という結果は1通りだけなので、「1の目の出る」という結果は1つだけの要素をもつ事象です。ですから、この事象は根元事象と言えます。他の目についても同じです。
そして、これらの根元事象をまとめた全体が全事象となります。全事象は6つの(根元)事象をまとめた全体となるので、その要素の数は6つです。
先ほど述べたように、全事象が全体集合、根元事象が要素を1つだけもつ部分集合、全事象も根元事象も広義の意味で集合と捉えると分かりやすいのではないかと思います。
「同様に確からしい」とは
先ほど確率の説明で「同様に確からしい」という文言が出てきました。
この文言は問題文にも出てきますが、問題を解くための解法を知っていれば、文言の意味を知らなくても支障が出ることはないかもしれません。そのせいか、あまり意識しなくなります。
しかし、意味も分からず問題を解いているよりも、きちんと意味を理解しておいた方が良いに決まっています。せっかくなので「同様に確からしい」の意味を例を使って考えてみましょう。
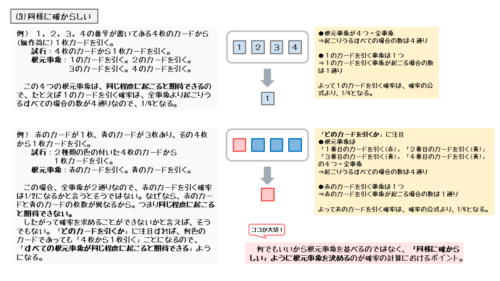
この試行における事象を整理してみましょう。4枚のカードから1枚を引く試行を行ったとき、それで起こる事象は以下のようになります。
試行 … 1~4の番号が振られた4枚のカードから1枚を引く
1~4の番号が振られた4枚のカードから1枚を引くことによって起こる事象
- 1のカードを引く
- 2のカードを引く
- 3のカードを引く
- 4のカードを引く
数字の出方はそれぞれ1通りずつなので、各事象の要素は1つだけになります。ですから、各事象はどれも根元事象と言えます。
また、全事象は4つの根元事象全体となり、その要素は4つです。
これら4つの根元事象は、人為的な操作がない限り、同じ程度に起こると期待できます。つまり「同様に確からしい」事象です。
このとき、1のカードを引く確率は4分の1になります。もちろんその他のカードを引く確率もそれぞれ4分の1です。
次は数字ではなく、色が塗られたカードを考えてみましょう。
色に注目して事象を考えてみると以下のようになります。
試行 … 1枚を赤、残り3枚を青に塗られた4枚のカードから1枚を引く
1枚を赤、残り3枚を青に塗られた4枚のカードから1枚を引くことによって起こる事象
- 赤色のカードを引く
- 青色のカードを引く
この事象をもとに赤色のカードを引く確率を考えてみましょう。
色は赤と青の2種類なので、赤色のカードを引く確率は2分の1になりそうですが、果たしてそうでしょうか?
赤色のカードを引く確率が2分の1ではないことは明らかですが、意外とやってしまう間違いです。なぜこのような間違いが起こったのでしょうか。
2分の1の確率ということは、起こりうるすべての場合の数が、赤色と青色の2通りしかないと考えたからかもしれません。
この考え方だと、赤色のカードを引く事象と青色のカードを引く事象とが、要素を1つだけもつ根元事象だと考えたことになります。
色に注目した場合、事象は「赤色のカードを引く事象」と「青色のカードを引く事象」の2つです。これは正しいのですが、それぞれの事象に注目してみると、2つの事象の違いに気付きます。
赤色のカードは1枚だけなので、その引き方は1通りです。ですから、赤色のカードを引く事象は要素を1つだけもつ根元事象と言えます。
しかし、青色のカードは3枚あるので、その引き方は3通りあります。各カードの引き方であれば1通りずつですが、色で事象を考えたので、1通りではありません。
このことから、青色のカードを引く事象は、3つの根元事象を要素にもつので、根元事象とは言えません。
青色のカードを引く事象
- 青色のカードその1を引く
- 青色のカードその2を引く
- 青色のカードその3を引く
赤色のカードを引く事象は根元事象であるのに対して、青色のカードを引く事象は根元事象ではありません。
要素の数を比べても分かるように、明らかに青色の方に偏りが出ます。このように、色に対して根元事象を定めると、同じ程度に起こると期待できないので、「同様に確からしい」とは言えません。
起こりうる結果のことを事象と言うので、何に注目するかで事象の捉え方は変わります。それは構わないのですが、その事象が根元事象かどうかを考える必要があります。
例から分かるように、根元事象が何かを見誤ると、確率を正しく求めることができません。
確率の値は、事象の数ではなく、根元事象の数によって定まります。どの事象が同じ程度に起こるのかを把握することは、場合の数を求めるためにもとても大切なことです。
どの結果が根元事象なのかをしっかり把握しよう。
偏りのない状態が「同様に確からしい」状態
色つきカードの例を番号つきカードの例と同じように扱うには、「どのカードを引くか」に注目します。
「どのカードを引くか」に注目するということは、たとえ同じ色であっても、4枚のカードのそれぞれを別物と区別するということです。
このように「どのカードを引くか」に注目すれば、どのカードも4枚のうちの1枚になります。その結果、カードの引かれ方は1通りずつになり、同じ程度に期待できます。
もちろん、各事象は要素を1つだけもつ根元事象になります。すべての根元事象は、同じ程度に起こると期待できる状態です。
このように「同じ程度に起こると期待できる」根元事象をもとに、他の事象を考えることが大切です。これができるようになると、場合の数を正しく数え上げることができ、確率の値も正しく求めることができます。
確率の問題を解くときに注意すべきは、同じ程度に起こると期待できる根元事象を決めること。
これまでをまとめると以下のようになります。
次は、確率を扱った問題を実際に解いてみましょう。