確率|反復試行の確率について

今回は反復試行の確率について学習しましょう。独立な試行の確率と同じように重要な単元です。入試でも頻出なので、しっかりマスターしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
反復試行とその確率
反復試行とは、ある試行を独立に何度も繰り返して行う試行のことです。
たとえば「1枚の硬貨を3回投げる」や「1個のサイコロを3回投げる」などの試行は、硬貨やサイコロを投げるという試行を繰り返し行っています。それに加えて、繰り返し行われる試行は、結果が互いに影響を与えません。ですから、これらの試行は反復試行です。
このような反復試行の確率の求め方をマスターしましょう。
反復試行の確率を求めよう
反復試行の確率の定義
反復試行の確率を求めるには、独立な試行の確率に関する知識を必要とします。不安な人は、独立な試行の確率の単元を確認しながら学習すると良いでしょう。
一般に、1回の試行で事象Aが起こる確率をpとして、この試行をn回繰り返し行うとき、事象Aがちょうどk回起こる確率は、以下の式で表されます。
反復試行の確率
$1$ 回の試行で事象 $A$ が起こる確率を $p$ として、この試行を $n$ 回繰り返し行うとき、事象 $A$ がちょうど $k$ 回起こる確率は
\begin{align*} \quad {}_n \mathrm{ C }_k \cdot p^{k} \cdot \left( 1-p \right)^{n-k} \end{align*}式中の(1-p)は、事象Aの余事象が起こる回数です。事象Aがn回のうちk回だけ起こるので、事象A以外の事象、つまり事象Aの余事象が(n-k)回だけ起こります。忘れないように注意しましょう。
これまでをまとめると以下のようになります。
反復試行の確率を導出しよう
反復試行の確率は上述のように定義されますが、どのようにして導出されるのかを考えてみましょう。導出までの過程を知ることで、より理解が深まるはずです。
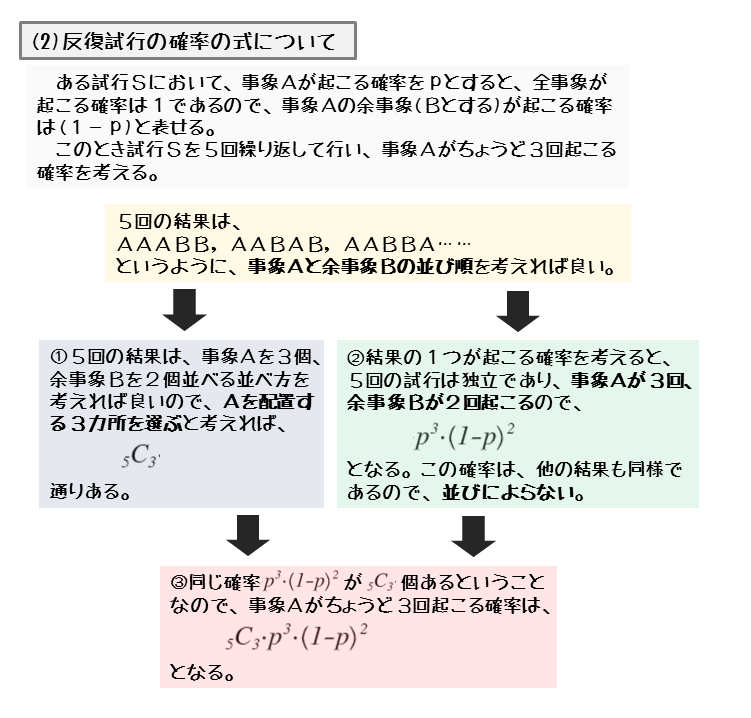
たとえば、ある試行Sにおいて、事象Aが起こる確率をpとします。試行Sを5回行ったとき、事象Aがちょうど3回起こる確率を求めてみましょう。
5回の試行Sの結果の総数
5回の試行Sのうち、事象Aは3回起こりますが、残り2回では事象Aは起こりません。残り2回では、A以外の事象が起こります。
事象A以外の事象とは、事象Aの余事象(Bとする)のことです。この余事象Bが起こる確率は、全事象が起こる確率1と事象Aが起こる確率pから、(1-p)と表されます。
5回の試行Sの内訳
- 事象A … 3回、確率p
- 事象Aの余事象B … 5-3=2回、確率(1-p)
また、試行Sを5回行ったときの結果は「AAABB」「AABBA」などいくつか考えられます。これらは事象Aと余事象Bの並べ方を考えることで数え上げることができます。
並べ方を考えるので、3個のAと2個のBを一列に並べる順列を考えれば良いことが分かります。ただし、同じものを含む順列になるので、このようなときには組合せの考え方を利用します。
3個のAと2個のBを一列に並べる順列の総数は、5カ所からAを配置する3カ所を選ぶときの組合せの総数に等しくなります。このとき、組合せの総数は全部で5C3通りあります。
3個のAと2個のBを一列に並べる順列の総数
$3$ 個の $A$ と $2$ 個の $B$ を一列に並べる順列の総数は、$5$ カ所から $A$ を配置する $3$ カ所を選ぶ組合せの総数に等しいので
\begin{align*} \quad {}_5 \mathrm{ C }_3 = \frac{5!}{3! \cdot 2!} \end{align*}もちろん順列の総数でも求めることができますが、定義では組合せの方が採用されています。
結果の確率を求めよう
結果の総数を求めたので、次は結果の1つに注目します。結果の1つである「AAABB」の確率を求めてみましょう。1~5回の試行は互いの結果に影響を与えないので独立な試行です。
ですから「AAABB」が起こる確率は、事象Aが起こる確率pと余事象Bが起こる確率(1-p)の積で表されます。
「AAABB」が起こる確率
「$AAABB$」が起こる確率は、事象 $A$ が起こる確率 $p$ と余事象 $B$ が起こる確率 $(1-p)$ の積で表されるので
\begin{align*} \quad p \cdot p \cdot p \cdot \left( 1-p \right) \cdot \left( 1-p \right) = p^{3} \cdot \left( 1-p \right)^{2} \end{align*}5C3通りある結果から1つだけ取り出して確率を求めました。他の結果も考えてみると、事象A,Bが起こる回数は同じです。ですから、掛ける順番は異なりますが、確率は同じ式で表されます。
このことから分かるのは、同じ積で表される式が5C3個あるということです。
事象Aがちょうど3回起こる確率を求めよう
同じ確率となる結果が全部で5C3個あることが分かりました。このことから、事象Aがちょうど3回起こる確率は以下のように表されます。
事象Aがちょうど3回起こる確率
事象 $A$ が $3$ 回起こり、事象 $B$ が $2$ 回起こる場合の数は、全部で ${}_5 \mathrm{ C }_3$ 通りあるので、事象 $A$ がちょうど $3$ 回起こる確率は
\begin{align*} \quad p^{3} \cdot \left(1-p \right)^{2} \times {}_5 \mathrm{ C }_3 = {}_5 \mathrm{ C }_3 \cdot p^{3} \cdot \left(1-p \right)^{2} \end{align*}このようにして反復試行の確率は導出されます。具体例を使って考えると、組合せや余事象の話が出てくることも分かると思います。
これを一般化したものが先ほどの反復試行の確率の式になります。ただの暗記で済まさず、導出の課程を理解することが大切です。
これまでをまとめると以下のようになります。
次は反復試行を扱った問題を実際に解いてみましょう。