図形と方程式|円の方程式の基本形と一般形について

今回は、円の方程式の基本形と一般形について学習しましょう。
これまで図形と方程式を学習してきましたが、直線から円に変わります。円を中心に学習しますが、直線もそのうち関わってきます。
円を綺麗に図示するのは意外と難しいです。日頃から書き慣れておくことが大切です。
円の方程式
円の方程式の基本形
円の方程式は、円という図形の性質から導かれます。円は、ある1点からの距離がつねに一定となる点の集まりです。このある1点が円の中心です。
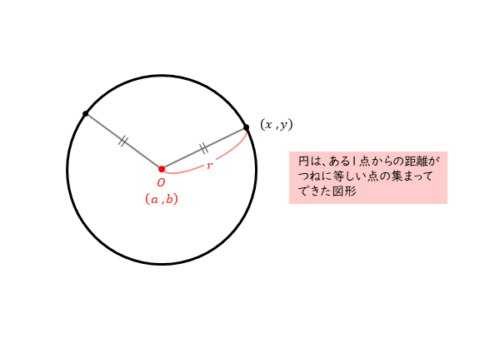
このことを知っていれば、自分で導くことができるので、円の方程式をわざわざ暗記する必要はないでしょう。実際に、円の方程式を導いてみましょう。
円の方程式を導く
点 $O(a \ , \ b)$ と任意の点 $(x \ , \ y)$ との間の距離を $r$ とすると
\begin{align*} \quad \sqrt{\left(x-a \right)^{2}+\left(y-b \right)^{2}}=r \end{align*}よって、円の方程式は
\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}これを円の方程式の基本形と言う。
ある1点(中心)と、任意の点(円周上の点)との間の距離がつねに一定となることを利用して、2点間の距離の式で導きます。
両辺を2乗すると、円の方程式になります。また、導かれた方程式のことを、一般に円の方程式の基本形と言います。
円の方程式(基本形)
中心が $(a \ , \ b)$ で、半径が $r$ の円の方程式
\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}特に、中心が原点の場合、円の方程式は以下の通りです。
円の中心が原点の場合
円の方程式
\begin{align*} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align*}において
\begin{align*} \quad a=0 \ , \ b=0 \end{align*}であるから
\begin{align*} \quad x^{2}+y^{2}=r^{2} \end{align*}ある点の座標を原点の座標に置き換えるだけです。
円の方程式の一般形
円の方程式の基本形を展開した形もあります。これを円の方程式の一般形と言います。
円の方程式(一般形)
円の方程式の一般形は
\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}残念ながら、いつも基本形が与えられるとは限りません。問題では、一般形の方が多いかもしれません。
そんな一般形ですが、イマイチなところは、円の方程式だと分かっても、中心の座標や半径を知ることはできないことです。
円を扱う上で大切な情報は、中心の座標と半径です。この2つの情報があれば、円を図示できます。
一般形で与えられていれば、迷うことなく基本形に変形します。基本形への変形では、平方完成を利用します。
一般形から基本形への変形
円の方程式を
\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \end{align*}とする。
$x \ , \ y$ について平方完成すると
\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\frac{l^{2}}{4}+\left(y+\frac{m}{2} \right)^{2}-\frac{m^{2}}{4}+n=0 \end{align*}整理すると
\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\left(y+\frac{m}{2} \right)^{2}=\frac{l^{2}+m^{2}-4n}{4} \end{align*}一般形から基本形に変形することができました。この式の右辺から色々と分かることがあります。
一般形から基本形に変形して分かること
\begin{align*} \quad \left(x+\frac{l}{2} \right)^{2}+\left(y+\frac{m}{2} \right)^{2}=\frac{l^{2}+m^{2}-4n}{4} \end{align*}① $l^{2}+m^{2}-4n \gt 0$ のとき
\begin{align*} \quad \text{中心} \ \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \ , \ \text{半径} \ \frac{\sqrt{l^{2}+m^{2}-4n}}{2} \end{align*}② $l^{2}+m^{2}-4n = 0$ のとき
\begin{align*} \quad \text{円は点} \ \left(-\frac{l}{2} \ , \ -\frac{m}{2} \right) \ \text{を表す} \end{align*}③ $l^{2}+m^{2}-4n \lt 0$ のとき
\begin{align*} \quad \text{表す図形はない} \end{align*}基本形において、右辺は半径を2乗したものです。右辺の平方根をとったとき、分子には根号が付きます。この根号の中にある式の値によって、円ができるかどうかを判別できます。
根号の中にある式の値が、円の成立条件に関わるので覚えておきましょう。
一般形から基本形への変形で分かったことをまとめると、以下の通りです。
一般形で表される円の方程式の特徴
- x,yの2次方程式
- x2とy2の係数が等しい
- xyの項がない
- ℓ2+m2-4n>0(半径>0)
2番目と3番目は意外と盲点で、これが成り立たないと、基本形に変形できません。
円の方程式を求めてみよう
円の方程式を求めてみましょう。
例題
$(1) \ 2$ 点 $(3 \ , \ 4) \ , \ (5 \ , \ -2)$ を直径の両端とする円の方程式を求めよ。
$(2) \ 3$ 点 $(3 \ , \ 1) \ , \ (6 \ , \ -8) \ , \ (-2 \ , \ -4)$ を通る円の方程式を求めよ。
基本形と一般形の使い分けができるようになりましょう。
例題(1)の解答・解説
例題(1)
$2$ 点 $(3 \ , \ 4) \ , \ (5 \ , \ -2)$ を直径の両端とする円の方程式を求めよ。
作図すると、以下の通りです。
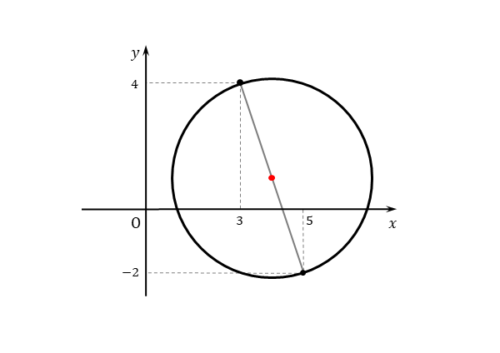
例題(1)では、直径の両端となる2点の座標が与えられています。この2点を結ぶ線分が直径となるので、直径の中点が円の中心です。
例題(1)の解答例 1⃣
$2$ 点 $(3 \ , \ 4) \ , \ (5 \ , \ -2)$ を結ぶ線分の中点の座標は
\begin{align*} \quad \left(\frac{3+5}{2} \ , \ \frac{4-2}{2} \right) \end{align*}よって
\begin{align*} \quad (4 \ , \ 1 ) \end{align*}これが円の中心となる。
円の中心の座標が分かりました。この中心と直径の端点との距離が半径となります。
両端の点の座標が与えられているので、計算しやすい方を選びましょう。また、半径を求めるために、直径を求めて2で割っても良いでしょう。
例題(1)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}$2$ 点 $(3 \ , \ 4) \ , \ (4 \ , \ 1)$ 間の距離が半径 $r$ となるので
\begin{align*} \quad r^{2}=\left(4-3 \right)^{2}+\left(1-4 \right)^{2} \end{align*}よって
\begin{align*} \quad \quad r^{2}=10 \end{align*}中心の座標と半径(の2乗)が分かったので、基本形に代入します。
例題(1)の解答例 3⃣
\begin{align*} \quad \vdots \end{align*}よって、中心 $(4 \ , \ 1)$ で、半径の $2$ 乗が $10$ となる円の方程式は
\begin{align*} \quad \left(x-4 \right)^{2}+\left(y-1 \right)^{2}=10 \end{align*}円の中心、または半径が与えられた場合、円の方程式は基本形で。
例題(2)の解答・解説
例題(2)
$3$ 点 $(3 \ , \ 1) \ , \ (6 \ , \ -8) \ , \ (-2 \ , \ -4)$ を通る円の方程式を求めよ。
例題(2)では、円周上にある3点の座標が与えられています。
しかし、これでは円の中心の座標を求めることはできません。このような場合に、一般形を利用します。
例題(2)の解答例 1⃣
求める円の方程式を
\begin{align*} \quad x^{2}+y^{2}+lx+my+n=0 \quad \cdots \text{①} \end{align*}とする。
円の方程式を定めたら、この式と与えられた3点の座標を用います。
円周上にある点の座標を方程式に代入すると等式を満たすことを利用します。
例題(2)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x^{2}+y^{2}+lx+my+n=0 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \end{align*}円が点 $(3 \ , \ 1)$ を通るので、①に代入すると
\begin{align*} \quad 3^{2}+1^{2}+l \cdot 3+m \cdot 1+n=0 \end{align*}よって
\begin{align*} \quad 3l+m+n+10=0 \quad \cdots \text{②} \end{align*}円が点 $(6 \ , \ -8)$ を通るので、①に代入すると
\begin{align*} \quad 6^{2}+\left(-8 \right)^{2}+l \cdot 6+m \cdot \left(-8 \right)+n=0 \end{align*}よって
\begin{align*} \quad 6l-8m+n+100=0 \quad \cdots \text{③} \end{align*}円が点 $(-2 \ , \ -4)$ を通るので、①に代入すると
\begin{align*} \quad \left(-2 \right)^{2}+\left(-4 \right)^{2}+l \cdot \left(-2 \right)+m \cdot \left(-4 \right)+n=0 \end{align*}よって
\begin{align*} \quad 2l+4m-n-20=0 \quad \cdots \text{④} \end{align*}3つの方程式を導くことができました。未知の数に対して、同じ数だけ方程式が必要です。
これらを連立して解きます。
例題(2)の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 3l+m+n+10=0 \quad \cdots \text{②} \\[ 7pt ] &\quad 6l-8m+n+100=0 \quad \cdots \text{③} \\[ 7pt ] &\quad 2l+4m-n-20=0 \quad \cdots \text{④} \end{align*}③-②より
\begin{align*} \quad 3l-9m+90=0 \end{align*}整理すると
\begin{align*} \quad l-3m+30=0 \quad \cdots \text{⑤} \end{align*}③+④より
\begin{align*} \quad 8l-4m+80=0 \end{align*}整理すると
\begin{align*} \quad 2l-m+20=0 \quad \cdots \text{⑥} \end{align*}⑤-⑥×3より
\begin{align*} \quad -5l-30=0 \end{align*}よって
\begin{align*} \quad l=-6 \end{align*}これと⑤より
\begin{align*} \quad -6-3m+30=0 \end{align*}よって
\begin{align*} \quad m=8 \end{align*}$l=-6 \ , \ m=8$ を②に代入して
\begin{align*} \quad 3 \cdot \left(-6 \right)+8+n+10=0 \end{align*}よって
\begin{align*} \quad n=0 \end{align*}したがって、求める円の方程式は
\begin{align*} \quad x^{2}+y^{2}-6x+8y=0 \end{align*}円周上にある3点の座標が与えられた場合、一般形を利用するのが定石です。
ただし、少し面倒な連立方程式を解かなければなりません。例題(2)のように、3つの方程式を連立して解く場合、計算ミスに気を付けましょう。
円が通る3点の座標が与えられた場合、円の方程式は一般形で。計算ミスに注意。
次は、円の方程式の基本形と一般形を扱った問題を実際に解いてみましょう。











