図形と方程式｜座標を利用した証明（垂心）について
今回は、座標を利用した証明について学習しましょう。座標を利用した証明についてはすでに学習していますが、ここでは垂線を扱う垂心に関わる証明です。
座標を用いることで証明しやすくなるのですが、上手に座標平面に図形を設置できなければ、かえって難しくなります。そうならないように、ポイントをしっかり押さえましょう。
座標を利用した証明（垂心）
垂心は五心の１つです。ただ、内心・外心・重心に比べると、垂心を扱った問題はあまり見かけません。
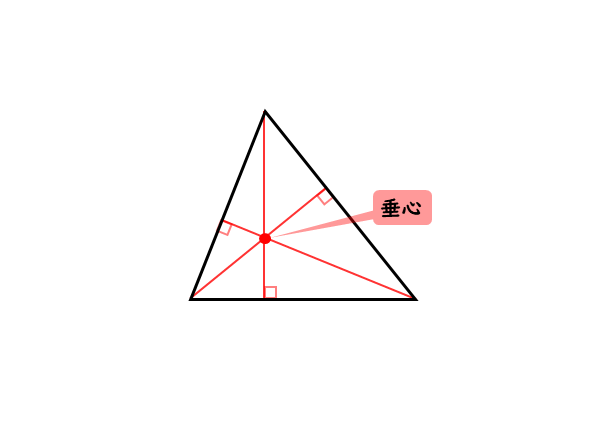
垂心は、三角形の３つの頂点から対辺にそれぞれ下した垂線の交点です。
証明問題としては、３つの頂点からそれぞれ下した垂線が１点で交わることを証明する問題が出題されます。この証明を図形的にやろうと思えば、かなり難しく、そして面倒です。
このような証明あっても、座標平面上に三角形を設置することで簡単に証明できるようになります。
座標を利用した証明はすでに学習していますが、ここでは、座標軸が予め定められています。座標軸を自分で設定する問題よりも取り組みやすいでしょう。
座標を利用して証明してみよう（垂心）
例題
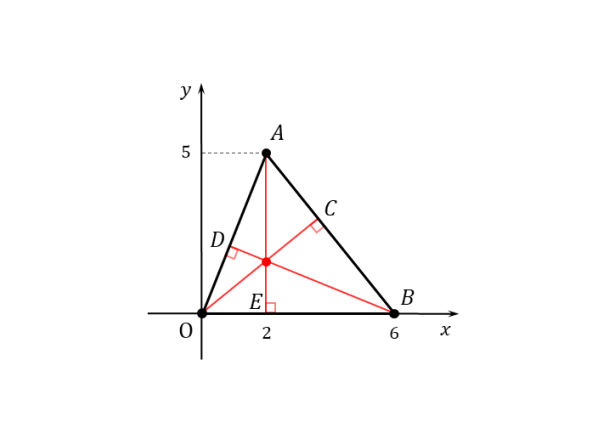
座標平面上の $3$ 点 $O(0 \ , \ 0) \ , \ A(2 \ , \ 5) \ , \ B(6 \ , \ 0)$ を頂点とする $\triangle {OAB}$ の各頂点から対辺に下した垂線は $1$ 点で交わることを証明せよ。
例題の解答・解説
例題では、三角形の頂点の座標が予め与えられているので、座標軸は自分で設定する必要はありません。問題文に合わせて作図しましょう。
３直線が１点で交わることを証明するには、２直線の交点が残りの直線上にあることを示すことが一般的です。
例題では、作図すると分かりますが、頂点Ａから下した垂線がｘ軸に垂直です。このことを利用すると一般的な証明よりも簡単になります。
まず、直線ＡＢの傾きから垂線ＯＣの方程式を求めます。
例題の解答例 1⃣
直線 $AB$ の傾きは
\begin{align*} \quad \frac{0-5}{6-2}=-\frac{5}{4} \end{align*}頂点 $O$ から対辺 $AB$ に下した垂線 $BD$ の傾きは
\begin{align*} \quad \frac{4}{5} \end{align*}よって、頂点 $O$ から対辺 $AB$ に下した垂線 $OC$ の方程式は
\begin{align*} \quad y=\frac{4}{5} x \quad \cdots \text{①} \end{align*}垂線ＯＣは原点を通る直線なので、切片はありません。
また、傾きを求めるために、２直線の垂直条件を利用しています。
２直線の垂直条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}同じ要領で、直線ＯＡの傾きから垂線ＢＤの方程式を求めます。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=\frac{4}{5} x \quad \cdots \text{①} \end{align*}また、直線 $OA$ の傾きは $\frac{5}{2}$ より、頂点 $B$ から対辺 $OA$ に下した垂線 $BD$ の傾きは
\begin{align*} \quad -\frac{2}{5} \end{align*}よって、垂線 $BD$ の方程式は
\begin{align*} \quad y-0=-\frac{2}{5} \left(x-6 \right) \end{align*}すなわち
\begin{align*} \quad y=-\frac{2}{5} x+\frac{12}{5} \quad \cdots \text{②} \end{align*}垂線ＢＤの方程式を求めるために、１点の座標（点Ｂ）と傾きを利用しています。
直線の方程式
[１] 点 $(x_{1} \ , \ y_{1})$ を通り、傾きを $m$ とする直線の方程式は
\begin{align*} \quad y-y_{1}=m \left( x-x_{1} \right) \end{align*}[２] 点 $(x_{1} \ , \ y_{1})$ を通り、$x$ 軸に垂直な直線の方程式は
\begin{align*} \quad x=x_{1} \end{align*}これで、２つの垂線ＯＣ，ＢＤの方程式が分かりました。
これらの方程式を連立すれば、交点の座標を求めることができます。これが一般的な解法です。
ここでは、垂線ＡＥがｘ軸に垂直な直線であることを利用します。
垂線ＯＣと垂線ＡＥの交点の座標と、垂線ＢＤと垂線ＡＥの交点の座標とを比べます。こちらの方が、垂線ＯＣと垂線ＢＤの交点の座標を求めるよりもはるかに簡単です。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=\frac{4}{5} x \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad y=-\frac{2}{5} x+\frac{12}{5} \quad \cdots \text{②} \end{align*}頂点 $A$ から対辺 $OB$ に下した垂線 $AE$ の方程式は
\begin{align*} \quad x=2 \quad \cdots \text{③} \end{align*}①に $x=2$ を代入すると
\begin{align*} \quad y=\frac{4}{5} \cdot 2=\frac{8}{5} \end{align*}②に $x=2$ を代入すると
\begin{align*} \quad y=-\frac{2}{5} \cdot 2+\frac{12}{5}=\frac{8}{5} \end{align*}よって、$3$ 直線①，②，③は $1$ 点
\begin{align*} \quad \left(2 \ , \ \frac{8}{5} \right) \end{align*}で交わる。
したがって、$\triangle {OAB}$ の各頂点から対辺に下した $3$ つの垂線は $1$ 点で交わる
２つの垂線ＯＣ，ＡＥの交点のｙ座標を求めるには、垂線ＯＣの方程式にｘ＝２を代入します。同様に、２つの垂線ＢＤ，ＡＥの交点のｙ座標を求めるには、垂線ＢＤの方程式にｘ＝２を代入します。
この２つのｙ座標が一致すれば、交点が一致すると言えます。
それに対して、２つの垂線ＯＣ，ＢＤの交点の座標を求めるには、２つの垂線ＯＣ，ＢＤの方程式を連立して解く必要があります。どちらが楽な計算かは明らかです。
また、垂線が出てくるのは、垂心に限ったことではありません。外心の証明でも出てきます。慣れておきましょう。
次は、座標を利用した証明（垂心）を扱った問題を実際に解いてみましょう。