図形の性質|作図について

今回は作図について学習しましょう。
高校の数学では、試験でも基本的にフリーハンドで作図することが多くなります。それに伴って、定規やコンパスを使う機会がほとんどありません。
どちらかと言うと、中学生に知っておいてほしい内容です。ただ、作図では図形の性質を上手に利用するので、高校生にとっても十分に参考になると思います。
記事の画像が見辛いときはクリックすると拡大できます。
定規とコンパスの決まった使い方
作図とは、定規とコンパスだけを使って、次の2つの規約に基づき、与えられた条件を満たす図形を書くことです。定規の目盛りや三角定規の角などは使えないので注意しましょう。
作図の規約(作図の公法)
- 定規:与えられた2点を通る直線を引く。線分を延長する。
- コンパス:与えられた1点を中心として、与えられた半径をかく。線分の長さを移す。
2つの規約は作図の公法とも言われます。このような規約を守って作図するわけですが、特に作図できるようにしておきたい図形は4つあります。
作図できるようにしておきたい図形
- 垂直二等分線
- (特定の)点を通る垂線
- 角の二等分線
- (特定の)点を通る平行線
その他にも「線分を移す」「角を移す」「線分の分点」などの作図もあり、上記の4つと併せて7つの作図を基本作図と言います。
線分の垂直二等分線を引こう
垂直二等分線とは、線分を二等分するだけでなく、その線分に対して垂直な直線のことです。
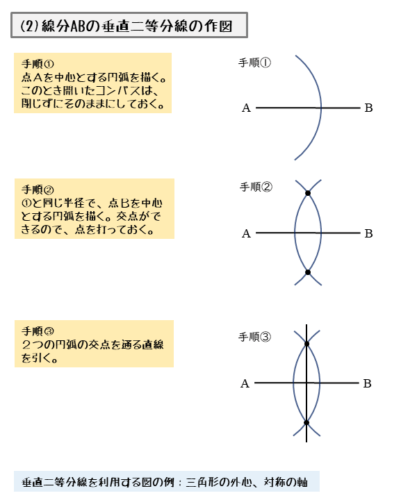
線分ABの垂直二等分線を引いてみましょう。手順は3つあります。
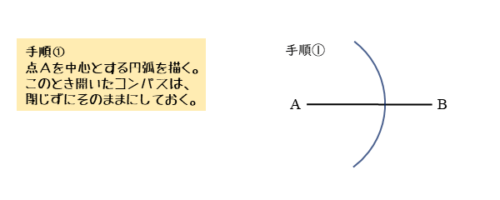
垂直二等分線の手順①
コンパスを使って、点Aを中心とする円(弧)を描きます。
コンパスの開き具合いは、線分ABの半分よりも大きくなるようにしましょう。また、この後も同じ半径の円(弧)を描くので、コンパスを閉じずに開いたままにしておきます。
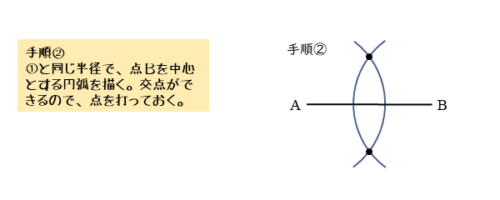
垂直二等分線の手順②
手順①と同じ要領でコンパスを使って、今度は点Bを中心とする円(弧)を描きます。
コンパスを開いたままにしておいたので、手順①のときと同じ半径の円(弧)を描くことができます。
点Aを中心とする円(弧)と、点Bを中心とする円(弧)が交わって、線分ABの上下に交点が2つできます。交点だと分かるように、点を打っておくと良いでしょう。
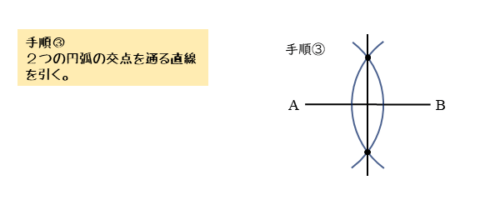
垂直二等分線の手順③
2つの交点を通る直線を定規を使って引きます。これが線分ABの垂直二等分線です。
このような手順で線分ABの垂直二等分線を作図することができます。
垂直二等分線かどうかを調べてみよう
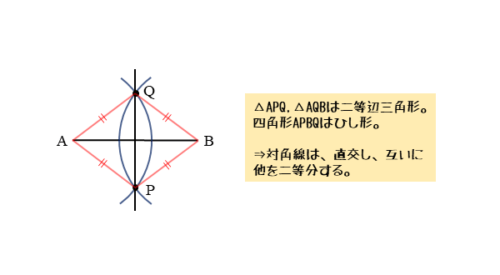
作図した直線が垂直二等分線であることを確かめるには、△APB,△AQBや四角形APBQを見ると分かります。
AP=BP=AQ=BQとなるように作図したので、△APBと△AQBは合同な二等辺三角形になります。また、四角形APBQはひし形になります。
ひし形は4辺が等しい平行四辺形と考えるとイメージしやすいでしょう。このひし形は、2本の対角線が直交し、かつ互いに他を二等分するという性質をもちます。
AB,PQはひし形の対角線になっているので、PQはABの垂直二等分線になります。また、垂直二等分線の作図では、ひし形を作ろうとしていることも分かります。
線分の垂直二等分線は、ひし形の対角線を作図している。
垂直二等分線の性質
垂直二等分線のもつ性質として、垂直二等分線上の点から2点A,Bまでの距離は等しい(AP=BP,AQ=BQ)という性質があります。
この性質が成り立つのは、2点P,Qが垂直二等分線上のどこにあっても、△APBと△AQBが合同な二等辺三角形になるからです。
このような線分ABの垂直二等分線は、2つの定点A,Bから等距離にある点の集まり(軌跡)になります。
垂直二等分線を作図するような状況として、たとえば、外心や線対称の軸を作図するときに利用されます。このことは「軌跡」の単元でも出題されるので覚えておきましょう。
垂直二等分線は、外心や線対称の軸を作図する問題で出題される。
線分ABの垂直二等分線を引く手順の一覧です。
特定の点を通る垂線を引こう
垂線とは、ある直線に対して垂直な直線のことです。もちろん、線分ABの垂直二等分線も垂線です。
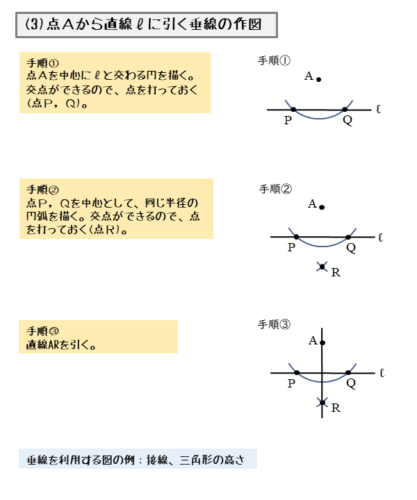
直線ℓに対して、点Aを通る垂線を引いてみましょう。ただし、点Aは直線ℓ上にない点です。手順は3つあります。
垂線の手順①
コンパスを使って、点Aを中心とする、直線ℓと交わる円(弧)を描きます。コンパスを開いたままにしておきます。
直線ℓとの交点が2つできます。2つの交点をP,Qとすると、AP=AQです。
垂線の手順②
手順①と同じ要領でコンパスを使って、今度は点P,Qをそれぞれ中心とする円(弧)を描きます。このとき、直線ℓに関して点Aと反対側に円(弧)を描きます。
2つの円(弧)が交わって交点ができます。この交点をRとすると、同じ半径の円(弧)を描いたので AP=AQ=PR=QRです。これで4辺が等しい四角形(ひし形)ができていることが分かります。
垂線の手順③
2点A,Rを通る直線を定規で引きます。この直線ARが点Aを通る垂線です。
点Aを通る直線ARが、直線ℓに対して垂直であることは、2つの直線AR,ℓがひし形である四角形APRQの対角線であることから明らかです。このような垂線は、たとえば、接線や三角形の高さを作図するときに利用されます。
垂線は、接線や三角形の高さを作図する問題で出題される。
点Aを通る垂線を引く手順の一覧です。
次は、角の二等分線や点を通る平行線の作図です。