図形の性質｜多面体について

11/16/2018数学Ａ多面体,オイラーの多面体定理,正多面体

今回は多面体について学習しましょう。

この単元も直接的に出題されることが少ない単元です。この単元からの出題であれば、知識だけで解ける問題がほとんどではないかと思います。ただ、実際は面積や体積などに派生した問題に発展するので、知らなくて良いわけではありません。

なお、記事の画像が見辛いときはクリックすると拡大できます。

参考
図形の性質｜円周角について
図形の性質｜円に内接する四角形について
図形の性質｜接線と弦について
図形の性質｜方べきの定理について
図形の性質｜2円の位置関係について
図形の性質｜作図について
公式・定理集｜図形の性質
数学1・A｜2017センター試験・第5問を解いてみよう

多面体

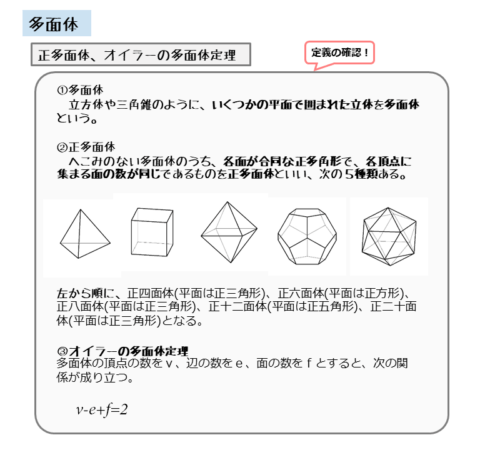
多面体とは、立方体や三角錐のように、いくつかの平面で囲まれた立体のことです。この単元では、主に正多面体とオイラーの多面体定理について学習します。

正多面体の定義

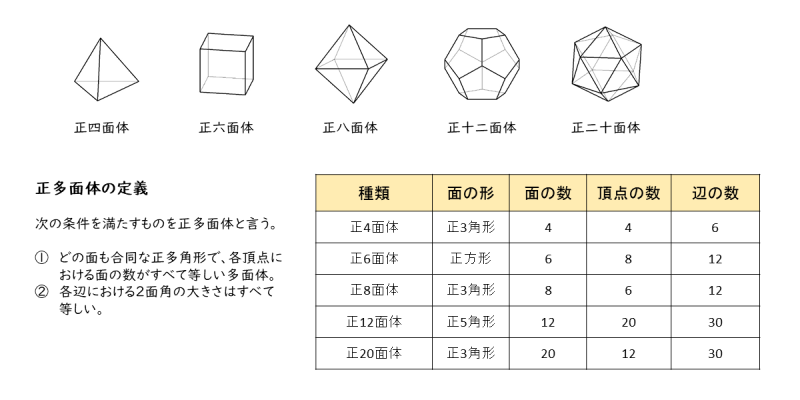
へこみのない多面体(凸多面体と言う)のうち、各面が合同な正多角形で、各頂点に集まる面の数が同じであるものを正多面体と言います。

正多面体の定義
へこみのない多面体において、以下の条件を満たす立体のこと。

すべての面が合同な正多角形である
すべての頂点に集まる面の数が同じある

正多面体の種類

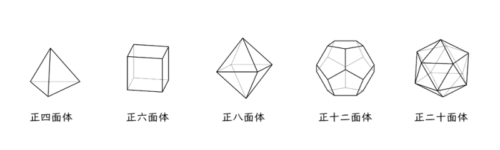
正多面体には、正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類あります。

正六面体は立方体の方が分かりやすいかもしれません。また、正四面体から正八面体までは、空間図形の問題でも扱うので、馴染みのある立体かもしれません。

このような正多面体では、面の形や面の数などがすでに分かっています。

種類	面の形	面の数	頂点の数	辺の数
正4面体	正3角形	4	4	6
正6面体	正方形	6	8	12
正8面体	正3角形	8	6	12
正12面体	正5角形	12	20	30
正20面体	正3角形	20	12	30

似たような数字が出てくるので間違えないようにしましょう。セットにして覚えるのは、正六面体と正八面体、正十二面体と正二十面体です。

正多面体についての一覧は以下のようになります。

オイラーの多面体定理

多面体の頂点、辺、面の数について以下の関係が成り立ちます。

オイラーの多面体定理
\begin{align*}
&\quad \bigl( \text{頂点の数} \bigr) \ – \bigl( \text{辺の数} \bigr) + \bigl( \text{面の数} \bigr) = 2 \\[ 5pt ]
&\text{または} \\[ 5pt ]
&\quad \bigl( \text{頂点の数} \bigr) + \bigl( \text{面の数} \bigr) = \bigl( \text{辺の数} \bigr) + 2
\end{align*}

このような関係、または関係式をオイラーの多面体定理と言います。オイラーの多面体定理は、オイラーの多面体公式とも言われます。確認してみると分かりますが、どの正多面体でもオイラーの多面体定理が成り立っています。

あとでオイラーの多面体定理を扱った問題を解いてみますが、この式を使うだけなのですぐに慣れると思います。

これまでのまとめです。