図形の性質|多面体について

多面体を扱った問題を解いてみよう
次の問題を解いてみましょう。
問(1)の解答・解説
問(1)
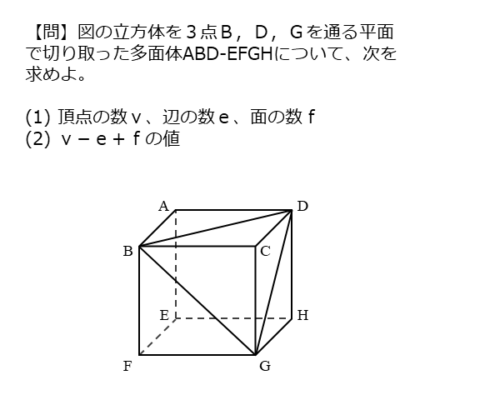
立方体 $ABCD-EFGH$ を $3$ 点 $B , \ D , \ G$ を通る平面で切り取った多面体 $ABD-EFGH$ について、頂点の数 $v$、辺の数 $e$、面の数 $f$ を求めよ。
問(1)は、与えられた多面体の頂点、辺、面の数をそれぞれ求める問題です。与えられた多面体は、立方体から三角錐を取り除かれた形をしています。
立体の名称(表し方)には規則があります。規則を守って名称を記述しましょう。
角柱のように底面2つのものは、底面-底面のように表す。また、角錐のように頂点1つ、底面1つのものは、頂点-底面のように表す。多面体ABD-EFGHは、面ABDと面EFGHを底面とする立体を表す。
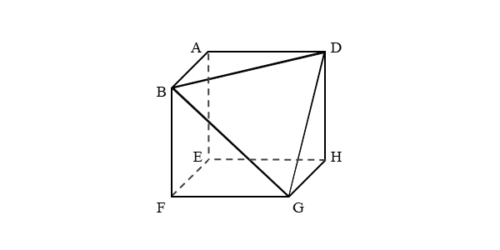
三角錐が取り除かれるので、三角錐が残ったままだと数え間違う可能性があります。ケアレスミスを減らすために、多面体ABD-EFGHを自分で作図しましょう。
三角錐を取り除く前と比べてみると、全く違って見えるはずです。
自分で作図した多面体を見ながら数えていきます。数えるときのコツは、上から下へ、または右から左へなど、自分なりにルールを決めて数えたり、数えた頂点や辺に印をつけたりすることです。
問(1)の解答例
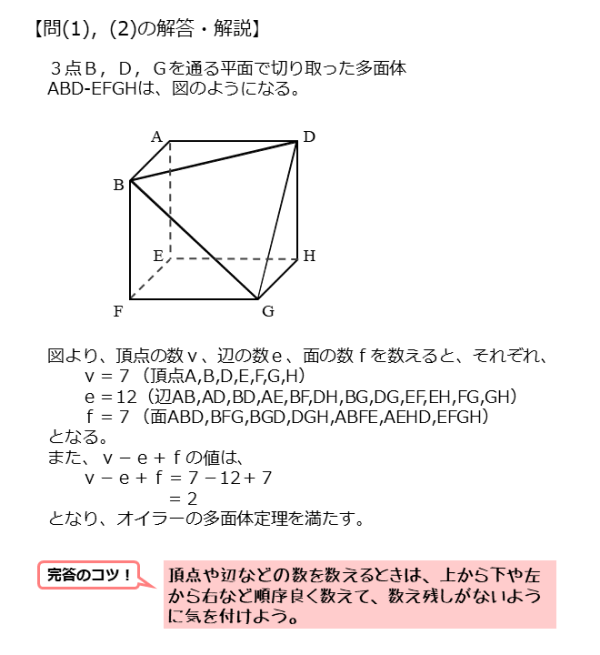
多面体 $ABD-EFGH$ の上側から下側へ順に数えていく。
頂点の数 $v$ : $v=7$
辺の数 $e$ : $e=12$
面の数 $f$ : $f=7$
問(2)の解答・解説
問(2)
立方体 $ABCD-EFGH$ を $3$ 点 $B , \ D , \ G$ を通る平面で切り取った多面体 $ABD-EFGH$ について、$v – e + f$ の値を求めよ。
問(2)は、オイラーの多面体定理を扱った問題です。オイラーの多面体定理を知っていれば、計算せずに答えを出すことができます。
オイラーの多面体定理
\begin{align*} \quad \text{(頂点の数)}-\text{(辺の数)}+\text{(面の数)} = 2 \end{align*}または
\begin{align*} \quad \text{(頂点の数)} + \text{(面の数)} = \text{(辺の数)} + 2 \end{align*}問(1)で求めた頂点、辺、面の数を与式に代入して計算します。
問(2)の解答例
$(1)$ より
\begin{align*} \quad v – e + f &= 7-12+7 \\[ 7pt ] &=2 \end{align*}オイラーの多面体定理の式を満たしていることが分かります。
問のポイントと解答例をまとめると以下のようになります。
立体を分割した問題になると、自分で作図した方が良い場合が多いです。基本的には込み入った計算がなく、辺や面の数を正しく数え上げれば良いので、それほど難易度は高くありません。
Recommended books
どんな人でも、現物をじかに見たり、触ったりしたことがある方が、イメージがより具体的になります。見たり、触ったりしたことのないものでは、イメージに限界があります。
空間図形を苦手にしている人は意外と多いですが、それは実物を見たり、触ったりした経験がないことが原因かもしれません。
オススメする書籍には、色々な多面体が紹介されています。もちろん、実際に作成できるので、実物を見たり、触ったりすることができます。立体図形に関する感覚(空間把握力)が以前よりも向上するかもしれません。興味のある方はぜひ一読を。
オススメその1
おすすめしたい書籍の1つ目は、『ストローとモールでつくる幾何学オブジェ 100均グッズで学ぶ多面体』です。
本書では、入手しやすいストローやモールを材料にして多面体を作成します。その作品数は30種類以上です。慣れてきたら、折り紙で多面体作成に挑戦しても良いかもしれません。
オススメその2
おすすめしたい書籍の2つ目は、『はじめての多面体おりがみ新装版 考える頭をつくろう!』です。
多面体をつくると言えば、折り紙を使うことを思いつきますが、初心者には敷居が高く感じてしまいます。しかし、本書は初心者向けの入門書なので、取り組みやすいかと思います。
折り紙チャンピオン(テレビ東京)で準優勝となった著者が、幾何学的な折り紙を楽しく、易しく紹介してくれます。タイルやレンガ、直角コーナー、角柱、角錐、正多面体、星形、風車まで様々な多面体を作成できます。
さいごに、もう一度、頭の中を整理しよう
- 正多面体は5種類。
- 正多面体について、面の形や面の数などを覚えておこう。
- 立体を分割してできた多面体の扱いには注意しよう。
- オイラーの多面体定理を知っておくと、頂点、辺、面の数の検算ができる。