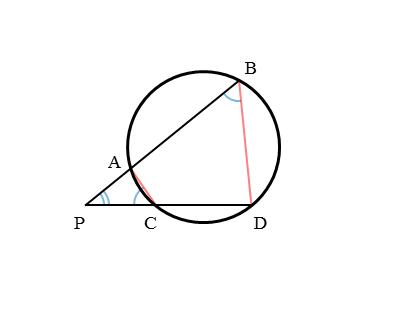図形の性質|方べきの定理について

今回は方べきの定理について学習しましょう。
接弦定理と同じく頻出の単元です。三角形と併せて出題されることが多いのが特徴です。三角形とセットで出題される理由は、方べきの定理の成り立ちを知ると納得できるでしょう。
接弦定理と同じように、図形とセットで定理を覚え、図形を見たときに瞬時に判断できるようにしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
方べきの定理とその逆
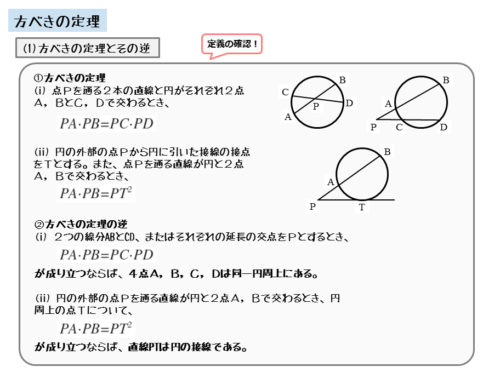
方べきの定理
方べきの定理が成り立つためには、いずれかの条件を満たす必要があります。
方べきの定理が成り立つための条件
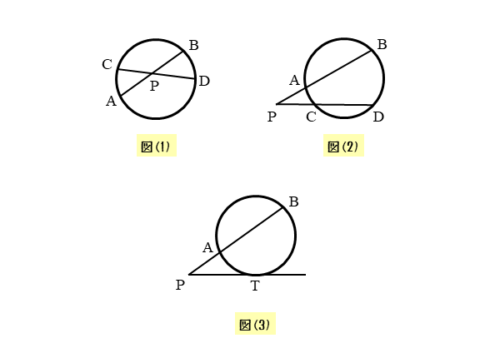
- 円の内部または外部で交点をもつ2本の直線が、円とそれぞれ2点で交わる。(図(1),(2))
- 円の外部で交点をもつ2本の直線のうち、1本が円と2点で交わり、もう1本が円と接する。(図(3))
1つ目の条件を満たすとき、各線分PA,PB,PC,PDの関係を以下のような式で表せます。
方べきの定理 1⃣
\begin{align*} \quad PA \cdot PB = PC \cdot PD \quad \cdots \text{①} \ \text{(図(1),(2))} \end{align*}2つ目の条件を満たすとき、各線分PA,PB,PTの関係を以下のような式で表せます。
方べきの定理 2⃣
\begin{align*} \quad PA \cdot PB = {PT}^2 \quad \cdots \text{②} \ \text{(図(3))} \end{align*}上述した条件を満たすとき、各線分の長さの関係を式で表せること、またはその式のことを方べきの定理と言います。
方べきの定理の逆
方べきの定理の逆が成り立つには、いずれかの条件を満たす必要があります。
方べきの定理の逆が成り立つための条件
- 2つの線分AB,CD、またはそれぞれの延長の交点をPとするとき、①式が成り立つ。
- 円の外部の点Pを通る直線が円と2点A,Bで交わるとき、円周上の点Tについて、②式が成り立つ。
1つ目の条件を満たすとき、4点A,B,C,Dは同一円周上にある(図(1),(2))と言えます。また、2つ目の条件を満たすとき、直線PTは円の接線である(図(3))と言えます。
線分の長さの関係を①式や②式で表せるとき、点が円周上にあることや直線が円の接線であることが成り立つのが方べきの定理の逆です。
方べきの定理やその逆の成り立ちを知るために、実際に証明してみましょう。
方べきの定理の証明
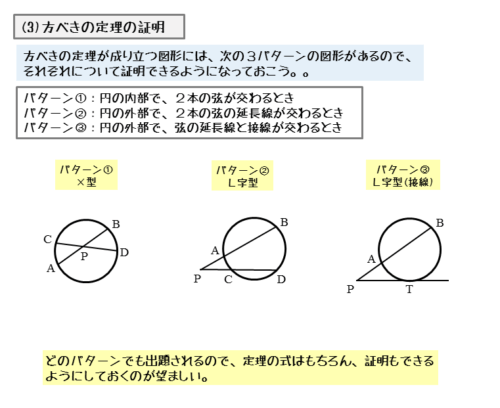
方べきの定理が成り立つ図形は、上述のように3パターンあります。
細かく分類すれば3パターンですが、線分(直線)の交わる様子で分類すればX型とL型の2パターンになります。自分なりの覚え方で良いので、図形の様子をしっかり覚えましょう。
2本の弦が円の内部で交わるとき
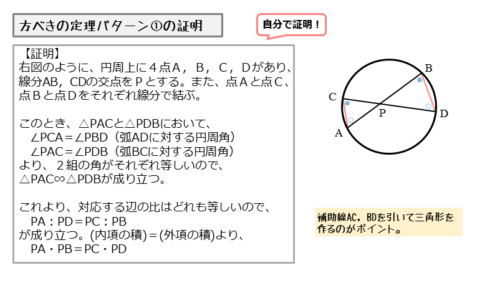
パターン①の図は、2本の弦が円の内部で交わる図です。
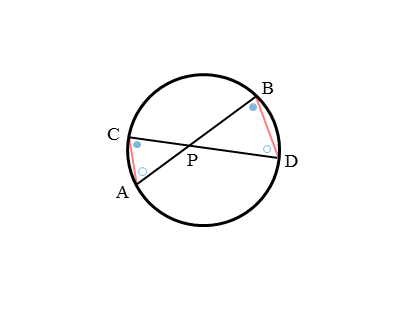
自分で作った△PACと△PDBに注目します。
パターン①の証明 1⃣
円周角の定理より
\begin{align*} &\quad \angle PAC = \angle PDB \\[ 7pt ] &\quad \angle PCA = \angle PBD \end{align*}よって
\begin{align*} \quad \triangle PAC \ \text{∽} \ \triangle PDB \end{align*}△PACと△PDBが相似な図形であることが分かりました。相似な図形では、対応する辺の比は3組とも等しくなります。このことを利用して、比例式から方べきの定理の式を導きます。
パターン①の証明 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \triangle PAC \ &\text{∽} \ \triangle PDB \end{align*}対応する辺の比は等しいので
\begin{align*} \quad PA:PD = PC:PB \end{align*}内項の積と外項の積より
\begin{align*} \quad PA \cdot PB = PC \cdot PD \end{align*}ポイントと証明の例をまとめると以下のようになります。
2本の弦の延長線が円の外部で交わるとき
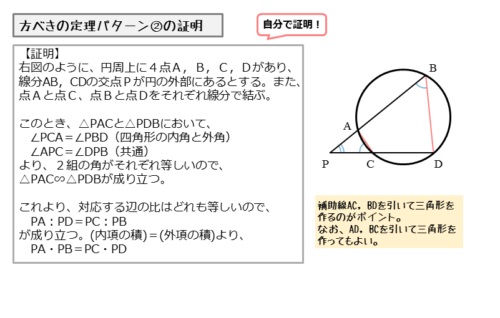
パターン②の図は、2本の弦の延長線が円の外部で交わる図です。
4点A,B,C,Dが円周上にあり、2本の弦AB,CDの延長線が円の外部で交わるとき、その交点をPとします。
このとき、AとC、BとDをそれぞれ線分で結んで、△PACと△PDBを作ります。
自分で作った△PACと△PDBに注目します。
パターン②の証明 1⃣
円に内接する四角形の性質より
\begin{align*} \quad \angle PCA = \angle PBD \end{align*}また
\begin{align*} \quad \angle APC = \angle DPB \ \text{(共通)} \end{align*}よって
\begin{align*} \quad \triangle PAC \ \text{∽} \ \triangle PDB \end{align*}△PACと△PDBが相似な図形であることが分かりました。先ほどと同じ要領で、比例式から方べきの定理の式を導きます。
パターン②の証明 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \triangle PAC \ &\text{∽} \ \triangle PDB \end{align*}対応する辺の比は等しいので
\begin{align*} \quad PA:PD = PC:PB \end{align*}内項の積と外項の積より
\begin{align*} \quad PA \cdot PB = PC \cdot PD \end{align*}パターン①と同じように相似な三角形ができるので、その関係を利用して式を導出します。
ポイントと証明の例をまとめると以下のようになります。
弦の延長線と接線が円の外部で交わるとき
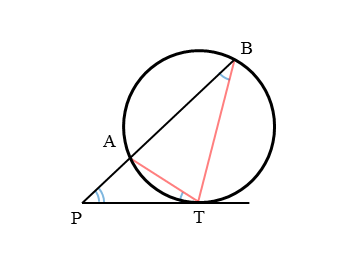
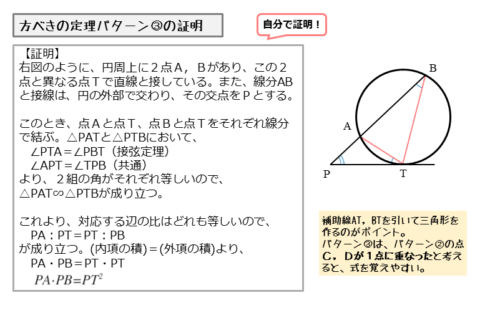
パターン③の図は、弦の延長線と接線が円の外部で交わる図です。
3点A,B,Tが円周上にあり、弦ABの延長線が、点Tにおける接線と円の外部で交わるとき、その交点をPとします。
このとき、AとT、BとTをそれぞれ線分で結んで、△PATと△PTBを作ります。
自分で作った△PATと△PTBに注目します。
パターン③の証明 1⃣
接弦定理より
\begin{align*} \quad \angle PTA = \angle PBT \end{align*}また
\begin{align*} \quad \angle APT = \angle TPB \ \text{(共通)} \end{align*}よって
\begin{align*} \quad \triangle PAT \ \text{∽} \ \triangle PTB \end{align*}△PATと△PTBが相似な図形であることが分かりました。先ほどと同じ要領で、比例式から方べきの定理の式を導きます。
パターン③の証明 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \triangle PAT \ &\text{∽} \ \triangle PTB \end{align*}対応する辺の比は等しいので
\begin{align*} \quad PA:PT = PT:PB \end{align*}内項の積と外項の積より
\begin{align*} \quad PA \cdot PB = {PT}^2 \end{align*}このパターンでも相似な三角形ができるので、その関係を利用して式を導出します。
ポイントと証明の例をまとめると以下のようになります。
パターン③はパターン②の派生
なお、パターン③の式はパターン②の派生と考えると覚えやすいでしょう。
パターン③では、パターン②の弦CDが接線になったとすると、2点C,Dがともに点Tになったと捉えることができます。これに合わせてパターン②の式でC,DをそれぞれTに置き換えると、パターン③の式になります。
C,DをTに置き換える
\begin{align*} \quad PA \cdot PB = PC \cdot PD \end{align*}において、$C \ , \ D$ を $T$ に置き換えると
\begin{align*} \quad PA \cdot PB = PT \cdot PT \end{align*}よって
\begin{align*} \quad PA \cdot PB = {PT}^2 \end{align*}以上のことから分かるように、どの条件であっても相似な三角形の関係から方べきの定理の式が導出されています。ですから、相似な三角形を見つけて比例式を立式できれば、方べきの定理を利用していることになります。
また、証明を一度でもやっていれば、方べきの定理が比例式から始める計算を省略するための手段だと分かります。最悪、方べきの定理を覚えていなくても、比例式を立式して変形していけば対応できることも分かるでしょう。
ただ、比例式から始めなくて良いぶん、やはり方べきの定理の方が計算過程を少なくなります。ですから、方べきの定理を使えないよりも使えた方が良いのは確かです。
ところで、図形の相似に注目する問題は入試でも出題されています。
方べきの定理が相似の応用だと知っていれば、相似の話が出てきても違和感を持ちませんが、式の暗記だけで済ませている人は面喰うかもしれません。公式や定理の成り立ちを知っておくことは、入試対策を行う上でも重要だと言えそうです。
方べきの定理の式は、相似な三角形の対応する辺の比から得られる式。
次は方べきの定理の逆を証明してみましょう。