図形の性質|接線と弦について

今回は接線と弦について学習しましょう。接線と弦を扱った問題であれば、必ずと言って良いほど出題される定理が出てきます。
これまでと同じように図形とセットで定理を覚えましょう。そして、図形を見たときに定理を利用可能かを瞬時に判断できるようになっておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
接線と弦
この単元で学習する事項は主に2つあります。
接線と弦に関する基本事項
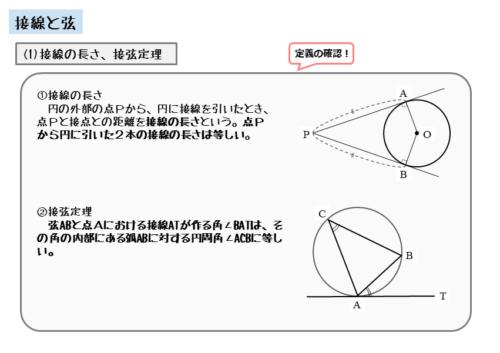
- 接線の長さ
- 接弦定理
接線の長さとは、円の外部の1点と接点との距離のことです。ですから、円の外部の1点から円に接線を引いたときの話になります。
円の外部の1点から円の接線を2本引くことができます。このとき、接線の長さはともに等しくなります。この性質については、すでに内心の単元で触れられています。
また、接弦定理とは、接点を通る弦と接線とがつくる角は、その角の内部にある弧に対する円周角と等しくなるという定理です。その角の内部にある弧とは、弦によって円周が2つの弧に分けられたときの、弦と接線に挟まれた弧を指します。
次は性質や定理が成り立つことを確認してみましょう。
接線の長さが等しいことを証明しよう
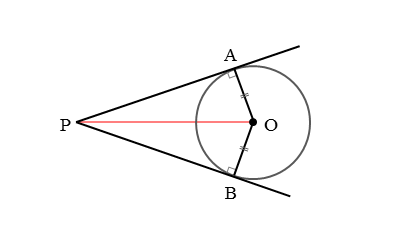
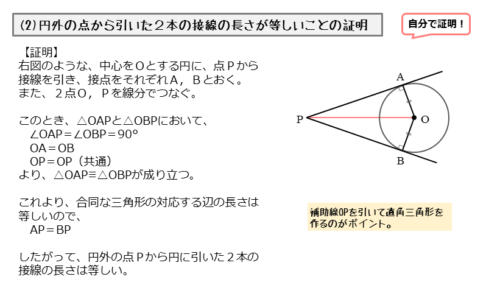
中心をOとする円に、円の外部にある点Pから接線を2本引きます。このとき、2本の接線と円との交点(接点)ができるので、それぞれA,Bとします。
また、2点A,Bを中心Oと線分で結びます。さらに、2点O,Pを線分で結ぶと、2つの三角形△OAP,△OBPができます。
△OAPと△OBPに注目します。
△OAPと△OBPの関係
$\triangle OAP$ と $\triangle OBP$ において
\begin{align*} \quad AP \perp OA \ , \ BP \perp OB \end{align*}より、$\triangle OAP$ と $\triangle OBP$ は直角三角形。
ここで
\begin{align*} &\quad OA = OB \\[ 7pt ] &\quad OP = OP \end{align*}が成り立つので
\begin{align*} \quad \triangle OAP \equiv \triangle OBP \end{align*}よって
\begin{align*} \quad AP = BP \end{align*}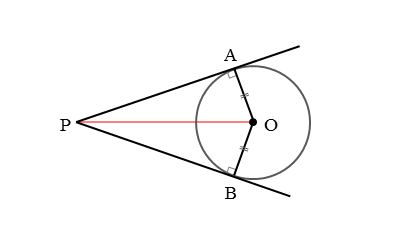
△OAPと△OBPは合同な三角形になります。辺AP,BPの長さが等しくなるので、接線の長さも等しくなります。接線の長さが等しいことの証明は、直角三角形の合同証明で行います。
次は、接弦定理が成り立つことを証明してみましょう。
接弦定理を証明しよう
接弦定理を証明する前に、角の大きさについて確認しておきます。一般に、角の大きさは3つに分類されます。
角の大きさの分類は3パターン
- 鋭角(90°未満の角)
- 直角(90°)
- 鈍角(90°を超える角)
この3つの分類を考慮すると、3つの場合に分けて接弦定理を証明する必要があることが分かります。
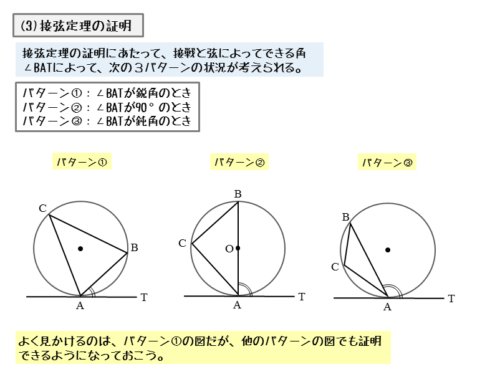
接弦定理の証明は3パターンの場合分け
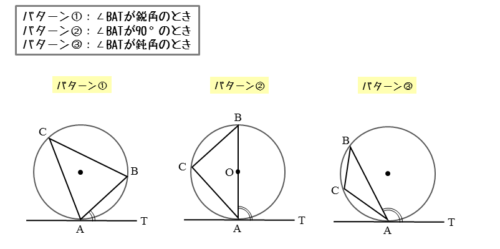
- 接点を通る弦と接点とがつくる角が鋭角のとき
- 接点を通る弦と接点とがつくる角が直角のとき
- 接点を通る弦と接点とがつくる角が鈍角のとき
それぞれのパターンで接弦定理が成り立つか、自分で実際に証明してみましょう。
タネを知ってしまえば大したことではありませんが、初見では意外と難しいので、力試しに挑戦してみると良いでしょう。
接点を通る弦と接点とがつくる角が鋭角のとき
円の周上に3点A,B,Cがあり、点Aで直線と接しています。また、接線上には点Aのほかに点Tがあります。このとき、接点を通る弦ABと接線ATとがつくる角は∠BATです。
∠BATが鋭角のとき、接弦定理が成り立つことを証明します。ただし、このままでは証明できないので、少し手を加えます。接点Aを通る直径を引き、これと円との交点をDとします。
まず、△ABDに注目します。
△ABDに注目
$\triangle ABD$ において、直径 $AD$ に対する円周角より
\begin{align*} \quad \angle ABD = 90^{\circ} \end{align*}これと三角形の内角の和より
\begin{align*} \quad \angle ADB = 90^{\circ} – \angle BAD \quad \cdots \text{①} \end{align*}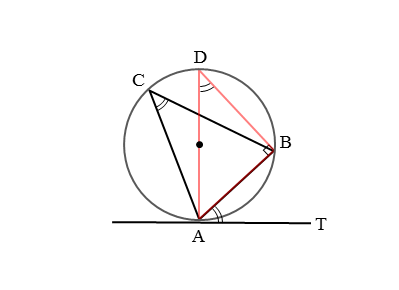
次は、直径ADと接線に注目します。
直径ADと接線に注目
$AD \perp AT$ より
\begin{align*} \quad \angle DAT = 90^{\circ} \end{align*}ここで
\begin{align*} \quad \angle DAT = \angle BAD + \angle BAT \end{align*}より
\begin{align*} \quad \angle BAT = 90^{\circ} – \angle BAD \quad \cdots \text{②} \end{align*}
①,②式から∠ADBと∠BATの関係を導くことができます。
∠ADBと∠BATの関係を導く
\begin{align*} &\quad \angle ADB = 90^{\circ} – \angle BAD \quad \cdots \text{①} \\[ 7pt ] &\quad \angle BAT = 90^{\circ} – \angle BAD \quad \cdots \text{②} \end{align*}①,②より
\begin{align*} \quad \angle ADB = \angle BAT \quad \cdots \text{③} \end{align*}
さいごに、弧ABに対する円周角に注目します。
弧ABに対する円周角に注目
$\angle ACB \ , \ \angle ADB$ は $\stackrel{ \Large \frown }{ AB }$ に対する円周角より
\begin{align*} \quad \angle ACB = \angle ADB \quad \cdots \text{④} \end{align*}③,④より
\begin{align*} \quad \angle ACB = \angle BAT \quad \cdots \text{⑤} \end{align*}
∠BATは、接点を通る弦ABと接線とがつくる角です。また、∠ACBは、∠BATの内部にある弧ABに対する円周角です。
⑤式から、接点を通る弦と接線とがつくる角が鋭角のとき、接弦定理が成り立つことを証明できました。
接点を通る弦と接線とがつくる角が直角のとき
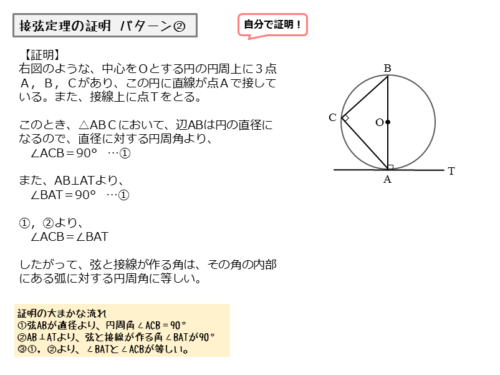
円の周上に3点A,B,Cがあり、点Aで直線と接しています。また、接線上には点Aのほかに点Tがあります。このとき、接点を通る弦ABと接線ATとがつくる角は∠BATです。
∠BATが直角のとき、接弦定理が成り立つことを証明します。なお、この証明では、直角がすでにできているので、補助線を加える必要はありません。
△ABCに注目
$\triangle ABC$ において、直径 $AB$ に対する円周角より
\begin{align*} \quad \angle ACB = 90^{\circ} \quad \cdots \text{①} \end{align*}また、$AB \perp AT$ より
\begin{align*} \quad \angle BAT = 90^{\circ} \quad \cdots \text{②} \end{align*}①,②より
\begin{align*} \quad \angle ACB = \angle BAT \quad \cdots \text{③} \end{align*}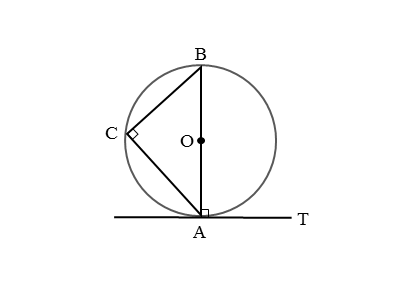
③式から、接点を通る弦と接点とがつくる角が直角のとき、接弦定理が成り立つことを証明できました。
接点を通る弦と接線とがつくる角が鈍角のとき
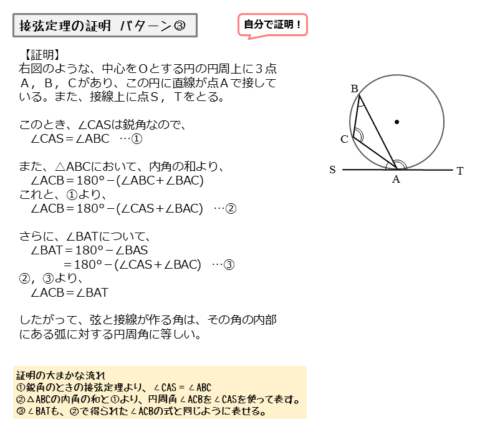
円の周上に3点A,B,Cがあり、点Aで直線と接しています。また、接線上には点Aのほかに点Tがあります。このとき、接点を通る弦ABと接線ATとがつくる角は∠BATです。
∠BATが鈍角のとき、接弦定理が成り立つことを証明します。ただし、このままでは証明できないので、少し手を加えます。接線上に接点Aに関して点Tと反対側に点Sを取ります。
まず、∠CASに注目します。∠CASは接点Aを通る弦ACと接線とがつくる角です。∠CASは鋭角になりますが、このとき接弦定理が成り立つことはすでに証明されています。
∠CASに注目
$\angle BAT$ が鈍角であるので、$\angle CAS$ は鋭角。
このとき、$\angle CAS$ について接弦定理が成り立つので
\begin{align*} \quad \angle CAS = \angle ABC \quad \cdots \text{①} \end{align*}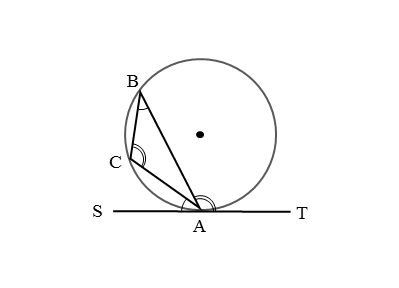
次は、△ABCに注目します。
△ABCに注目
$\triangle ABC$ において、内角の和より
\begin{align*} \quad \angle ACB = 180^{\circ} – ( \angle ABC + \angle BAC ) \end{align*}これと①より
\begin{align*} \quad \angle ACB = 180^{\circ} – ( \angle CAS + \angle BAC ) \quad \cdots \text{②} \end{align*}
さいごに、∠BATに注目します。
∠BATに注目
\begin{align*} \quad \angle CAS + \angle BAC + \angle BAT = 180^{\circ} \end{align*}であるので
\begin{align*} \quad \angle BAT = 180^{\circ} – ( \angle CAS + \angle BAC ) \quad \cdots \text{③} \end{align*}②,③より
\begin{align*} \quad \angle ACB = \angle BAT \quad \cdots \text{④} \end{align*}
④式から、接点を通る弦と接点とがつくる角が鈍角のとき、接弦定理が成り立つことを証明できました。この証明では、接点を通る弦と接線とがつくる角が鋭角のときに接弦定理が成り立つことを利用するので注意しましょう。
接弦定理を利用するときの注意点
接弦定理は、証明から分かったように、接点を通る弦と接線とがつくる角の大きさによらず成り立ちます。
また、接弦定理は、接点を通る弦の本数に合わせて、大きさの等しい角の組が存在します。
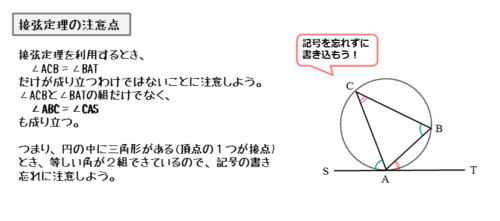
たとえば、△ABCの外接円があり、外接円と直線とが頂点Aで接しているとします。このとき、接点Aを通る弦はAB,ACの2本あるので、それぞれの弦で接弦定理が成り立ちます。
三角形の外接円で成り立つ接弦定理
弦 $AB$ において、接弦定理より
\begin{align*} \quad \angle ACB = \angle BAT \end{align*}弦 $AC$ において、接弦定理より
\begin{align*} \quad \angle ABC = \angle CAS \end{align*}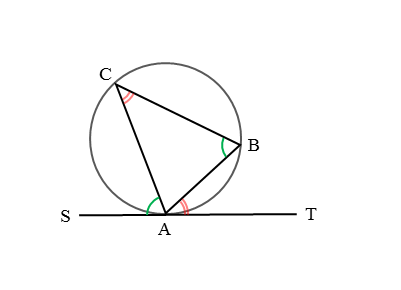
大きさの等しい角が2組できます。どちらの組にも記号を入れて、見落とさないようにしましょう。
次は接線や弦を扱った問題を実際に問題を解いてみましょう。