図形の性質|内心について

今回は内心について学習しましょう。内心も図形を扱った問題では外心と同じくらい頻出です。内心のもつ性質やそれに関わる公式などを使いこなせるようにしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
内心について
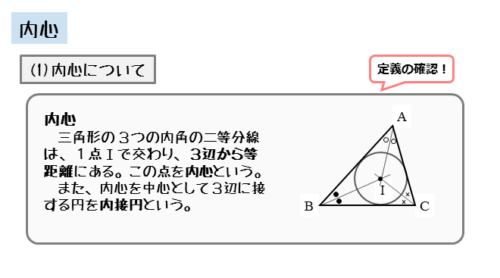
内心とは、三角形に内接する円の中心のことです。また、三角形に内接する円のことを内接円と言います。
円が三角形に内接するとき、内接円は三角形の3辺と1点で交わります。
内心の作図の仕方を覚えておきましょう。
三角形には3つの内角があります。3つの内角の二等分線をそれぞれ描くと、交点ができます。この交点が内心です。
また、交点を中心にして、三角形の辺に接するように円を描くと、三角形の内接円を描くことができます。
内心を作図してみると、その性質が分かってきます。内角の二等分線を引いたので、内心は三角形の辺から等しい距離にあります。
これは角の二等分線上の点が、角をつくる辺から等距離にあるという性質をもつからです。ですから、外心と接点の距離は、内接円の半径に等しくなります。
内心は内角の二等分線の交点。また、内心と接点の距離は、内接円の半径に等しい。
内心や内接円と関わりのある事柄
内心や内接円と関わりのある事柄は主に3つあります。内心や内接円を扱った問題のパターンと考えても良いかもしれません。
内心や内接円と関わりのある事柄
- 内角の二等分線
- 角の二等分線と比の関係
- 内接円の半径と三角形の面積の関係
内角の二等分線
△ABCにおいて内心をIとします。内心Iは内角の二等分線の交点です。
この内心Iによって、どんな関係が成り立つのかを確認しておきましょう。
△ABCの3辺は内接円に接しているので、それぞれ内接円の接線になっています。
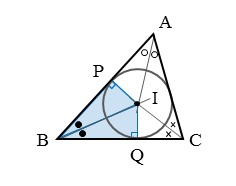
たとえば、辺AB,BCは点P,Qで内接円にそれぞれ接しています。
△IBPと△IBQに注目します。線分IPは内心Iと辺ABの間の距離、線分IQは、内心Iと辺BCの間の距離です。これらはともに内接円の半径です。
また、線分IP,IQは、円の中心と接点を結んだ線分であるので、接線である辺AB,BCに対して垂直です。ですから、△IBPと△IBQは直角三角形です。
その他にも共通の辺BIをもっていたり、内角の二等分線でできた∠IBPと∠IBQが等しかったりします。以上のことから、△IBPと△IBQは合同な直角三角形です。
同じように考えると、内角の二等分線によって、△ABCの内部に3組の合同な直角三角形ができることが分かります。
さらに、△IBPと△IBQが合同であることから、BP=BQが成り立ちます。このことは、円外の点Bから、円に2本の接線BP,BQが引かれていることからも明らかです。
したがって、2つの線分BP,BQはともに等しくなります。このことを利用した問題は頻出です。
内心があれば、三角形の内部には3組の合同な直角三角形ができる。円外の1点から円に対して2本の接線が引いてあれば、直角三角形を作ろう。
角の二等分線と比の関係
角の二等分線と比の関係は既に学習済みです。
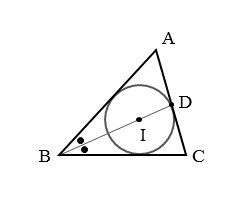
図の△ABCにおいて、角の二等分線と比の関係から、BA:BC=AD:DCが成り立ちます。
内心では角の二等分線が関係するので、BA:BC=AD:DCを利用する問題がよく出題されます。このとき、自分で点Dを作図する場合が多いのが特徴です。
作図のときに注意したいのは「点Dが接点に一致するとは限らない」ということです。
図の△ABCにおいて、角の二等分線と比の関係から、BA:BC=AD:DCが成り立ちます。
△ABDと△CBDにおいて、基本的にBA≠BCまたは∠BAD≠∠BCDであるので、合同な三角形でないことは明らかです。
もし、BA=BCまたは∠BAD=∠BCDであれば、∠BDA=∠BDC=90°が成り立ちます。このときであれば、点Dは接点に一致します。
二等辺三角形の頂角の二等分線は、底辺の垂直二等分線。△ABCがBA=BCの二等辺三角形や正三角形であれば、点Dは接点に一致。
△ABDと△CBDが合同でなければ、点Dは接点に一致しないので注意しましょう。何の根拠もなく一致すると思い込んでいる人が意外と多いので、一度は自分で作図して確かめておきましょう。
内接円の半径と三角形の面積の関係
三角形に円が内接するとき、内接円の半径を利用して、三角形の面積を表すことができます。このことは既に学習済みです。
三角形の面積を求めるとき、内接円が関わっていれば公式を優先的に使いましょう。
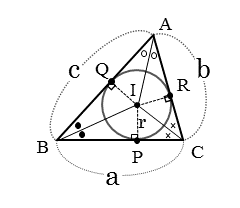
公式の導出では、内角の二等分線によって、△ABCが3つの三角形△IBC,△ICA,△IABに分割されたと考えるのがポイントです。
このとき、△ABCの面積は3つの三角形の和で表されます。内接円の半径を用いて、三角形の面積を表してみましょう。
△ABCの面積を3辺の長さと内接円の半径で表す
$BC=a \ , \ CA=b \ , \ AB=c \ , \ IQ=IR=IP=r$ とする。
\begin{align*} \triangle ABC &= \triangle IBC + \triangle IAC +\triangle IAB \\[ 7pt ] &= \frac{1}{2} \cdot BC \cdot IP + \frac{1}{2} \cdot CA \cdot IR +\frac{1}{2} \cdot AB \cdot IQ \\[ 7pt ] &= \frac{1}{2}ar + \frac{1}{2}br +\frac{1}{2}cr \\[ 7pt ] &= \frac{1}{2} r \left( a+b+c \right) \end{align*}したがって
\begin{align*} \quad \triangle ABC &= \frac{1}{2} r \left(a+b+c \right) \end{align*}△IBC,△ICA,△IABにおいて、高さがともに内接円の半径に等しく、底辺が△ABCの一辺になります。
ここでは、ほとんど出番のない事項になりますが、よく出題されます。しっかり使いこなせるようにしておきましょう。
次は内心を扱った問題を実際に解いてみましょう。