数と式｜絶対値を扱った問題を解いてみよう
絶対値の記号の使い方とその外し方を学習した後は、絶対値を扱った問題を解いてみましょう。
数や式の値の正負を吟味する
絶対値を扱った問題では、絶対値の記号に挟まれた数や式について、値の正負を吟味することが大切です。絶対値の記号を外すとき、その外し方が正の数と負の数とで異なるからです。
もし、値の正負が不明であれば、自分で場合分けすると吟味できるようになります。絶対値を考える対象が数や式のどちらであっても、値の正負をすぐに確認しましょう。
絶対値を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
$1$ は絶対値を求めよ。また、$2 \ , \ 3$ は、等式を満たす $x$ の値を求めよ。
\begin{align*} &1. \quad \left|\sqrt{3}-2 \right| \\[ 7pt ] &2. \quad \left|x \right|=5 \\[ 7pt ] &3. \quad \left|x-1 \right|=5 \end{align*}問１の解答・解説
問１
絶対値を求めよ。
\begin{align*} \quad \left|\sqrt{3}-2 \right| \end{align*}絶対値の記号を付けただけでは絶対値を求めたことにならない
問１は「絶対値を求めよ」という問題です。与式にはすでに絶対値の記号が付いているので、もう答えが出ていると思うでしょうが、そうではありません。
絶対値の記号を付けただけでは「その数や式を絶対値として扱う」という宣言をしただけで、絶対値を求めたことにはなりません。
たとえば、|－３|のように負の数に絶対値の記号を付けただけでは、絶対値３を求めたことにはなりません。
「絶対値を求めよ」と言われたら、絶対値の記号を外した形で表そう。
数や式の値の正負が自分で判断できる場合
問１では、与えられた数に絶対値の記号がついたままなので、記号を外して表します。与えられた数は多項式ですが、１つの数と見なします。
平方根は、無理数で、循環しない無限小数です。ただし、簡単なものであれば、概数で表せます。与えられた数の正負は概数から吟味できるので、絶対値の記号を外せそうです。
問１の解答例 1⃣
\begin{align*} \quad \sqrt { 3 } = 1.73 \cdots \end{align*}より
\begin{align*} \quad 1 \lt \sqrt{3} \lt 2 \end{align*}辺々に $-2$ を加えて
\begin{align*} \quad 1-2 \lt \sqrt{3}-2 \lt 2-2 \end{align*}よって
\begin{align*} \quad -1 \lt \sqrt{3}-2 \lt 0 \end{align*}与えられた数が負の数であることが分かりました。
負の数の扱いに従って、絶対値の記号を外します。
問１の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &-1 \lt \sqrt{3}-2 \lt 0 \end{align*}これより
\begin{align*} \quad &\left|\sqrt{3}-2 \right| \\[ 7pt ] = \ &-\left(\sqrt{3}-2 \right) \\[ 7pt ] = \ &-\sqrt{3}+2 \end{align*}絶対値の記号を外した後でも正の数であることが分かります。
問１のポイントと解答例をまとめると以下のようになります。
このように数や式の値の正負が判断できる場合、その正負に従って絶対値の記号を外します。
問２の解答・解説
問２
等式を満たす $x$ の値を求めよ。
\begin{align*} \quad \left|x \right|=5 \end{align*}絶対値を扱った方程式の基礎となる問題
問２は、絶対値を扱った方程式の中で基礎となる問題です。絶対値を扱った方程式では、問１の形から解を求めるのが基本的な解き方です。
公式化されている問題。絶対値の意味や方程式の意味を考えながら理解しよう。
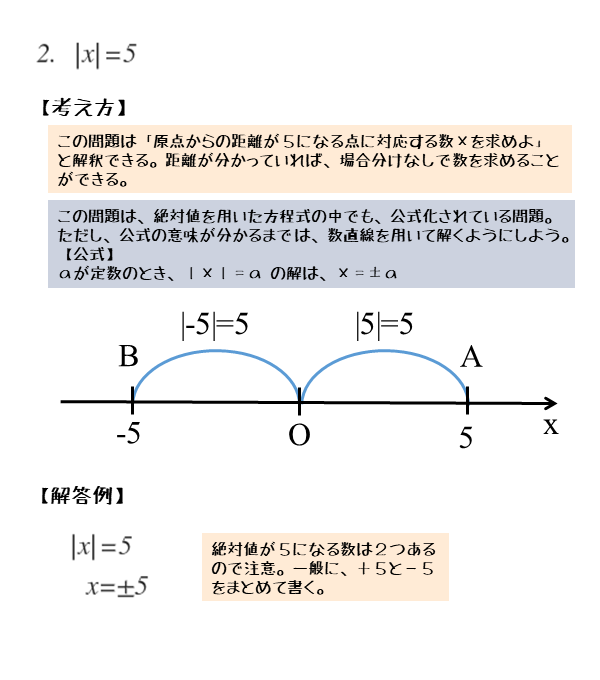
問２は「方程式を満たすｘの値を求めよ」という意味ですが、絶対値に注目すると「絶対値が５となる（点に対応する）数ｘを求めよ」と解釈することもできます。
これが方程式の意味や絶対値の意味を考えるということです。このような解釈ができれば、公式を覚えるのが楽になります。
絶対値が５となる点は、数直線上に２つあります。その点に対応する数は±５です。このことを利用して、方程式を解きます。
問２の解答例
絶対値の定義から
\begin{align*} \quad \left|x \right| &= 5 \\[ 7pt ] x &= \pm 5 \end{align*}絶対値の定義をりようすれば、方程式を解くことなく解を求めることができます。
問２のポイントと解答例をまとめると以下のようになります。
問２を場合分けで解いた場合
絶対値の定義を利用して解きましたが、ｘの値の正負を場合分けして解くこともできます。
問２の別解例
\begin{align*} &[ \ 1 \ ] \ x \geqq 0 \ \text{のとき} \\[ 5pt ] &\quad \left|x \right| = x \end{align*}より、与式は
\begin{align*} \quad \left|x \right| &= 5 \\[ 7pt ] \quad x &= 5 \end{align*}これは $x \geqq 0$ を満たす。
\begin{align*} &[ \ 2 \ ] \ x \lt 0 \ \text{のとき} \\[ 5pt ] &\quad \left|x \right| = -x \end{align*}より、与式は
\begin{align*} \quad \left|x \right| &= 5 \\[ 7pt ] \quad -x &= 5 \end{align*}よって
\begin{align*} \quad x = -5 \end{align*}これは $x \lt 0$ を満たす。
\begin{align*} &[ \ 1 \ ] \ , \ [ \ 2 \ ] \ \text{より} \\[ 5pt ] &\quad x = \pm 5 \end{align*}解を求めたら、その解が場合分けの条件を満たすことを確認しましょう。問題によっては、解が条件を満たさない場合があります。
問２のポイントと別解例をまとめると以下のようになります。
場合分けを利用した解法では、値の正負に応じて絶対値の外し方が決まっているので、機械的に解けるのが利点です。この解法は、多項式の絶対値を扱う場合に向いています。
それに対して、問２のような単項式の絶対値を扱う場合、数直線で視覚的に解く解法が向いています。
絶対値を扱った問題の解法は２パターン
- 単項式の絶対値：数直線を利用した解法（視覚的に解ける）
- 多項式の絶対値：場合分けを利用した解法（機械的に解ける）
単項式か多項式かによって、絶対値の求め方を変えよう。単項式なら数直線、多項式なら場合分け。
問３の解答・解説
問３
等式を満たす $x$ の値を求めよ。
\begin{align*} \quad \left|x-1 \right|=5 \end{align*}多項式を単項式に置き換えて解きやすい形にする
問３は、問２の単項式ｘから多項式ｘ－１に変わったので、問２と全く関係ないように感じます。しかし、多項式を１つの単項式として扱えば、問２に帰結させることができます。
絶対値が５になる点に対応する数ｘ－１を考えれば良いのですが、このままだと分かりにくいです。そこで、ｘ－１をＸに置き換えてみましょう。すると、問２と同じ形の式を導くことができます。
問３の解答例 1⃣
\begin{align*} \quad x-1=X \end{align*}とおくと、与式は
\begin{align*} \quad \left|x-1 \right| &=5 \\[ 7pt ] \left|X \right| &= 5 \end{align*}問２のｘがＸに変わっただけなので、同じ要領で方程式を解くことができます。
問３の解答例 2⃣
\begin{align*} \quad x-1 &=X \\[ 7pt ] &\vdots \\[ 7pt ] \left|X \right| &= 5 \end{align*}これを解くと
\begin{align*} \quad X = \pm 5 \end{align*}ここで $x-1=X$ より
\begin{align*} \quad x-1 = \pm 5 \end{align*}整理すると
\begin{align*} \quad x &= \pm 5+1 \\[ 7pt ] &= -4 \ , \ 6 \end{align*}絶対値の記号を外した後に注意しましょう。Ｘからもとの多項式ｘ－１に戻すのを忘れがちです。もとの多項式に戻したら、ｘについて整理して解を求めます。
問３のポイントと解答例をまとめると以下のようになります。
また、置き換えなしで解くと別解のようになります。多項式を１つのかたまりとして扱うことに慣れていれば、わざわざ置き換えずに済むでしょう。この解法の方が断然速く解けます。
最終的には、置き換えなしで解けるように演習をこなしましょう。
もちろん、場合分けを利用して解くこともできます。
問２の別解例
\begin{align*} &[ \ 1 \ ] \ x-1 \geqq 0 \ \text{すなわち} \ x \geqq 1 \ \text{のとき} \\[ 5pt ] &\quad \left|x-1 \right| = x-1 \end{align*}より、与式は
\begin{align*} \quad \left|x-1 \right| &=5 \\[ 7pt ] x-1 &= 5 \end{align*}よって
\begin{align*} \quad x = 6 \end{align*}これは $x \geqq 1$ を満たす。
\begin{align*} &[ \ 2 \ ] \ x-1 \lt 0 \ \text{すなわち} \ x \lt 1 \ \text{のとき} \\[ 5pt ] &\quad \left|x \right| = -\left(x-1 \right) \end{align*}より、与式は
\begin{align*} \quad \left|x-1 \right| &=5 \\[ 7pt ] -\left(x-1 \right) &= 5 \end{align*}よって
\begin{align*} \quad x = -4 \end{align*}これは $x \lt 1$ を満たす。
\begin{align*} &[ \ 1 \ ] \ , \ [ \ 2 \ ] \ \text{より} \\[ 5pt ] &\quad x = -4 \ , \ 6 \end{align*}入試レベルであれば、場合分けが必要な問題もあります。こちらの解法もマスターしておきましょう。
絶対値の記号がついていない残りの項は定数か
問２，３のような問題では、絶対値の定義を利用して簡単に解くことができます。場合分けしなくて済みます。
ただし、同じようにいかない問題もあります。問２，３のような解き方が可能なのは、絶対値が一定、言い換えると右辺が定数であるときです。
「右辺が定数のとき」というのは、厳密には正しい表現ではありません。正しくは「絶対値の記号がついていない、残りの項が定数であるとき」です。
右辺が定数であるとき
\begin{align*} &\quad \left|x \right| = 5 \quad \cdots \text{①} \\[ 7pt ] &\quad \left|x-1 \right| = 5 \quad \cdots \text{②} \end{align*}①，②は、ともに絶対値の記号がついていない、残りの項が定数である等式
\begin{align*} \quad \left|x \right|+3 = 5 \end{align*}は、整理すると
\begin{align*} \quad \left|x \right| = 2 \end{align*}となるので、①，②と同じ形の等式
\begin{align*} \quad \left|x \right| = x \quad \cdots \text{③} \end{align*}③は、絶対値の記号がついていない、残りの項 $x$ が定数でない等式
③式は、①，②式に似ていますが、絶対値の記号がついていない、残りの項ｘが定数でない等式です。
残りの項ｘは定数ではなく、変数です。これでは、絶対値が一定に定まりません。数直線を用いても距離を測ることができません。
絶対値を含む方程式を解くには、次の等式を基本の形にして解きます。この形であれば、場合分けなしで絶対値の記号を外すことができます。
絶対値を含む方程式の基本形
$a$ を定数とする。
このとき、$x$ の方程式
\begin{align*} \quad \left|x \right| = a \end{align*}の解は
\begin{align*} \quad x = \pm a \end{align*}絶対値記号の中のｘは、単項式でも多項式でも構いません。大事なのは、記号がついていない残りの項が定数かどうかです。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学２・Ｂや数学３では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその１『合格る計算数学１・A・２・Ｂ』
オススメその２『鉄緑会 基礎力完成 数学Ⅰ・Ａ＋Ⅱ・Ｂ』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 絶対値を扱った方程式では、基本の形を意識しよう。
- 基本の形では、絶対値の定義から数直線を利用して解く。
- 自分で場合分けをするのは、基本の形に当てはまらないとき。
- 場合分けでは、解が条件を満たすか吟味する。