中学数学|正負の数について

算数では、身長や体重、長さや面積など、身の周りの数を扱っていました。ですから扱う数の範囲は正の数だけでした。
算数から数学になると、扱う数の範囲が広がり、負の数も扱うようになります。この負の数によって、数の扱い方が大幅に変わってしまいました。
数の扱い方が変わるので、その捉え方も変える必要があります。たとえば「5-3」という式であれば、算数では減算ですが、数学では加算と捉えるのが一般的です。
算数の頃の感覚だと数学では非常に混乱するかもしれません。高校数学にどっぷりと浸かってしまう前に復習しておきましょう。
身の周りの事柄を正負の数で表す
たとえば「5m戻れ」や「10kg減った」といった表現は、正負の数を使うと上手く表すことができます。
正負の数は、正の符号(+)と負の符号(-)という対の関係にある符号を用いた数です。正の符号(+,プラス)と負の符号(-,マイナス)は、対義語の関係にある言葉を記号化したものです。
- 正の符号(+,プラス)…「進む」「増える」「大きくなる」などの言葉に対応。
- 負の符号(-,マイナス)…「戻る」「減る」「小さくなる」などの言葉に対応。
正負の数の基準は0
例に挙げた対義語を見ると分かるように、「進む」「増える」「大きくなる」「戻る」「減る」「小さくなる」などは比較するときに用いる言葉です。比較するとき、そこには基準となるものが存在します。
「5m戻れ」は、今の場所を基準として、そこから5m戻れという意味です。また「10kg増えた」は、元の体重を基準として、それから10kg増えたという意味です。
これらを正負の数では、「(今の場所から)5m戻れ」ならば「(今の場所から)-5m」、「(元の体重から)10kg増えた」ならば「(元の体重から)+10kg」と表せます。
基準から増えたり、大きくなったりする場合、正の符号(+,プラス)を使い、基準から減ったり、小さくなったりする場合、負の符号(-,マイナス)を使う。
このように身の回りの事柄に対して正負の数を用いることができます。また、身の回りの事柄では、基準となる数量はその時々で変わる場合があります。
しかし、正負の数の場合、特に指定がない限り基準となるのは0(ゼロ)となっています。
そして、0よりも大きい数を正の数と呼び、正の符号(+,プラス)を用いて表され、0よりも小さい数を負の数と呼び、負の符号(-,マイナス)を用いて表されます。
なお、0は基準であるので、正の数でも負の数でもありません。
正負の数は基準に対する相対的な数だと言えるので、算数で扱っていた絶対的な数とは異なります。このことから数の概念が変わっていることが分かります。
- +5 … 基準0よりも5だけ大きい数
- -5 … 基準0よりも5だけ小さい数
正負の数が単なる値だけでなく、文章の内容を持っています。基準よりも大きい、小さいなどの意味まで持っています。
数直線とその扱い方
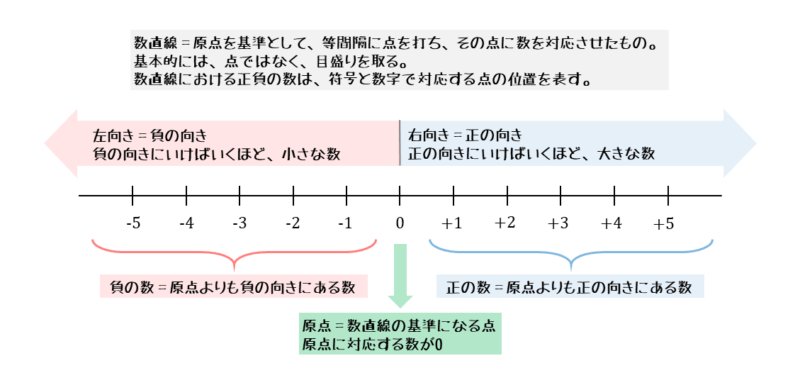
正負の数を扱うとき、数直線をよく利用します。数直線とは、等間隔の目盛りを振り、その目盛り上の点に数を対応させた直線のことです。
数直線は、点の位置を知ることができたり、数の大小を比較できたりする便利なツールです。これを応用したのがグラフのx軸やy軸です。
数直線を扱うために用語や設定があります。
数直線の設定
- 原点 … 基準となる0に対応する点のこと
- 正の向き … 原点から右の向き
- 負の向き … 原点から左の向き
左右に直線を引いたら、原点を取り、そこから左右に目盛りを振っていきます。これで数直線の完成です。一般に点ではなく目盛りを振ります。
また、原点よりも右側に正の数、左側に負の数を目盛りの点に対応させていきます。正の向きに1目盛りの点であれば+1、負の向きに2目盛りの点であれば-2といった感じで振っていきます。
目盛りに振った数を見ると、正の向きにいけばいくほど0よりも大きな数が並び、負の向きにいけばいくほど0よりも小さな数が並びます。
この設定があるので、数の大小を比較するのが容易になります。
数直線での符号と数字の意味
先ほど扱った+5や-5は、以下のような意味を持つ数です。
- +5 … 0よりも5だけ大きい数
- -5 … 0よりも5だけ小さい数
このことを数直線を使うと、以下のように向きと距離を使って表現できます。
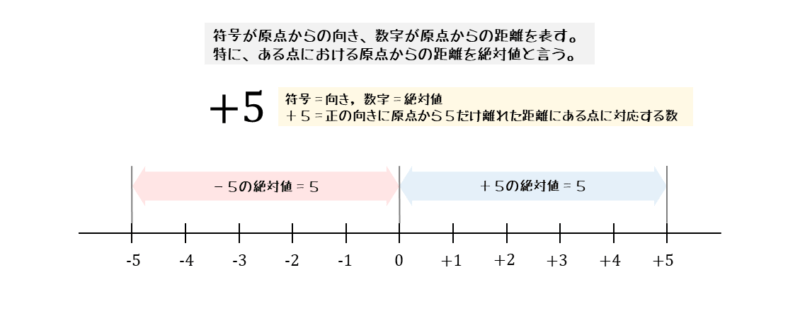
- +5 … 正の向きに、原点から5だけ離れた距離にある点に対応する数
- -5 … 負の向きに、原点から5だけ離れた距離にある点に対応する数
「0よりも大きい、小さい」という表現が、「正の向き、負の向き」に対応しています。
符号が「0よりも大きい、小さい」や「正の向き、負の向き」という意味を持っている。
また、数字は原点から+5や-5に対応する点までの距離に対応しています。この原点からある点までの距離のことを絶対値と言います。
面白いのは、+5と-5について、対応する点の位置は異なりますが、それぞれの絶対値(原点からの距離)はともに5であることです。
符号で向き、そして数字で絶対値を指定することで、点の位置を知ったり、自分で決めたりすることができるようになります(点の座標につながる)。
符号に向き、数字に絶対値という2つの意味を持たせたのが正負の数。
概念が変わったと言いましたが、ここまでの話から算数で扱っていた数とはまるで異なることが実感できたと思います。ですから、同じような捉え方や扱い方をしていては上手くいかないのは当たり前なのです。
参考 グラフのx軸とy軸について
余談になりますが、グラフではx軸とy軸という縦横の線を使います。この2つの線は数直線です。2つの数直線を互いが原点を通り、かつ直交するように用います。
2つの数直線を用いることで、平面上(2次元)にある点の位置を表すことが可能になります。位置と言っても、厳密には原点に対する相対的な位置を表します。
原点を基準とした点の位置のことを座標と言います。この座標には、x軸方向の位置であるx座標とy軸方向の位置であるy座標の2つの数を用います。
この2つの情報をセットで扱うことで、平面上の点の位置を特定できます。これと同じ考え方が地図の緯度や経度です。
数の大小
数直線を利用して、次の例題を解いてみましょう。
例題
次の数を小さい方から順に並べよ。
\begin{align} -5 \ , \ 3 \ , \ \frac{7}{2} \ , \ – \frac{1}{3} \ , \ -3 \end{align}分数は小数で表しておく
分数は計算などでは重宝しますが、大小を考えるときには使い辛いです。数の大小を考える場合、分数があれば小数で表しておきましょう。
今回は2つあり、それぞれ以下のように表せます。
分数を小数で表す
与えられた数のうち、分数を小数で表すと
\begin{align} \frac{7}{2} &= 3.5 \\[ 7pt ] -\frac{1}{3} &= -0.333\cdots \end{align}また、正の符号(+)が見当たりませんが、正の数であれば正の符号を省略することができます。本問では、下線を引いた数が正の数です。
正負に気を付ける
与えられた数のうち、正の数に下線を引くと
\begin{align} -5 \ , \ {\color{red}{ \underline{\color{black}{3}} }} \ , \ {\color{red}{ \underline{\color{black}{\frac{7}{2}}} }} \ , \ -\frac{1}{3} \ , \ -3 \end{align}数直線を書く
数の大小は数直線を利用して求めます。直線を引いて原点を取り、そこから正の向きと負の向きにそれぞれ等間隔の目盛りを振ります。
振った目盛りの下に数を書き入れます。これで数直線の準備は完了です。
与えられた数を数直線上に振っていく
与えられた数を数直線に割り振るとき、数の大小のことは考える必要はありません。ただ符号と数字だけを見て、数を数直線に割り振るだけです。
符号を見れば向きが分かります。数字を見れば絶対値が分かります。
たとえば「-5ならば、負の向きに原点から絶対値5だけ離れた位置にある点に対応する数」という感じです。小数のときはだいたいの位置に振ります。
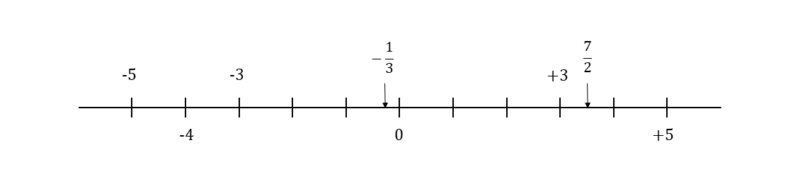
同じ要領ですべての数を数直線に割り振っていきます。与えられた数と予め数直線に振った数とが混ざらないように、与えられた数は数直線の上側に追記するのがコツです。
数直線に振った数を左から順に書く
数直線では、原点を境に右にいけばいくほど大きい数になり、左にいけばいくほど小さい数になります。
そういう設定で数直線ができているので、数を数直線に割り振ってしまえば、左から順に小さい数から大きい数へと並んだ状態になります。先ほど大小関係を考えないと言ったのは、この数直線の性質を利用しているからです。
与えられた数を並べ替えると以下のようになります。
例題の解答
数直線に並べた結果から、与えられた数を小さい順に並べると
\begin{align} -5 \ , \ -3 \ , \ -\frac{1}{3} \ , \ 3 \ , \ \frac{7}{2} \end{align}数の大小関係は「符号で向き、数字で絶対値を読み取り、数を数直線に割り振る」の手順で求める。
Recommended books
紹介するのは、高校数学の授業についていけずに焦っている人向けの教材です。授業についていけない原因は色々と考えられますが、その中でも中学で学習した内容を理解していないことが大半を占めているかもしれません。
高校1年生の場合、数学の内容はほとんどが中学の応用みたいなものです。ですから、予習が進まない、授業についていけない、などがあれば、中学の学習内容を確認することをお勧めします。確認すれば分かりますが、意外と理解していなかったことに気付くはずです。
高校2,3年生にとっては、今さら中学の復習なんかやってられないと思うかもしれません。しかし、理解できない箇所が出てくれば、嫌でも前の単元に戻らなければなりません。そうやって単元をさかのぼっていくと、結局、中学内容に行き着くことも少なくありません。
特に、苦手科目については効果的だと思います。高校での学習に行き詰っている人は、変なこだわりを捨てて、中学内容まで戻ってみると良いでしょう。案外、もっと早く取り組んでいれば良かったと思うかもしれません。
オススメ-『高校入試「解き方」が身につく問題集』シリーズ
学習内容の理解の深度を知るには、問題を解くことが一番分かりやすいです。レベル別に問題を解けば、理解度をより詳細に知ることができるでしょう。このことは、中学内容だろうと高校内容だろうと変わりません。
『高校入試「解き方」が身につく問題集』シリーズは、高校入試対策用の問題集になりますが、頻出の問題を扱っているので、重要事項やその使い方を効率良く確認することができます。
入試レベルなので応用的な問題が多いですが、高校の授業についていくにはそのくらいの理解度が必要です。つまり、高校数学についていけないとすれば、中学数学の応用レベルに達していない箇所が足枷になっている可能性が高いです。
目安としては、高校入試レベルの問題が8割以上解けることを目標にすると良いでしょう。8割取れるようになれば、高校の学習において、多少の躓きはあっても遅れを取ることは少ないでしょう。
「暗記では解けない問題の解き方」を身につける!
★「出題頻度が高い」&「解き方にコツがある」問題をマスターして得点アップ!
公立高校入試の問題は、難度の幅が広く、暗記で解ける問題と解き方(考え方)が必要な問題があります。一部の問題は演習量よりも、解き方を押さえてから演習したほうが効率的に点数を上げることができます。本書で選んだ問題をマスターすることで、入試の得点アップにつながります。
★徹底的に「解き方」に焦点を当てた解説!
「例題」「解き方チェック問題」「実践問題の解答解説」のすべてで「解き方」のチェックポイントに沿った解説をしています。
数学だけでなく、他の科目もあります。苦手科目だけでも取り組んでみると良いでしょう。
旺文社の公式サイト
ここで紹介する問題集に限りませんが、ページ数の少ない教材を選んで周回しましょう。あまり時間を掛けられないので、短期間で集中的に済ませる方が効率的です。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 正負の数は、身の周りの現象を表すのに便利な数。
- 数直線は、原点を基準として等間隔に配置された点に正負の数を対応させたもの。
- 数直線では、正負の符号は原点を基準とした向きを表す。
- 数直線では、正負の数の数字は原点からある点までの距離を表す。絶対値のこと。
- 数直線では、正負の数の大小は数直線に並べれば分かる。