整数の性質｜ｎ進法について

09/13/2023数学Ａ

今回はｎ進法について学習しましょう。日常的に用いられているのは１０進法です。ですから、２進法や５進法などで表された数の扱いには慣れていないので、意外と間違えやすい単元です。

そうは言っても、取扱いに慣れてしまえば、得点源にできる単元です。十分に演習をこなして準備しておきましょう。

ｎ進法の単元で学習すること

この単元では、以下のような事柄を学習します。

ｎ進法の単元で学習すること

ｎ進法について
記数法の変換
ｎ進法の小数
ｎ進数の四則計算
ｎ進数の各位の数と記数法の決定
ｎ進数の桁数
有限小数・無限小数、分数の小数表示と記数法

ここでは、記数法の変換までを紹介し、残りは次回以降に紹介します。

ｎ進法について

ｎ進法の基本事項

この単元で覚えておきたい用語とその定義です。

ｎ進法の基本事項

ｎ進法…位取りの基礎をｎとして数を表す方法のこと。
ｎ進数…ｎ進法で表された数のこと。
底…位取りの基礎となる数ｎのこと。
底が満たす条件…２以上の整数。
ｎ進数の各位の数字が満たす条件…０以上ｎ－１以下の整数。

特に、底や各位の数字が満たす条件は、数を決定するために用いられるので、きちんと覚えておきましょう。

また、ｎ進数の表し方にはルールがあります。ｎ進数では、底を明らかにするために、その数の右下に(n)と書くルールになっています。ただし、１０進法では、普通(10)を省略します。

ｎ進数の表し方

$2$ 進数 $\cdots \ 100_{(2)} \ , \ 234_{(2)}$

$10$ 進数 $\cdots \ 100 \ , \ 234$ （底を省略して良い）

１０進数以外では底を記述することになっているので、書き忘れないようにしましょう。ここまでがｎ進法の基本事項です。

位取り記数法

数を表すとき、通常、位取りの基礎を１０とする１０進法が用いられています。位取りとは、数の位（＝けた）を定めることや、その定め方のことです。

たとえば、１０進数で表された数12345では、基礎とした１０を用いて位取りしています。底の１０は基礎となる数なので、基数と言われることもあります。

１０進数12345は１０を用いて位取り

$\begin{align*} 12345=1 \cdot 10^{4} + 2 \cdot 10^{3} + 3 \cdot 10^{2} + 4 \cdot 10^{1} + 5 \cdot 10^{0} \end{align*}$

$\begin{align*} &1 \cdot 10^{4}& + \quad &2 \cdot 10^{3}& + \quad &3 \cdot 10^{2}& + \quad &4 \cdot 10^{1}& + \quad &5 \cdot 10^{0} \\[ 7pt ] &{\scriptsize{\text{$10^4$ の位}}}& &{\scriptsize{\text{$10^3$ の位}}}& &{\scriptsize{\text{$10^2$ の位}}}& &{\scriptsize{\text{$10^1$ の位}}}& &{\scriptsize{\text{$10^0$ の位}}} \end{align*}$

上の位から数字を抜き出して並べると $12345$

１０の累乗ごとに位が定められ、指数が大きくなるほど上の位となります。各位の数字は、上の位から順に、左から右へ並べられます。

また、各位の数字は０以上９以下の整数で、これは整数を１０で割った余りの種類と同じです。

１０進数で12345と書かれた整数について

$12345$ は各位の数字の配列を表しており、実際には

$\begin{align*} \quad 1 \cdot 10^{4} + 2 \cdot 10^{3} + 3 \cdot 10^{2} + 4 \cdot 10^{1} + 5 \cdot 10^{0} \end{align*}$

を意味する。

これと同じようにして、ｎ進数も表せます。一般にｎを２以上の整数とするとき、０以上の整数は、すべて以下の形で表すことができます。

ｎ進数はｎを用いて位取り

$\begin{align*} a_{k} \cdot n^{k} + a_{k-1} \cdot n^{k-1} + \cdots \cdots + a_{2} \cdot n^{2} + a_{1} \cdot n^{1} + a_{0} \cdot n^{0} \end{align*}$

( $a_{0} \ , \ a_{1} \ , \ a_{2} \ , \ \cdots \cdots \ , \ a_{k-1} \ , \ a_{k}$ は $0$ 以上 $n-1$ 以下の整数、 $a_{k} \neq 0$ )

これを１０進数と同じようにａ_kａ_k-1……ａ₂ａ₁ａ₀ のような数字の配列で、ｎ進数を表します。この方法を位取り記数法と言います。

ｎ＝１０のときが１０進法、ｎ＝２のときが２進法と呼ばれる表し方になります。

ｎ進数のまとめ

$n$ を $2$ 以上の整数とする。

$n$ 進法で

$\begin{align*} \quad a_{k} \ a_{k-1} \ \cdots \cdots \ a_{2} \ a_{1} \ a_{0} \end{align*}$

と書かれた $k+1$ 桁の正の整数は

$\begin{align*} \quad a_{k} \cdot n^{k} + a_{k-1} \cdot n^{k-1} + \cdots \cdots + a_{2} \cdot n^{2} + a_{1} \cdot n^{1} + a_{0} \cdot n^{0} \end{align*}$

の意味である。

ただし

$\begin{align*} \quad a_{0} \ , \ a_{1} \ , \ a_{2} \ , \ \cdots \cdots \ , \ a_{k-1} \ , \ a_{k} \end{align*}$

は $0$ 以上 $n-1$ 以下の整数、 $a_{k} \neq 0$

以上のことから分かるのは、日常的に用いられている１０進数は、あくまでも各位の数字の配列だということです。

数字の配列で四則計算ができるのかと疑問に思うでしょうが、繰り上げや繰り下げなどのルールがあるおかげで、問題なく四則計算できます。位取り記数法はすごい仕組みだと個人的には思います。

また、１０進法の小数について、小数点以下の位は以下のように定められています。

１０進数の小数：小数点以下の位

$10$ 進数の小数について、小数点以下の位は以下のように定められている。

$\begin{align*} \quad \text{$\frac{1}{10^{1}}$ の位} \ , \ \text{$\frac{1}{10^{2}}$ の位} \ , \ \text{$\frac{1}{10^{3}}$ の位} \ , \ \cdots \cdots \end{align*}$

これと同じように、ｎ進法の小数について、小数点以下の位は以下のように定められています。

ｎ進数の小数：小数点以下の位

$n$ 進数の小数について、小数点以下の位は以下のように定められている。

$\begin{align*} \quad \text{$\frac{1}{n^{1}}$ の位} \ , \ \text{$\frac{1}{n^{2}}$ の位} \ , \ \text{$\frac{1}{n^{3}}$ の位} \ , \ \cdots \cdots \end{align*}$

なお、小数については「分数と小数」の単元で詳しく紹介します。

整数の性質｜ｎ進法の小数について

記数法の変換

最も基本的な問題として、記数法の変換を扱った問題が出題されます。１０以外を底とする数に変換するには、底とした数を用いて位取りすれば良いです。

たとえば、２３を２進数に変換してみましょう。底が２であるので、２３を２で位取り、すなわち２の累乗を用いて表します。

１０進数から２進数への変換

$\begin{align*} \quad 2^{4}=16 \ , \ 2^{2}=4 \ , \ 2^{1}=2 \ , \ 2^{0}=1 \end{align*}$

より

$\begin{align*} \quad 23 = 1 \cdot 2^{4} + 0 \cdot 2^{3} + 1 \cdot 2^{2} + 1 \cdot 2^{1} + 1 \cdot 2^{0} \end{align*}$

よって、 $23$ を $2$ 進法で表すと

$\begin{align*} \quad 10111_{(2)} \end{align*}$

２３を２の累乗に分解して表します。すると各位の数字が分かります。各位の数字を並べたものが１０進数から変換した２進数です。

しかし、このやり方だとかなり面倒な作業になります。この面倒な作業を少しでも簡単に行えるのが、次に紹介する方法です。この方法の手順を覚えてしまえば機械的に変換できます。

１０進数をｎ進数で表す方法

商が０になるまでｎで割る割り算を繰り返す。
出てきた余りを逆順に並べる。

素因数分解と同じように下に割り算していきます。割る数はずっと底のままです。

また、変換するには底で割った余りを用いるので、余りを書き残しておきます。先程の２３をこの方法で２進数に変換してみます。

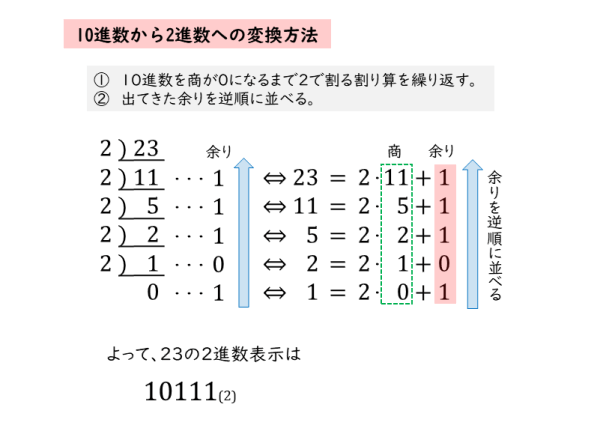
底の２で割ったときの商を下に、余りを商の横に書いていきます。商が０になったら終了です。

なお、教材によっては、余りが割る数よりも小さくなったら終了とする場合もあります。

この場合、最後の商を先頭にして余りを逆順に並べます。慣れてくると、こちらの方がやりやすいかもしれません。

10進数を2進数に変換する方法その2 — 商が割る数よりも小さくなって終了する場合

この方法では、最後の商を忘れないようにしましょう。

次はｎ進法を扱った問題を実際に解いてみましょう。

数学Ａ２進法,整数の性質,ｎ進法,底,位取り記数法,１０進法

Posted by kiri

整数の性質｜ｎ進法の小数について

整数の性質｜合同式を利用して１次不定方程式を解こう