数学A|整数の問題で合同式を使ってみよう
合同式は学習指導要領の範囲外の内容ですが、整数の問題を考えるときにとても有用なものなので、マスターしておくと吉です。
図形の合同は馴染みがありますが、整数の合同と言うとあまり聞いたことがないかもしれません。しかし、私たちの生活の中にも利用されています。
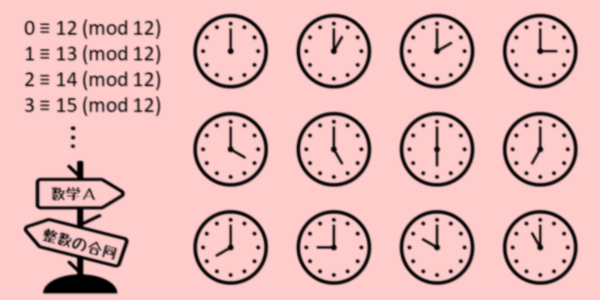
たとえば、時計の時刻は整数の合同を利用しています。時刻には24時間表記と12時間表記があります。12時間表記の場合、1時と13時は同じ時刻として扱われています。
これは12になると0にして(12を法として)数え直していると考えられます。例で挙げた1時と13時の関係を「1と13は12を法として合同」と言います。
整数の合同は、2進法や10進法などの位取り記数法にも通じるので、教科書や参考書などで一読しておいて損はないでしょう。
合同式の基本事項
合同式の基本事項は3つあります。証明については省略します。
合同式の基本事項
合同式
$a-b$ が $m$ の倍数であるとき、$a \ , \ b$ は $m$ を法として合同であるといい、$a \equiv b \pmod m$ と式で表す。このような式を合同式という。
- 合同式の性質①
- 反射律 $a \equiv a \pmod m$
- 対称律 $a \equiv b \pmod m$ のとき、$b \equiv a \pmod m$
- 推移律 $a \equiv b \pmod m \ , \ b \equiv c \pmod m$ のとき、$a \equiv c \pmod m$ または $a\equiv b \equiv c \pmod m$
- 合同式の性質② $a \equiv b \pmod m \ , \ c \equiv d \pmod m$ のとき、次のことが成り立つ。
- $a+c \equiv b+d \pmod m$
- $a-c \equiv b-d \pmod m$
- $ac \equiv bd \pmod m$
- 自然数($0$ 以上の整数も可)$n$ に対し、$a^n \equiv b^n \pmod m$
合同式を余りの関係に着目して利用する
合同式についての基本事項は上記のようになりますが、覚えておきたいのは次の関係です。
合同式で成り立つ関係
$a$ と $b$ が $m$ を法として合同であるとき、次の関係が成り立つ。
\begin{align*} \quad a \equiv b \pmod m \end{align*}⇔ $a-b$ が $m$ の倍数[ $a-b = mk$($k$ は整数)]定義
⇔($a$ を $m$ で割った余り)=($b$ を $m$ で割った余り)覚えるならココ!
定義では、2数の差a-bが法となる数mの倍数であるかどうかで合同となるかを考えています。これはこれで大切ですが、余りに注目した方が合同式をより使いやすくなります。
2数の差a-bが法となる数mの倍数であるとき、a-bはmで割り切れるので、mで割った余りは0になります。
a-bをmで割った余りが0になるには、2数a,bはmで割った余りがともに等しい数でなければなりません。
2数の差が法となる数の倍数であるとき
$a$ を $m$ で割った商と余りをそれぞれ $p_1 \ , \ r_1$ とすると
\begin{align*} \quad a=p_1 \cdot m+r_1 \end{align*}$b$ を $m$ で割った商と余りをそれぞれ $p_2 \ , \ r_2$ とすると
\begin{align*} \quad b=p_2 \cdot m+r_2 \end{align*}$2$ 数の差は
\begin{align*} \quad a-b &=\left(p_1 \cdot m+r_1 \right)-\left(p_2 \cdot m+r_2 \right) \\[ 7pt ] &=\left(p_1 -p_2 \right)m+\left( r_1 -r_2 \right) \end{align*}ここで、$a-b$ が $m$ の倍数となるのは
\begin{align*} \quad r_1 -r_2=0 \end{align*}すなわち
\begin{align*} \quad r_1=r_2 \end{align*}のときである。
したがって、$2$ 数の差 $a-b$ が $m$ の倍数になるには、$2$ 数 $a \ , \ b$ を $m$ で割った余りがともに等しくなれば良い。
この性質を利用すると、合同式を利用するときに応用が利きます。定義通りでも良いですが、余りに注目しても合同かどうかを判断することができます。
たとえば、2つの数5,8を3を法として合同かどうかを調べてみます。
定義通りに2数の差を求めると、8-5=3から2数の差は3の倍数になるので、5と8は3を法として合同です。また、この2数をそれぞれ3で割った余りはともに2になります。
具体例からも分かるように、合同である2数であれば、法とする数で割った余りがともに等しくなります。
合同式は、法となる数で割ったときの余りに着目した式とも言える。余りの等しい2つの数を≡でつなぐだけ。
このような合同式を利用して整数の問題を解いてみましょう。
合同式を利用して整数の問題を解こう
例題
$(1) \quad n$ が奇数であるとき、$n^{2}-1$ が $8$ の倍数であることを証明せよ。
$(2) \quad n$ が奇数であるとき、$n^{5}-n$ が $3$ の倍数であることを証明せよ。
$(3) \quad n$ が奇数であるとき、$n^{5}-n$ が $120$ の倍数であることを証明せよ。
例題(1)の解答・解説
例題(1)
$n$ が奇数であるとき、$n^{2}-1$ が $8$ の倍数であることを証明せよ。
例題(1)は、定石としてはn=2k+1(kは整数)とおいて解く問題です。ここでは、合同式を利用します。
例題(1)の解答例
$n$ が奇数であるので、$n$ を $8$ で割ったときの余りは
\begin{align*} \quad 1 \ , \ 3 \ , \ 5 \ , \ 7 \end{align*}のいずれかである。
よって
\begin{align*} \quad n \equiv 1 \ , \ 3 \ , \ 5 \ , \ 7 \pmod 8 \end{align*}ここで
\begin{align*} \begin{array}{c|cccc} n & 1 & 3 & 5 & 7 \\ \hline n^2 & 1 & 3^2 \equiv 1 & 5^2 \equiv 1 & 7^2 \equiv 1 \\ \hline n^{2}-1 & 0 & 0 & 0 & 0 \end{array} \end{align*}表より
\begin{align*} \quad n^{2}-1 \equiv 0 \pmod 8 \end{align*}よって、$n$ が奇数のとき、$n^{2}-1$ は $8$ の倍数である。
表の2,3行目は、合同式の性質をいくつか利用しています。
合同式の基本事項
合同式の性質①
反射律 $a \equiv a \pmod m$
合同式の性質②
$a \equiv b \pmod m \ , \ c \equiv d \pmod m$ のとき、次のことが成り立つ。
- $a-c \equiv b-d \pmod m$
- 自然数に対し $a^n \equiv b^n \pmod m$
例題(1)の別解例
別解として、指導要領内の知識で解いたときの解答例を挙げておきます(本来ならばこちらが模範解答)。
例題(1)の別解例
$n=2k+1$($k$ は整数)とおく。
\begin{align*} &n^2-1 \\[ 7pt ] = \ &\left(2k+1 \right)^2 -1 \\[ 7pt ] = \ &4k^2 +4k+1-1 \\[ 7pt ] = \ &4k \left(k+1 \right) \end{align*}$k \ , \ k+1$ は連続する $2$ つの整数であるので、いずれかは偶数、すなわち $2$ の倍数である。
よって、$4k \left(k+1 \right)$ は $2$ と $4$ を因数にもつので $8$ の倍数である。
したがって、$n$ が奇数であるとき、$n^2-1$ は $8$ の倍数である。
「(n2-1が8の倍数)=(n2-1が8を因数にもつ)」ことを示します。主に因数分解で式変形しますが、上手に変形する必要があります。
また、連続する整数の積がもつ性質についても知っておかなければなりません。これはこれでとても大切な性質なので覚えておきましょう。
合同式の場合、解答例から分かるように、式変形をほとんど必要とせず、簡潔に記述できるのが利点です。
例題(2)の解答・解説
例題(2)
$n$ が奇数であるとき、$n^{5}-n$ が $3$ の倍数であることを証明せよ。
例題(2)も例題(1)と同じように、一般的には式を変形して、与式が3を因数にもつことを示すのが定石です。ここでも合同式を利用して解きます。
例題(2)の解答例
$n$ が奇数であるので、$n$ を $3$ で割ったときの余りは
\begin{align*} \quad 0 \ , \ 1 \ , \ 2 \end{align*}のいずれかである。
よって
\begin{align*} \quad n \equiv 0 \ , \ 1 \ , \ 2 \pmod 3 \end{align*}ここで
\begin{align*} \begin{array}{c|cccc} n & 0 & 1 & 2 \\ \hline n^5 & 0 & 1^5 \equiv 1 & 2^5 \equiv 2 \\ \hline n^{5}-n & 0 & 0 & 0 \end{array} \end{align*}表より
\begin{align*} \quad n^5 -n \equiv 0 \pmod 3 \end{align*}よって、$n$ が奇数のとき、$n^5-n$ は $3$ の倍数である。
それほど難しい記述ではありません。非常にすっきりとした答案を作成できます。
例題(2)の別解例
例題(2)を指導要領内の知識で解く場合、与式を因数分解して、連続する整数の積を導出する必要があります。整数の性質を利用して解きます。
例題(2)の別解例
\begin{align*} &n^5-n \\[ 7pt ] = \ &n \left(n^4-1 \right) \\[ 7pt ] = \ &n \left(n^2-1 \right) \left(n^2+1 \right) \\[ 7pt ] = \ &\left(n-1 \right) n\left(n+1 \right) \left(n^2+1 \right) \end{align*}ここで、$\left( n-1 \right) \ , \ n \ , \ \left( n+1 \right)$ は連続する $3$ つの整数であり、この中には $3$ の倍数が含まれる。
よって、$n$ が奇数のとき、$n^5-n$ は $3$ の倍数である。
次は例題(3)ですが、その前に「連続する整数の性質」について解説します。連続する整数の性質は、整数問題では良く利用する性質です。











