数学1・A|2017センター試験・第5問を解いてみよう

第5問(2)について
第5問(2)について整理すると以下のようになります。
解答欄サシ,スセソ,タチツ
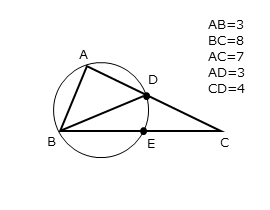
条件1
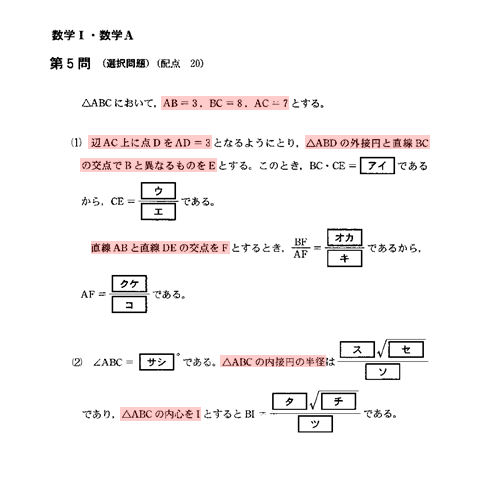
$\triangle {ABC}$ おいて、$AB=3 \ , \ BC=8 \ , \ AC=7$
このとき
$\angle {ABC}$ の値(解答欄サシ)
$\triangle {ABC}$ の内接円の半径(解答欄スセソ)
$\triangle {ABC}$ の内心を $I$ とするときの $BI$ の値(解答欄タチツ)
解答欄サシ
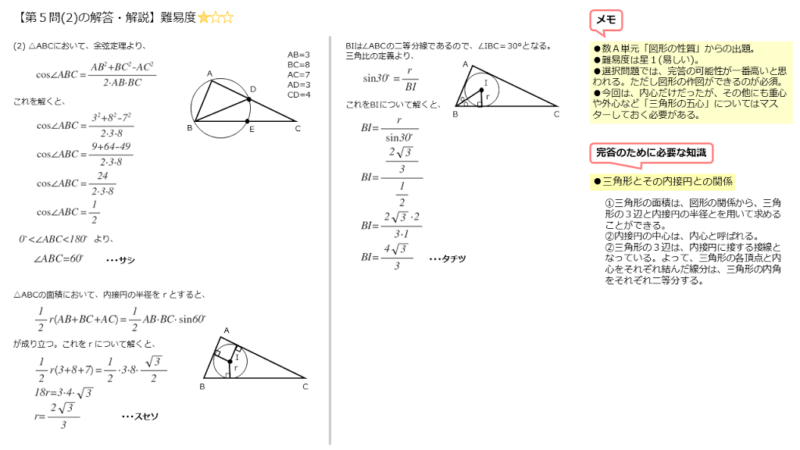
まず、∠ABCの値を求める問題です。△ABCの3辺の長さは分かっているので、迷わず余弦定理を利用します。
解答欄サシの解答例
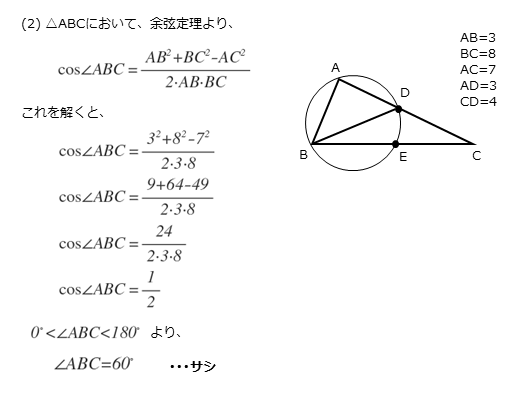
余弦定理より
\begin{align*} \quad \cos \angle ABC = \frac{{AB}^{2} + {BC}^{2} – {AC}^{2}}{2AB \cdot BC} \end{align*}ここで
\begin{align*} \quad AB=3 \ , \ BC=8 \ , \ AC=7 \end{align*}より
\begin{align*} \quad \cos \angle ABC = \frac{3^2 +8^2 – 7^2}{2 \cdot 3 \cdot 8} \end{align*}整理すると
\begin{align*} \quad \cos \angle ABC &= \frac{9+64-49}{2 \cdot 3 \cdot 8} \\[ 7pt ] &= \frac{24}{2 \cdot 3 \cdot 8} \\[ 7pt ] &=\frac{1}{2} \end{align*}$0^{\circ} \lt \angle {ABC} \lt 180^{\circ}$ より
\begin{align*} \quad \angle ABC =60^{\circ} \end{align*}余弦定理の式に線分の長さを代入した後はミスをしないように計算します。また、角の大きさの範囲に注意して∠ABCの大きさを求めます。
解答欄スセソ
次は△ABCの内接円の半径を求める問題です。
三角形の内接円の半径を求めるセオリーは、三角形の面積を利用して、内接円の半径についての方程式を導出する解き方です。
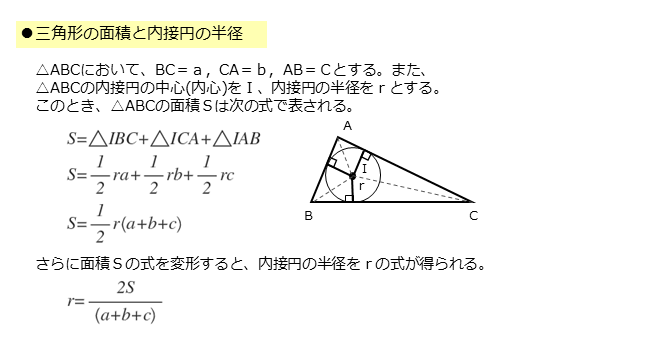
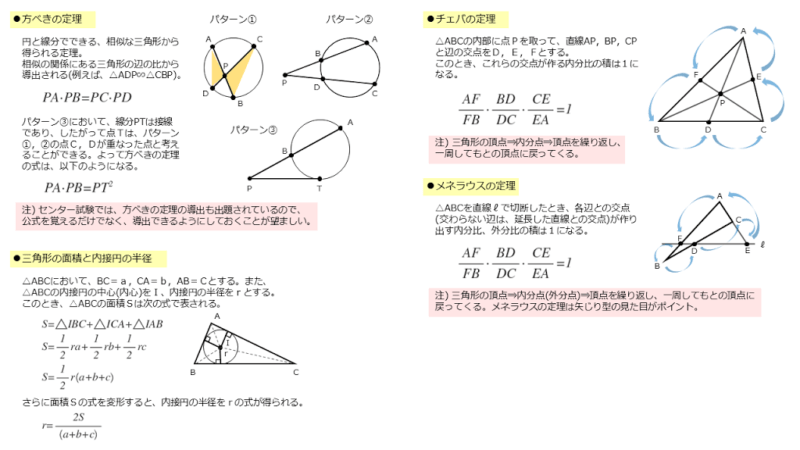
三角形の面積と内接円の半径との関係
内接円の半径を $r$ とすると、三角形の面積 $S$ は以下のように表せる。
\begin{align*} \quad S = \frac{1}{2} \ r \left( AB + BC + AC \right) \end{align*}「三角形の内接円の半径」が出てきたら「三角形の面積」を最優先で考えよう。
セオリー通りに解く場合、内接円の半径を三角形の面積から求めるので、三角形の面積を予め求めておく必要があります。
三角形の面積については公式があるので、それを利用して求めます。
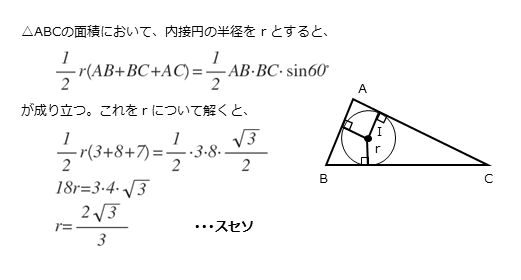
解答欄スセソの解答例
\begin{align*} &\vdots \\[ 7pt ] \quad \angle ABC &=60^{\circ} \end{align*}$\triangle {ABC}$ の面積を $S$ とすると
\begin{align*} \quad S = \frac{1}{2} \ AB \cdot BC \sin \angle ABC \end{align*}また、$\triangle {ABC}$ の内接円の半径を $r$ とすると
\begin{align*} \quad S = \frac{1}{2} r\left(AB+BC+CA \right) \end{align*}よって
\begin{align*} \quad \frac{ 1 }{ 2 } r\left(AB+BC+CA \right)= \frac{ 1 }{ 2 } \ AB \cdot BC \sin \angle ABC \end{align*}$r$ について整理すると
\begin{align*} \quad r &=\frac{AB \cdot BC}{AB+BC+CA} \cdot \sin \angle {60^{\circ}} \\[ 7pt ] &=\frac{3 \cdot 8}{3+8+7} \cdot \frac{\sqrt{3}}{2} \\[ 7pt ] &=\frac{3 \cdot 8}{18} \cdot \frac{\sqrt{3}}{2} \\[ 7pt ] &=\frac{2 \sqrt{3}}{3} \end{align*}内接円の半径をrとおいて、2つの面積の式からrについての方程式を導出します。これを解けば、内接円の半径rの値を求めることができます。
三角形の面積を内接円の半径で表す
余談になりますが、三角形の面積と内接円の半径との関係式がどのようにして導出されたのかを考えてみましょう。
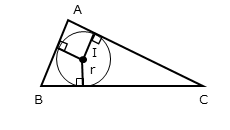
内接円の内心と三角形の頂点とを結んだ線分によって、△ABCは3つの三角形に分解できます。3つの三角形は、底辺が△ABCの一辺で、高さが内接円の半径であるような図形です。
このような3つの三角形の面積の和は、△ABCの面積に等しくなります。これで等式が得られます。
3つの三角形の高さは内接円の半径に等しいので、内接円の半径が共通因数になります。半径について式変形すると、関係式が導出されます。
解答欄タチツ
さいごは線分BIの長さを求める問題です。この問題は三角比の定義が絡んだ問題です。三角比の定義に関する問題は、意外と難しい問題なので注意が必要です。思った以上に差のつく問題です。
三角比の定義が絡んだ問題は頻出。他の単元でも定義に絡めた問題が出題されるので、定義を正しく理解しよう。
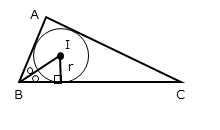
内心とは、内接円の中心のことです。内接円は三角形の3辺とそれぞれ接するので、三角形の辺上に接点ができます。
ここで、「接点・内心・三角形の頂点」の3点が頂点の三角形は直角三角形になります。
また、三角形の頂点と内心とを結ぶ線分(直角三角形の斜辺)は、三角形の内角を二等分するという性質があります。
この性質を利用すると、∠ABC=60°であるので、∠IBCの大きさを求めることができます。∠IBCと直角三角形であることを利用すれば、三角比の定義からBIの長さを求めることができます。
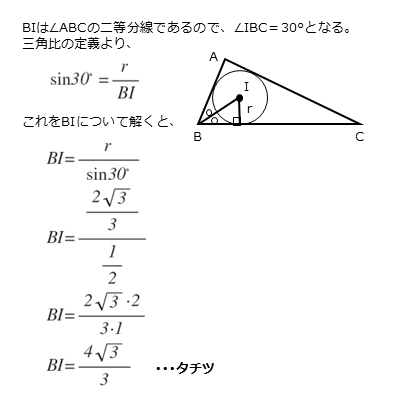
解答欄タチツの解答例
\begin{align*} &\vdots \\[ 7pt ] \quad \angle ABC &=60^{\circ} \\[ 7pt ] &\vdots \\[ 7pt ] r &=\frac{2 \sqrt{3}}{3} \end{align*}$BI$ は $\angle {ABC}$ の2等分線なので
\begin{align*} \quad \angle {IBC}=30^{\circ} \end{align*}また、三角比の定義より
\begin{align*} \quad \sin {\angle {IBC}}=\frac{r}{BI} \end{align*}$BI$ について整理すると
\begin{align*} \quad BI=\frac{r}{\sin {\angle {IBC}}} \end{align*}よって
\begin{align*} \quad BI &=\frac{\frac{2 \sqrt{3}}{3}}{\frac{1}{2}} \\[ 7pt ] &=\frac{4 \sqrt{3}}{3} \end{align*}三角比は、もともと直角三角形の2辺の関係を表すものです。正弦定理や余弦定理などの応用問題に慣れると忘れがちです。
第5問(2)のポイントと解答例をまとめると以下のようになります。
「図形の性質」に関する問題では、三角比に関わる問題も出題されますが、「三角比の拡張」が原因なのか、三角比の定義が疎かにされがちです。
三角比は直角三角形で定義されるもので、それを直角三角形以外にも拡張して利用しているだけです。(2)の最後の問題ではその辺りの関係を問われたわけですが、差がはっきりと出るので良問だと思います。
定義に関わる問題は過去にも出題されているので、しっかりと対策を立てておきましょう。暗記で済まさず、本質の理解に努めましょう。
教科書で確認しておきたい知識
- 円と線分が出てきたら、方べきの定理をイメージしよう。
- 矢じり型の図形なら、メネラウスの定理をイメージしよう。
- 三角形の内接円の半径なら、三角形の面積を利用しよう。
- 三角形の内接円の中心は内心。重心や外心なども含めて五心。
- 定義を正しく覚え、正しく利用できるようにしよう。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
共通テスト対策として必要なことをすべて備えた理想の予想問題集が完成
単に問題を解くだけでなく、その背景にある考え方や知識まで掘り下げて解説。「分析編」では、過去2回の試行調査(プレテスト)から見えてきた共通テストの出題傾向を詳細に分析するだけでなく、学習法や学習姿勢などの具体的な対策まで説明。本番でそのまま出そうな予想問題と、くわしい解説がセットになった至高の実践型問題集。
もくじ
- 本冊
- 分析編
- 解答・解説編
- 別冊
- 試行調査:2回分(2017年度/2018年度)
- 予想問題:2回分
公式サイトでは、一部の内容を閲覧できます。
KADOKAWAの公式サイト
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
Recommended books
さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。
難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。
傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。
◆特長◆大学入試の基本となる問題を扱った問題集です。問題数は138問です。問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。問題編冊子44頁、解答編冊子224頁の構成となっています。◆自分にあったレベルが選べる!◆
- 基礎レベル
- 共通テストレベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
ここで紹介する問題集は、『大学入試 全レベル問題集 数学』シリーズです。昔からある有名なレベル別問題集です。
3年の1学期までに基礎レベル1を解いて、教科書内容の補完をしてしまいましょう。夏休みになったら、共通テストレベル2で実戦練習をこなすと良いでしょう。9月~10月くらいまでにこの2冊を何度も周回して仕上げれば、秋からの2次対策にスムーズに移行できるでしょう。
なお、新入試に対応するための改訂版が2020年2月に出版されています。改訂版を希望する場合、「新入試対応」とあるものを購入しましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。