図形と計量|余弦定理について

今回は、余弦定理について学習しましょう。「正弦定理」が正弦を使った定理だったので、「余弦定理」は余弦を使った定理になるのは想像できます。
想像できることは良いことですが、どんな条件で成り立つのかを問われると答えられない人が多いです。そうならないように図と一緒に定理を考えていきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
三角比の余弦を用いた定理
余弦定理とは、その名の通り、3つある三角比のうち余弦に関する定理です。図形に関わる定理なので、作図しながら定理を確認していきましょう。
余弦定理で扱う図形は三角形だけです。正弦定理では外接円が出てきましたが、余弦定理では三角形が1つだけなので、条件に違いが付いていて覚えやすいと思います。
具体的には、三角形の3辺と、1つの内角(に対する余弦)との関係を式で表したのが余弦定理です。
この余弦定理を導出するとき、三角比の定義はもちろんですが、中学で学習した三平方の定理も利用します。式変形の力が付くので、定理の導出にぜひ挑戦してみて下さい。
余弦定理の導出
三角形の中に直角三角形を作る
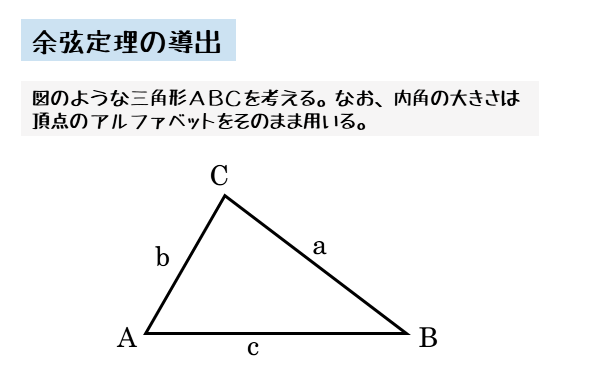
鋭角三角形を使って、余弦定理を導出してみましょう。図のような鋭角三角形(△ABC)を使います。
余弦定理の導出 1⃣
$\triangle ABC$ において
\begin{align*} &\quad \angle BAC = A \ , \ \angle ABC = B \ , \ \angle ACB = C \\[ 7pt ] &\quad AB=c \ , \ BC=a \ , \ CA=b \end{align*}とする。
鋭角三角形では三角比の定義も三平方の定理も使えないので、自分で直角三角形を作ります。
直角を作るには頂点から垂線を下ろす
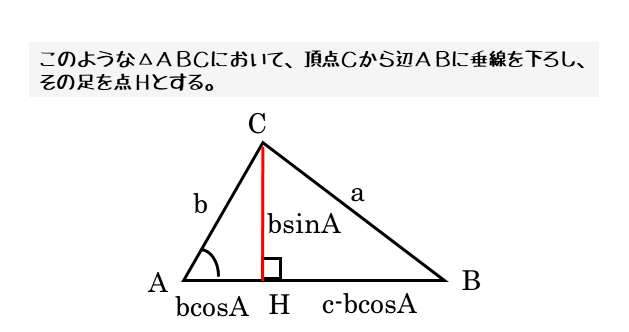
直角三角形を作るためには、直角が必要です。たとえば、頂点Cから対辺ABに垂線を下ろします。
すると、垂線と対辺ABに交点ができるので、それを点Hとします。ちなみに、この交点のことを垂線の足と言うこともあります。
垂線CHによって、△ABCの中に2つの直角三角形(△ACH,△BCH)ができます。これで三角比の定義や三平方の定理を使うことができます。
直角三角形を作るには垂線を下ろす。できた交点のことを垂線の足と言う。
△ACHの辺を三角比を使って表す
直角三角形である△ACHについて、∠Aに対する正弦と余弦を考えてみましょう。
余弦定理の導出 3⃣
$\triangle ACH$ において
\begin{align*} &\quad \sin A = \frac{CH}{AC} \quad \cdots \text{①} \\[ 7pt ] &\quad \cos A = \frac{AH}{AC} \quad \cdots \text{②} \end{align*}①より
\begin{align*} \quad CH=AC \sin A \end{align*}$AC=b$ より
\begin{align*} \quad CH=b \sin A \end{align*}②より
\begin{align*} \quad AH=AC \cos A \end{align*}$AC=b$ より
\begin{align*} \quad AH=b \cos A \end{align*}三角比の定義から、①,②式を導き、これらを辺CH,AHについてそれぞれ変形しておきます。
直角三角形の底辺や高さは、斜辺と余弦または正弦を使って表すことができる。
△BCHで成り立つ三平方の定理を使う
次に、△BCHに目を向けます。辺BHの長さは、辺AHを利用すると求めることができます。
余弦定理の導出 4⃣
$\triangle BCH$ において
\begin{align*} \quad BH = AB – AH \end{align*}$AB=c \ , \ AH=b \cos A$ より
\begin{align*} \quad BH = c-b \cos A \end{align*}三平方の定理より
\begin{align*} \quad BC^{2} = CH^{2} + BH^{2} \quad \cdots \text{③} \end{align*}△BCHは直角三角形なので、三平方の定理が成り立ちます。三平方の定理から導いた式を整理します。
余弦定理の導出 5⃣
③を整理すると
\begin{align*} &\quad a^{2} = \left(b \sin A \right)^{2} + \left(c-b \cos A \right)^{2} \\[ 7pt ] &\quad a^{2} = b^{\scriptsize{2}} \left(\cos^{2}{A} + \sin^{2}{A} \right) + c^{2} -2bc \cos A \end{align*}ここで
\begin{align*} \quad \cos^{2}{A} + \sin^{2}{A} = 1 \end{align*}より
\begin{align*} \quad a^{2} = b^{2} + c^{2}-2bc \cos A \end{align*}これで△ABCの3辺と1つの内角(に対する余弦)との関係を表す式を導出できました。これが余弦定理です。
余弦定理の導出 6⃣
③を整理すると
\begin{align*} &\quad a^{2} = \left(b \sin A \right)^{2} + \left(c-b \cos A \right)^{2} \\[ 7pt ] &\quad a^{2} = b^{2} \left(\cos^{2}{A} + \sin^{2}{A} \right) + c^{2} -2bc \cos A \end{align*}ここで
\begin{align*} \quad \cos^{2}{A} + \sin^{2}{A} = 1 \end{align*}より
\begin{align*} \quad a^{2} = b^{2} + c^{2}-2bc \cos A \end{align*}このような関係を表す式は、他の内角∠B,∠Cに対する余弦でも同じように導くことができます。その結果、1つの三角形に対して、余弦定理の式は3つあることになります。
余弦定理の式は3通り
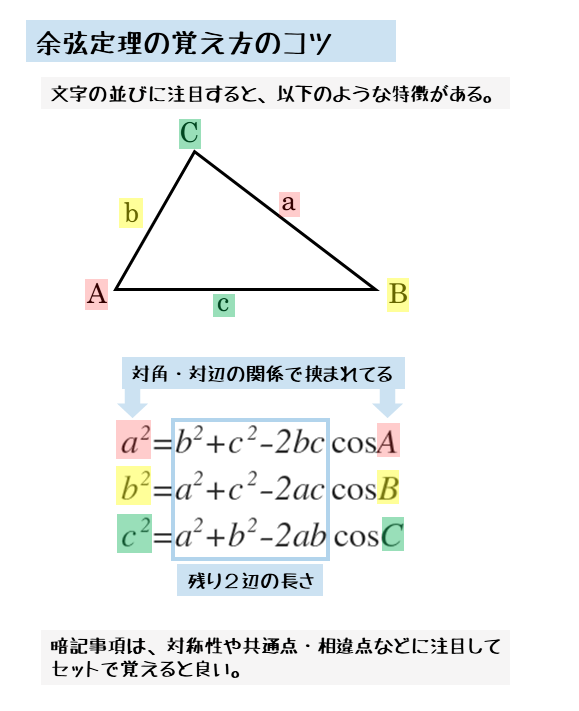
\begin{align*} &\quad a^{2} =b^{2} + c^{2} -2bc \cos A \\[ 7pt ] &\quad b^{2} =a^{2} + c^{2}-2ac\cos B \\[ 7pt ] &\quad c^{2} =a^{2} +b^{2} -2ab\cos C \end{align*}導出の仕組みが分かったら、あとは覚えるだけです。アルファベットの対応関係に注目すれば覚えやすいでしょう。
鈍角三角形でも導出できるのか
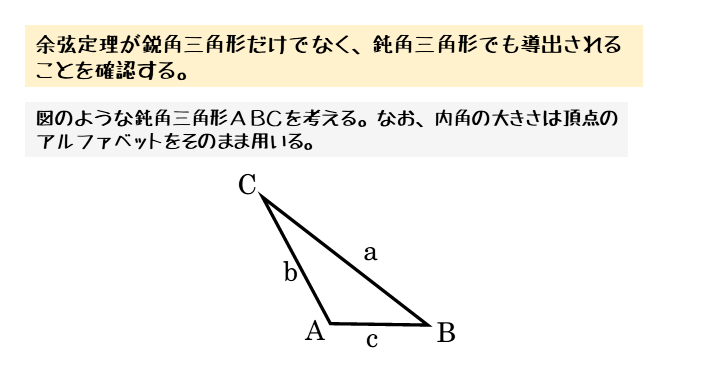
鋭角三角形で導出しましたが、鈍角三角形でも同じ式を導出できるのかを確かめてみましょう。
∠Aが鈍角である△ABCを考えます。最初に与えられている条件は以下の通りです。
鈍角三角形のときの余弦定理の導出 1⃣
$\triangle ABC$ において
\begin{align*} &\quad \angle BAC = A \ , \ \angle ABC = B \ , \ \angle ACB = C \\[ 7pt ] &\quad AB=c \ , \ BC=a \ , \ CA=b \end{align*}とする。
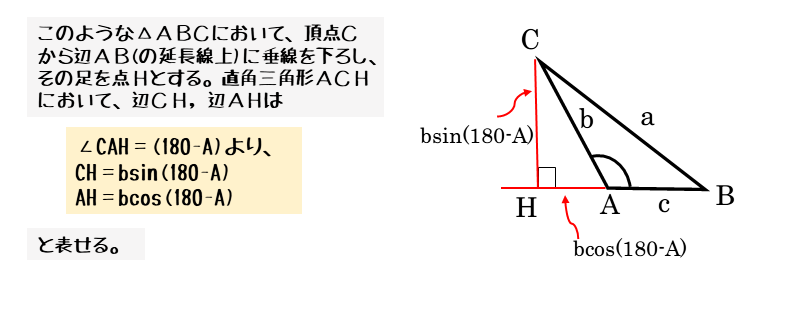
直角三角形を作るために、頂点Cから対辺ABに垂線を下ろします。このとき、頂点によっては対辺を延長する補助線を引く必要があります。
頂点Cから下した垂線の足を点Hとすると、△ACH,△BCHが直角三角形になります。先ほど同じ流れで直角三角形の辺の長さを求めていきます。
△ACHの辺の長さを三角比を使って表す
直角三角形である△ACHに注目します。このとき、∠BAC=A,∠CAH≠Aであることに注意しましょう。
∠CAHに対する正弦と余弦を考えます。
鈍角三角形のときの余弦定理の導出 3⃣
$\triangle ACH$ において
\begin{align*} &\quad \sin {\angle CAH} = \frac{CH}{AC} \quad \cdots \text{①} \\[ 7pt ] &\quad \cos {\angle CAH} = \frac{AH}{AC} \quad \cdots \text{②} \end{align*}①より
\begin{align*} \quad CH=AC \sin {\angle CAH} \end{align*}$AC=b \ , \ \angle CAH=180^{\circ}-A$ より
\begin{align*} \quad CH=b \sin \left(180^{\circ}-A \right) \end{align*}②より
\begin{align*} \quad AH=AC \cos {\angle CAH} \end{align*}$AC=b \ , \ \angle CAH=180^{\circ}-A$ より
\begin{align*} \quad AH=b \cos \left(180^{\circ}-A \right) \end{align*}三角比の定義から、①,②式を導き、これらを辺CH,AHについてそれぞれ変形しておきます。このとき、∠CAH=180°-Aであることに注意します。
どの角に対する三角比なのかを意識しよう。
さらに、三角比の拡張を利用して変形します。すると、∠Aに対する正弦や余弦を使った式が得られます。
鈍角三角形のときの余弦定理の導出 4⃣
\begin{align*} &\quad \sin \left(180^{\circ}-A \right)=\sin A \\[ 7pt ] &\quad \cos \left(180^{\circ}-A \right)=-\cos A \end{align*}より
\begin{align*} &\quad CH=b \sin A \\[ 7pt ] &\quad AH=-b \cos A \end{align*}三角比の拡張を使うのは、ここではなく、最後の方で行うこともある。解説によって異なるが早いか遅いかの違いだけ。
△BCHで成り立つ三平方の定理を使う
次に、△BCHに注目します。辺BHの長さは、辺AHを利用すると求めることができます。
鈍角三角形のときの余弦定理の導出 5⃣
$\triangle BCH$ において
\begin{align*} \quad BH = AB + AH \end{align*}$AB=c \ , \ AH=-b \cos A$ より
\begin{align*} \quad BH = c-b \cos A \end{align*}三平方の定理より
\begin{align*} \quad BC^{2} = CH^{2} + BH^{2} \end{align*}よって
\begin{align*} &\quad a^{2} = \left(b \sin A \right)^{2} + \left(c-b \cos A \right)^{2} \\[ 7pt ] &\quad a^{2} = b^{2} \left(\cos^{2}{A} + \sin^{2}{A} \right) + c^{2} -2bc \cos A \end{align*}$\cos^{2}{A} + \sin^{2}{A} = 1$ より
\begin{align*} \quad a^{2} = b^{2} + c^{2}-2bc \cos A \end{align*}2辺AH,CHは、鋭角三角形のときと同じ式で表されます。ですから、△BCHについて、三平方の定理を利用すると同じ結果になります。
鈍角三角形であっても、鋭角三角形と同じように、3辺と1つの内角(に対する余弦)の関係を表す式を導出することができます。
余弦定理の使い方
余弦定理も正弦定理と同じように、与えられる条件によって使えるときとそうでないときがあります。
余弦定理で用いられる数量をしっかりと把握しておけば、与えられた条件と照らし合わせて判断できます。
余弦定理の式を観察すると、3辺の長さと、1つの内角に対する余弦の4つの数量が用いられています。ですから、4つのうち3つの数量が与えられていれば、余弦定理を使って方程式を導くことができます。
三角形の3辺と1つの内角の関係を表す余弦定理
\begin{align*} &\quad a^{2}=b^{2}+c^{2}-2bc \cos A \\[ 7pt ] &\quad b^{2}=a^{2}+c^{2}-2ac \cos B \\[ 7pt ] &\quad c^{2}=a^{2}+b^{2}-2ab \cos C \end{align*}余弦定理を変形して使おう
辺の長さを求めるとき、3つの式から1つを選んで使います。しかし、余弦の値、または角の大きさを求めるとき、そのままだと使い勝手が悪いです。
そのようなとき、余弦定理の式を変形したものを用いることもあります。
余弦の値、または角の大きさを求めるとき
余弦定理の式を余弦について変形すると
\begin{align*} &\quad \cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc} \\[ 10pt ] &\quad \cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac} \\[ 10pt ] &\quad \cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab} \end{align*}共通点や相違点を見つけて効率よく覚えよう
公式や定理の式は、試験中に毎回導出するのは面倒なので、やはり覚えておく必要があります。そのためには、共通点や相違点などの特徴を掴むと覚えやすくなります。自分なりに工夫することが大切です。
余弦定理では、両端の文字は対角と対辺の関係になっています。その間に、残りの2辺の文字があります。
Recommended books
図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。
そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。
オススメその1
分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。
ここで紹介するのは『数学1高速トレーニング 三角比編』です。
三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。
これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。
オススメその2
『改訂版 坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。
計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。
坂田のビジュアル解説で最近流行りの空間図形までフォロー!
数学1「図形と計量」(いわゆる三角比)と数学A「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。
また、今回の改訂により、近年の大学入試(上位から下位まで幅広く)で頻出の空間図形の問題を厚くしました。
オススメその3
『中学入試 算数図形問題完全マスター』と『中学入試 算数図形問題完全マスター ハイレベル』は中学入試のための教材ですが、図形に苦手意識がある人にはちょうど良いかもしれません。
公立校の適性検査型入試問題を意識し、長文の問題や思考力・表現力を要する問題も収録されています。チャート式で有名な数研出版の教材なので、安心して取り組めるでしょう。
さいごに、もう一度、頭の中を整理しよう
- 余弦定理は、三角形の3辺と1つの内角(に対する余弦)との関係を表す。
- 余弦定理は、三角比の定義や三平方の定理を利用して導出される。
- 余弦定理の式は、1つの三角形で3つ得られる。
- 3辺と1つの内角の4つの数量のうち3つの数量が分かっていれば、余弦定理を使って方程式を作れる。