図形と計量|三角比の拡張について

三角比は、直角三角形の2辺を用いて定義されることを学習しました。
しかし、三角形は直角三角形だけではありません。他の三角形には三角比を利用できないのでしょうか。
今回は、それを解決する三角比の拡張について学習しましょう。
記事の画像が見辛いときはクリックすると拡大できます。
三角比の拡張とはどういうこと?
「三角比の拡張」という単元ですが、「拡張」とはどういうことでしょうか?
あまり難しく考えることはありません。「拡張」というのは「利用」と置き換えて良いと思います。
直角三角形では、90°以外の内角はすべて90°未満の鋭角で、その1つの鋭角に対する比の値を三角比と定義していました。
三角比の定義から考えると、直角三角形以外の三角形では無理そうです。このままでは頑張って定義したにも拘らず、三角比は限定的で、利用価値の低いものになってしまいます。
この三角比を「鋭角三角形や、90°を超える内角をもつ鈍角三角形にも利用できないか?」というのが「三角比の拡張」における出発点になります。
この点をしっかり押さえておけば、どんな三角形を扱っていても直角三角形を意識できると思います。
様々な三角形で三角比を扱うようになると、ついつい三角比の定義を忘れがちになります。三角比の拡張は、あくまでも直角三角形から得られた三角比を他の三角形で利用するお話です。
拡張のための設定を確認しよう
三角比を拡張して利用するために、予め設定された舞台があります。
三角比を利用するための舞台設定
- x軸とy軸をもつ座標平面
- 原点を中心とする半径rの円(状況によっては半円)
- 円周上の点P(x,y)
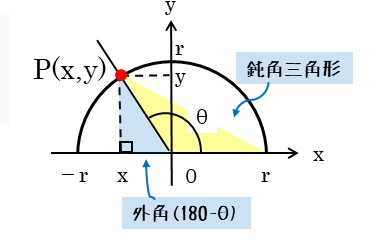
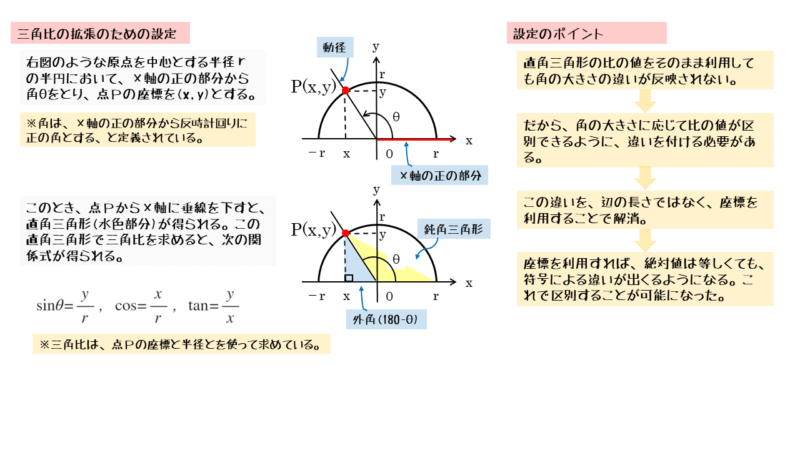
図のようなx軸とy軸をもつ平面座標に、原点を中心とする半径rの半円を図示します。
この円周上の点P(x,y)と原点Oとを結んだ線分OP(OP=r)と、x軸の正の部分とがなす角をθとします。
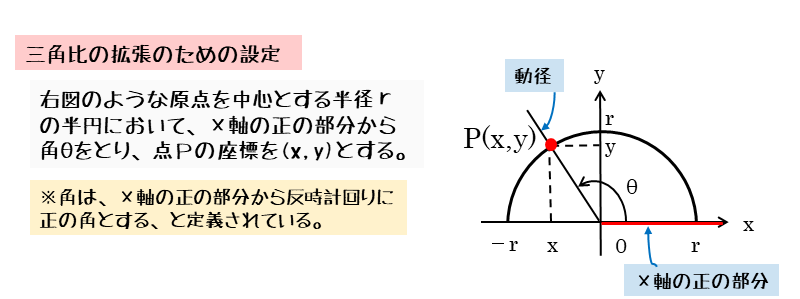
線分OPは原点を中心として動く半径なので、動径と呼ばれます。ちなみに、この動径OPが原点Oを中心に反時計回りに動く向きが正の向きと定義されています。
このような図形において、点Pを円周上で移動、あるいは動径を動かすと、角θの大きさが変化します。たとえば、動径がy軸を通り過ぎると、角θは90°よりも大きな角になります。
角θが90°を超えると鈍角になるので、三角形は鈍角三角形として扱っていることになります。鈍角三角形は、絶対に直角三角形になることはありません。
このように様々な大きさに変化する角θについて、直角三角形の三角比を利用します。これが拡張になります。
三角形の外角に注目する
角θが0°<θ<90°を満たすとき、直角三角形を作れるので、定義に当てはめて角θに対する三角比を求めることができます。
これが90°<θ<180°になると角θは鈍角になるので、三角比の定義に当てはめることができません。
しかし、鈍角の外角に注目すると、外角は90°未満の鋭角になります。この外角をもつ直角三角形に注目することで、三角比を利用することが可能になります。
たとえば、 120°の三角比の場合、外角は180°-120°=60°となるので、60°に対する三角比を利用します。
ただ、このままでは120°と60°の三角比(正弦・余弦・正接)がすべて同じになってしまうので、どちらの角に対する三角比なのか区別がつかなくなります。
この問題を解決するのが座標平面です。半径rと点Pの座標(x,y)を用いて、三角比を表します。
角θと角(180°-θ)の三角比を区別するための方法
- 直角三角形の斜辺 ⇒ 半径r
- 直角三角形の底辺 ⇒ 点Pのx座標(座標なので正負がある)
- 直角三角形の高さ ⇒ 点Pのy座標(座標なので正負がある)
このときの三角比の式は図のようになります。

長さではない座標を使って良いのか不安になりますが問題ありません。
たとえば、0°<θ<90°では点Pの座標は正の数であるので、これまで通りの三角比が得られます。
それに対して、90°<θ<180°では点Pのy座標が負の数になるので、余弦と正接の値が負の数になります。
正弦・余弦・正接のどれかだけで見れば区別がつかないかもしれません。しかし、正弦・余弦・正接の値を合わせて見れば、120°のときの三角比と60°のときの三角比とを区別することができます。
鋭角の三角比を借用して、鈍角の三角比を表す。このとき、そのまま借用するのではなく、半径と座標を使うことで区別させる。
このように座標平面で三角比を用いることで、これまでの三角比を用いて鈍角の三角比を表すことができ、また正負の符号で区別することもできます。
三角比が異なるということは、角の大きさが異なるということになるので、どの角に対する三角比かを区別することも可能になりました。これまでをまとめると以下のようになります。
今後は90°を超える鈍角の三角比を扱うようになるので、座標平面で半径と座標を使って三角比を求めるようにしよう。
次は、実際に鈍角の三角比を求めてみましょう。
実際に鈍角三角形で三角比を求めてみよう
鈍角、たとえば θ=120°のときの三角比を求めてみましょう。
座標平面で作図しよう
先ほど設定した座標平面で120°の角を作ります。必ず図示できるようになっておきましょう。
まず、原点Oを中心とする半径2の半円を描きます。
次に、角θの大きさが120°になるように、点Pと動径OPを円周上に描きます。
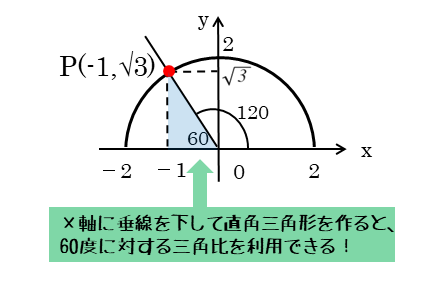
さいごに点Pからx軸に垂線を下ろして直角三角形を作ります。
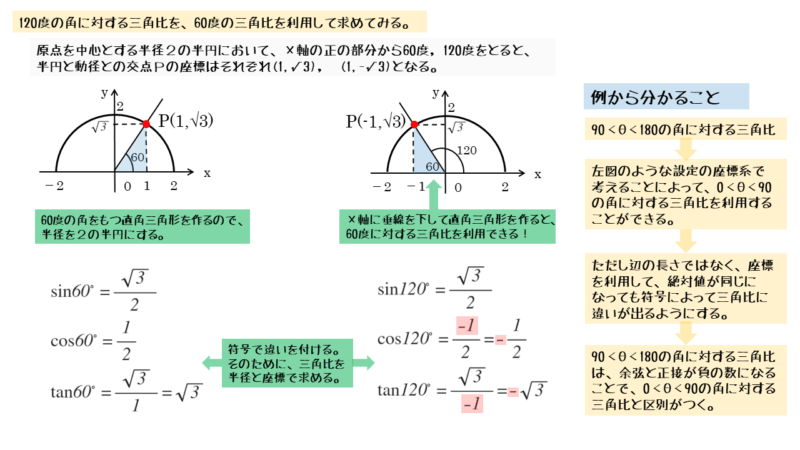
120°の外角は60°であるので、60°の内角をもつ直角三角形ができています。60°の直角三角形を利用すると、点Pの座標は(-1,$\sqrt{3}$)です。準備ができたので、三角比を求めます。
60°に対する三角比を利用するために、半径を斜辺の長さや比に相当する値にしておく。半径が2であれば、1:2:$\sqrt{3}$ の比を利用できる。
三角比は長さで求めない
90°以上の角に対する三角比を求めるとき、長さではなく、点Pの座標を用いることに注意しましょう。点Pの座標を使わないと、三角比がみな等しくなってしまいます。
半径rと点Pの座標(x,y)で表される三角比の式を用いて、三角比を求めます。
鈍角に対する三角比
半径 $r$、点P $(x \ , \ y)$ のとき
\begin{align*} \quad \sin \theta &= \frac{y}{r} \\[ 10pt ] \cos \theta &= \frac{x}{r} \\[ 10pt ] \tan \theta &= \frac{y}{x} \end{align*}具体的な角で考えてみると違いがよく分かります。
120°の三角比は、60°の三角比を利用しました。正弦・余弦・正接の値は、絶対値であればすべて等しくなりますが、座標を用いるので正負の違いが出ているので区別できます(余弦と正接)。
120°と60°の余弦と正接では、点Pのx座標が関わるので正負が異なります。このように正弦・余弦・正接のうちどれか1つでも異なれば、角の大きさも異なると考えます。
また、60°のような鋭角の三角比でも、半径と座標を用いても問題ないことが分かります。今後、座標平面で三角比を考えるようにしましょう。
角の大きさを区別するときは、正弦・余弦・正接を1セットで考えよう。どれか1つが異なれば、同じ三角形ではないということ。
覚えておきたい鋭角と鈍角の関係と、その三角比
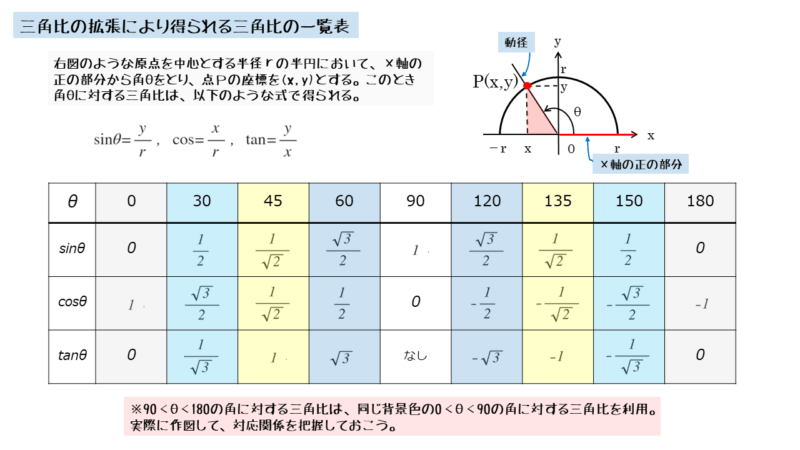
直角三角形において、3辺の比が分かるのは30°,45°,60°のときです。これらが三角比を扱うときの基本になります。これらの角と対応する鈍角をセットにして覚えましょう。
対応関係が分かるように一覧表にまとめてみました。このように一覧表を作ってみると、符号の違いが良く分って覚えやすくなります。
ちなみに0°,90°,180°のときですが、三角形としてどうなんだと思うかもしれません。
三角形ができるわけではありませんが、拡張によって三角比の値を導出することができます。三角比の拡張と言うくらいなので、三角形という図形から徐々に離れていきます。
なお、覚えておきたい三角比と紹介しましたが、「半径を決めて作図し、座標に注意して三角比を求める」という作業ができさえすれば、無理やり暗記する必要はありません。むしろ、暗記するよりも図示できることの方が応用が利きます。
今後は作図の機会が増えるので、数字を覚えることに労力を使うよりも、実際に作業しながら三角比を覚えていく方が絶対に効率的です。
Recommended books
図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。
そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。
オススメその1
分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。
ここで紹介するのは『数学1高速トレーニング 三角比編』です。
三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。
これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。
オススメその2
『改訂版 坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。
計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。
坂田のビジュアル解説で最近流行りの空間図形までフォロー!
数学1「図形と計量」(いわゆる三角比)と数学A「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。
また、今回の改訂により、近年の大学入試(上位から下位まで幅広く)で頻出の空間図形の問題を厚くしました。
オススメその3
『中学入試 算数図形問題完全マスター』と『中学入試 算数図形問題完全マスター ハイレベル』は中学入試のための教材ですが、図形に苦手意識がある人にはちょうど良いかもしれません。
公立校の適性検査型入試問題を意識し、長文の問題や思考力・表現力を要する問題も収録されています。チャート式で有名な数研出版の教材なので、安心して取り組めるでしょう。
さいごに、もう一度、頭の中を整理しよう
- 三角比の拡張では、直角三角形を利用して鈍角の三角比を求めること。
- 三角比を求めるとき、座標平面で作図して求める。
- 三角比を求めるとき、半径と座標を使うことで、鋭角の三角比を利用できる。
- 半径と座標を使うことで、絶対値が等しくても、符号の違いがついた三角比を得られる。