集合と論理|共通部分・和集合・補集合について

今回は、集合にも様々なものがあることを学習します。複数の集合を扱うので、ベン図を使って視覚的に捉えると理解しやすいでしょう。
また、新しい法則も出てくるので、しっかり使えるようにしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
物事の全体像を把握するにはやはり可視化が有効
物事の全体像を把握するのに役立つのは「可視化」です。数学で言えば、グラフや図形を描くことです。
この単元では集合やそれに属する要素を扱います。今後は先ほども述べたように複数の集合を扱います。集合を扱うにあたって、その表し方には2通りの方法がありました。
集合の表し方
その1:条件を満たす要素を書き並べる方法
その2:要素が満たす条件を述べる方法
特に、要素を書き並べる方法を使えば集合の要素を把握できるので、問題を解ける場合が多いでしょう。しかし、要素の数が多くなってくると煩雑になり、把握し辛くなるデメリットがあります。
そのような場合、要素を取りこぼす可能性が高くなります。それを防ぐのがベン図です。
ベン図で可視化することによって、「どの集合に属しているか」や「共通の要素はどれか」といったことを視覚的に把握することができます。
ミスの多い人は手を動かさないことが多い。些細なミスを防ぐために、図解して視覚化しよう。
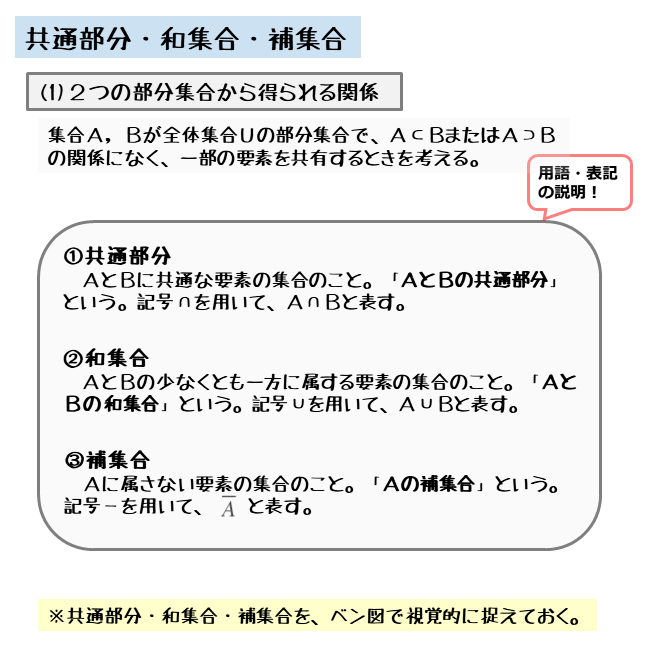
共通部分・和集合・補集合
集合には、全体集合、部分集合、空集合などいくつかの種類がありました。今回は、2つの集合が包含関係のある場合ではなく、たとえば2つの集合が一部だけ重なるような場合を扱います。
そのような関係にある集合では、共通部分・和集合・補集合といった集合を扱います。
今後は、包含関係にある集合だけでなく、部分的に重なる集合についても扱います。出題頻度が高い単元なので、演習をこなしてしっかりマスターしましょう。
2つの集合の共通部分
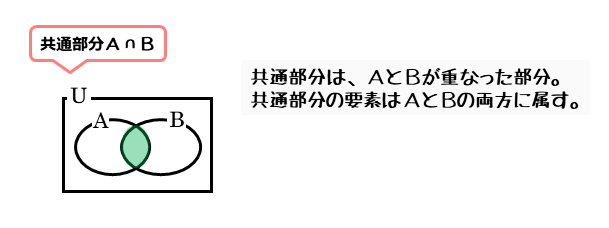
全体集合をUとし、またその部分集合をA,Bとします。この部分集合A,Bに共通な要素があるとき、その集まりを共通部分と言います。
共通部分は集合の1つですが「~集合」と言わないので注意しましょう。部分集合A,Bの共通部分は、記号∩を用いて「A∩B」と表されます。
部分集合A,Bの共通部分
部分集合 $A \ , \ B$ の共通部分は
\begin{align*} \quad A \cap B \end{align*}また、部分集合A,Bの共通部分A∩Bは、ベン図にすると部分集合A,Bが重なった部分になります。
共通部分も集合の1つなので、共通の要素が分かったら集合の表し方に則って表します。
共通部分の表し方の例
\begin{align*} &\quad A=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \} \\[ 5pt ] &\quad B=\{2 \ , \ 4 \ , \ 6 \ , \ 8 \} \end{align*}であるとき、共通部分 $A \cap B$ は
\begin{align*} \quad A \cap B =\{ 2 \ , \ 4 \} \end{align*}2つの集合の和集合
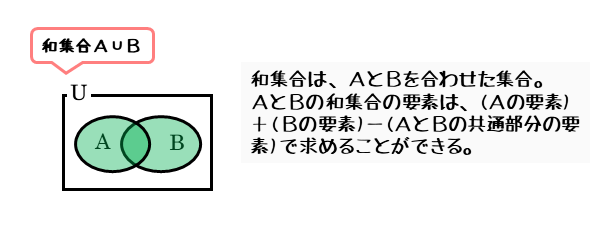
全体集合をUとし、その部分集合をA,Bとします。和集合とは、部分集合A,Bの少なくとも一方に属する要素の集合のことです。
「少なくとも一方」とあるので、両方の集合に同時に属する必要はありません。部分集合A,Bの和集合は、記号∪を用いて「A∪B」と表されます。
部分集合A,Bの和集合
部分集合 $A \ , \ B$ の和集合は
\begin{align*} \quad A \cup B \end{align*}また、部分集合A,Bの和集合A∪Bは、ベン図にすると部分集合A,Bを合わせた部分になります。
和集合A∪Bの要素は、単純に2つの部分集合A,Bの要素を合わせたものではありません。2つの部分集合A,Bが重なっているときは注意が必要です。このことはベン図を見ると良く分かります。
部分集合A,Bの重なる部分が共通部分A∩Bです。単純に部分集合A,Bの要素を合わせてしまうと、共通部分A∩Bのぶんだけ要素が重なってしまいます。二重になった共通部分A∩Bを取り除く必要があります。
共通部分と和集合の関係
共通部分と和集合の関係は
\begin{align*} \quad A \cup B = A + B \ – \left( A \cap B \right) \end{align*}共通部分と和集合の関係は、集合に属している要素の個数を数える問題ではよく利用されます。
和集合も集合の1つなので、要素が分かったら集合の表し方に則って表します。
和集合の表し方の例
\begin{align*} &\quad A=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \} \\[ 5pt ] &\quad B=\{2 \ , \ 4 \ , \ 6 \ , \ 8 \} \end{align*}であるとき、共通部分 $A \cap B$ は
\begin{align*} \quad A \cap B=\{2 \ , \ 4 \} \end{align*}であるので、和集合 $A \cup B$ は
\begin{align*} \quad A \cup B &= A + B \ – \left( A \cap B \right) \\[ 5pt ] &= \{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}+\{2 \ , \ 4 \ , \ 6 \ , \ 8 \}-\{2 \ , \ 4 \} \\[ 5pt ] &= \{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 8 \} \\[ 5pt ] \therefore \ A \cup B &= \{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 8 \} \end{align*}部分集合の補集合
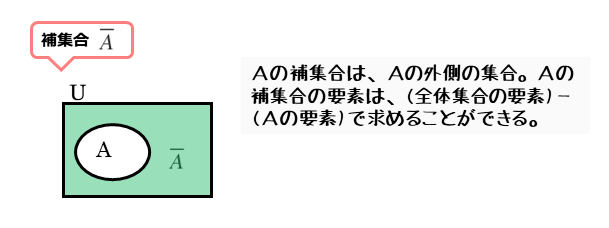
部分集合Aの補集合とは、部分集合Aに属さない要素の集合のことです。全体集合Uが定義されていれば、補集合に属する要素の個数は有限個です。
この補集合を上手に利用すると、共通部分や和集合を簡単に求めることもできます。補集合は、もとの集合のアルファベットの上に横線(  ̄ )をのせて表記します。
部分集合Aの補集合
部分集合 $A$ の補集合は
\begin{align*} \quad \overline{A} \end{align*}また、部分集合Aの補集合は、ベン図にすると部分集合Aの外側の部分になります。
部分集合Aの補集合の要素は、全体集合Uから部分集合Aを取り除いた後の残りの要素になります。この補集合を利用すれば、全体集合Uの要素から部分集合Aの要素を求めることもできます。
全体集合と補集合の関係
全体集合と補集合の関係は
\begin{align*} \quad \overline{A} = U \ – A \end{align*}補集合も集合の1つなので、属する要素が分かったら集合の表し方に則って表します。
補集合の表し方の例
\begin{align*} &\quad U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 5 \} \\[ 5pt ] &\quad A=\{2 \ , \ 4 \} \end{align*}であるとき、補集合 $\overline{A}$ は
\begin{align*} \quad \overline{A} &= U \ – A \\[ 7pt ] &= \{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 5 \} -\{2 \ , \ 4 \} \\[ 7pt ] &= \{ 1 \ , \ 3 \ , \ 5 \} \\[ 7pt ] \therefore \ \overline{A} &= \{ 1 \ , \ 3 \ , \ 5 \} \end{align*}補集合を利用する考え方は、逆側からの視点での考え方になります。1つの事柄を複数の視点から捉えようとすることは、問題を解く上でとても大切です。
正攻法で上手くいきそうにないとき、このような違った視点が持てると、思いのほか簡単に解ける場合もあるので意外と侮れません。
要点をまとめると以下のようになります。
ド・モルガンの法則は補集合の関係を表した式
補集合と言っても、色々な集合の補集合があります。たとえば、部分集合や共通部分などの補集合があります。色々な補集合の関係を式で表したものが「ド・モルガンの法則」です。
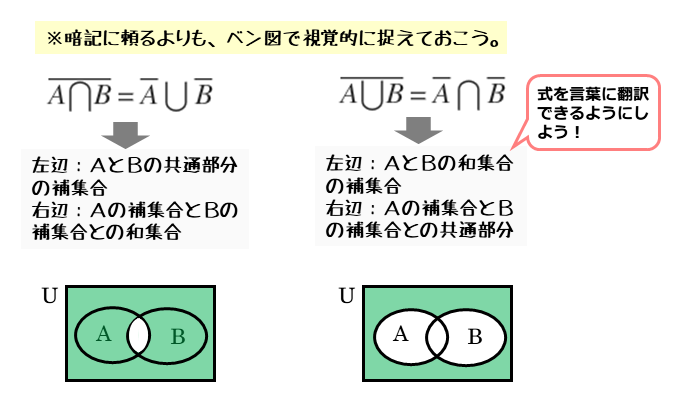
ド・モルガンの法則
\begin{align*} \quad \overline{A \cap B} &= \overline{A} \cup \overline{B} \\[ 7pt ] \overline{A \cup B} &= \overline{A} \cap \overline{B} \end{align*}ベン図を描いてみると、これらの式が成り立つことが分かります。
ド・モルガンの法則を機械的に利用する
問題では、部分集合の要素が与えられることがほとんどで、補集合の要素が与えられるのはまれです。ですから、基本的には補集合の要素を自分で求める必要があります。
もちろん、$\overline{A \cap B}$ や $\overline{A} \cup \overline{B}$ などの要素であっても、自力で求めることは可能です。しかし、扱う要素の個数が多くなると面倒になります。
そのときに有効なのが「ド・モルガンの法則」です。入試でも頻出なので使いこなせるようにしておきたいところです。そうなると覚える必要があるわけですが、形が似ているので間違えそうです。
しかし、いくつかのポイントを押さえると、簡単にそして機械的に扱うことができるようになります。「機械的に扱える」ことが利点です。
ド・モルガンの法則
\begin{align*} \quad \overline{A \cap B} &= \overline{A} \cup \overline{B} \\[ 7pt ] \overline{A \cup B} &= \overline{A} \cap \overline{B} \end{align*}2つの式を観察してみると、以下のようなことが分かります。
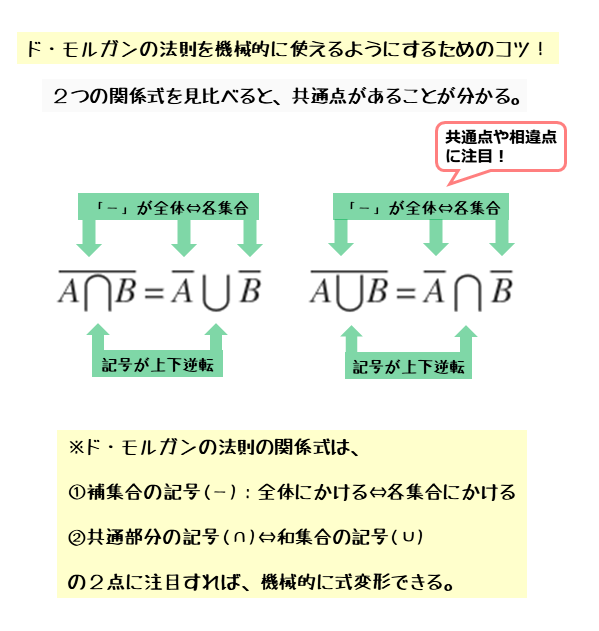
ド・モルガンの法則の式から分かること
- 左辺と右辺で、共通部分の記号∩と和集合を表す記号∪が入れ替わる
- 左辺と右辺で、全体にかかる補集合の記号̚̚ ̄と各集合にかかる補集合の記号 ̄が入れ替わる
ここでの全体とは、左辺や右辺の全体という意味で、共通部分や和集合のことを指します。この2つのことに気づけば、理屈が分からなくても、機械的に扱うことができるようになります。
ド・モルガンの法則を使った式の変形
補集合の記号「 $\bar{}$ 」:(全体なら各集合へ)⇔(各集合なら全体へ)
共通部分や和集合の記号「⋂,⋃」:(⋂なら⋃へ)⇔(⋃なら⋂へ)
図解すると以下のようになります。
補集合を扱った式が出てきたとき、2つのポイントを踏まえて変形してみましょう。変形後の方が明らかに要素を求めやすい場合があります。
次は、共通部分や和集合を扱った問題を実際に解いてみましょう。