数と式|整式をたすき掛けで因数分解してみよう

今回は、「たすき掛け」による因数分解を学習しましょう。
計算問題なので、演習をこなしながら学習すると効率が良いでしょう。もし、因数分解の基本的な方針や流れがまだ中途半端であれば、前の単元も確認しておきましょう。
「たすき掛け」による因数分解は、単なる計算問題だけでなく、色々な問題の中で利用されます。たとえば、「2次関数」では、点の座標を求めるときに利用することがあります。
「数と式」は、数や式についての基本的な扱い方を学習する単元です。徹底的に演習しておき、安心して数式を扱えるようにしておきましょう。それが今後の数学ライフをより良く送れるかどうかにつながります。
たすき掛けによる因数分解のおさらい
「たすき掛け」はどんな形の式で利用できたか覚えているでしょうか。以下のような条件を満たす整式に対して利用できます。
たすき掛けを利用できる整式の条件
- 特定の文字(たとえばx)についての2次式であること。
- 2次の項、1次の項、定数項の3つの項があること。
数式を扱うときには、式を見て方針が立つようになることを目標にしましょう。
典型的で頻出の問題を解いて、たすき掛けをマスターしよう
ここで紹介する問題は、たすき掛けを利用するものの中でも典型的で頻出の問題です。たすき掛けの使い所を押さえて、因数分解の流れを把握しましょう。
また、展開と因数分解の関係だけでなく、特定の文字に着目するなど、整式についての知識も問われています。これまで学習した内容を凝縮したような問題なので良問です。
扱う文字の種類や項数が多くなっても慌てずに。入試レベルならもっと複雑な整式を扱う。演習をこなして慣れていこう。
たすき掛けを利用して整式を因数分解してみよう
次の整式を因数分解してみましょう。
問
次の整式を因数分解しなさい。
\begin{align*} &1. \quad x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] &2. \quad x^2 +xy-2y^2 +x+5y-2 \end{align*}与式を観察すると、以下のようなことが分かります。
与式から分かること
- 文字がx,yの2種類ある。
- 文字x,yについて、ともに2次の項、1次の項、定数項の3項がある。
文字x,yを含む整式で、ともに2次の項があれば、ほぼたすき掛けで因数分解できます。
問1の解答・解説
問1
次の整式を因数分解しなさい。
\begin{align*} \quad x^2 +3xy+2y^2 -2x-3y+1 \end{align*}特定の文字に着目して整式を整理する
与式には2種類の文字x,yがあります。与式を扱いやすくするために、xに着目して降べきの順に整理します。
このとき、同類項に注意して整理します。
問1の解答例 1⃣
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(2y^2 -3y+1 \right) \end{align*}xに着目したので、yは数と同じ扱いをします。このとき、1次の項や定数項に注意が必要です。
着目する文字があると記述が変わる
着目する文字がなければ
\begin{align*} \quad x\left(3y-2 \right) \end{align*}⇒ 項の中ではカッコは一番後ろが基本
$x$ に着目すると
\begin{align*} \quad \left(3y-2 \right)x \end{align*}⇒ 係数が分かるように $x$ は一番後ろ
また、定数項は多項式になるので、カッコでくくっておきます。定数項の範囲が分かるようにするためです。定数項はyについての2次式になっています。
特定の文字に着目して整式を整理すると、整式の見え方が変わる。扱い方の方針が立たないときは、次数の高い、または次数の低い文字に着目して整式を整理してみよう。
定数項が和の形だと因数分解できない
xに着目して与式を整理できたので、因数分解したいところですが、もう少し与式を変形する必要があります。
ここで、xについての1次式どうしの展開(乗法公式4番目)を思い出してみましょう。
xについての1次式どうしの展開(乗法公式4番目)
\begin{align*} &\left(ax+b \right)\left(cx+d \right) \\[ 7pt ] = \ &acx^2 +\left(ad+bc \right)x+bd \end{align*}公式の定数項は、因数b,dの積で表されています。それに対して、与式の定数項は、多項式なので和の形で表されています。このままでは定数項の因数が分からないので、因数分解できません。
定数項の因数を知るために、yについての2次式を因数分解して積の形にします。ここで利用するのがたすき掛けです。
定数項だけで見れば、yについて、2次の項、1次の項、定数項を持つ多項式です。2次の項の係数が1ではないので、たすき掛けで因数分解します。
たすき掛けを利用して、与式の定数項を因数分解します。
問1の解答例 2⃣
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(2y^2 -3y+1 \right) \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(y-1 \right)\left(2y-1 \right) \end{align*}これで定数項を積の形で表せました。
定数項だけで因数分解する方法は、たすき掛けとは限らない。共通因数でくくったり、他の乗法公式を利用したりする場合もある。
因数の組み合わせは符号に気を付けよう
定数項を因数分解すると、yの1次式どうしの積の形になるので、これらが因数の候補になります。
因数の候補としたのは、符号のことを考慮していないからです。定数項の因数分解に注意が向きすぎて、符号のことを忘れがちになります。
因数分解後の定数項から分かる因数の組み合わせは、次の2通り考えられます。
定数項の因数の組み合わせ
定数項は因数分解すると
\begin{align*} \quad +\left(y-1 \right)\left(2y-1 \right) \end{align*}より、因数の組み合わせは
\begin{align*} &\quad +\left(y-1 \right) \ , \ +\left(2y-1 \right) \\[ 7pt ] &\quad -\left(y -1 \right) \ , \ -\left(2y-1 \right) \\[ 7pt ] \end{align*}の $2$ 通り考えられる。
正負の数の乗除算で、符号の規則性を学習したことを思い出しましょう。また、yについての1次式を1つの文字に見立てると、符号の組み合わせを考えやすくなります。
式全体のたすき掛けでは、yの係数に注目
定数項の因数が分かったら、次は式全体をたすき掛けで因数分解します。
xの2次の項の係数を見て、因数の組み合わせを考えます。係数は1なので、因数は1,1の組み合わせです。
分かった因数を上下に並べます。
問1の解答例 3⃣
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(2y^2 -3y+1 \right) \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(y-1 \right)\left(2y-1 \right) \end{align*}$x$ について $2$ 次の項の係数に注目して
\begin{align*} \begin{array}{ccc} 1 & & \\ 1 & & \\ \hline \end{array} \end{align*}次に、定数項の因数を上下に並べます。因数の候補が2通りあったので、並べ方に迷いますが、yの係数を参考にして候補を絞ります。
yの係数を参考にする
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(\underline{3y}-2 \right)x+\left(\underline{y}-1 \right)\left(\underline{2y}-1 \right) \end{align*}特に、$x$ について $1$ 次の項をよく見よう。
xの1次の項では、yの係数は+3です。+3であることに注意すると、定数項の因数は+(y-1)と+(2y-1)になると予想できます。負の数の組み合わせであれば、+3yになりません。
定数項の因数を上下に並べます。実際にたすき掛けして、xの1次の項の係数+(3y-2)に等しくなることを確かめます。
問1の解答例 4⃣
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(2y^2 -3y+1 \right) \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(y-1 \right)\left(2y-1 \right) \end{align*}$x$ について $2$ 次の項の係数に注目して
\begin{align*} \begin{array}{ccc} 1 & & \\ 1 & & \\ \hline \end{array} \end{align*}$x$ について定数項の因数から
\begin{align*} \begin{array}{ccccc} 1 & \searrow & \left( y -1 \right) & \longrightarrow & y-1 \\ 1 & \nearrow & \left( 2y -1 \right) & \longrightarrow & 2y-1 \\ \hline 1 & & \left( y -1 \right) \left( 2y -1 \right) & & \underline{\underline{3y-2}} \end{array} \end{align*}定数項の因数は多項式ですが、yの項だけに注目すると、符号や数字の組み合わせを考えやすくなります。
たすき掛けが上手くいけば、因数分解の続きに追記して終了です。
問1の解答例 5⃣
\begin{align*} \quad &x^2 +3xy+2y^2 -2x-3y+1 \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(2y^2 -3y+1 \right) \\[ 7pt ] = \ &x^2 +\left(3y-2 \right)x +\left(y-1 \right)\left(2y-1 \right) \\[ 7pt ] = \ &\left\{x+\left(y-1 \right) \right\}\left\{x+\left(2y-1 \right) \right\} \quad \cdots \text{①} \\[ 7pt ] = \ &\left(x+y-1 \right)\left(x+2y-1 \right) \quad \cdots \text{②} \end{align*}たすき掛けの結果が出てから①,②を追記する。
\begin{align*} \begin{array}{ccccc} 1 & \searrow & \left(y-1 \right) & \longrightarrow & y-1 \\ 1 & \nearrow & \left(2y-1 \right) & \longrightarrow & 2y-1 \\ \hline 1 & & \left(y-1 \right) \left(2y-1 \right) & & \underline{\underline{3y-2}} \end{array} \end{align*}$x$ の $1$ 次の項の係数に等しくなったので終了。
問1のポイントと解答例をまとめると以下のようになります。
問2の解答・解説
問2
次の整式を因数分解しなさい。
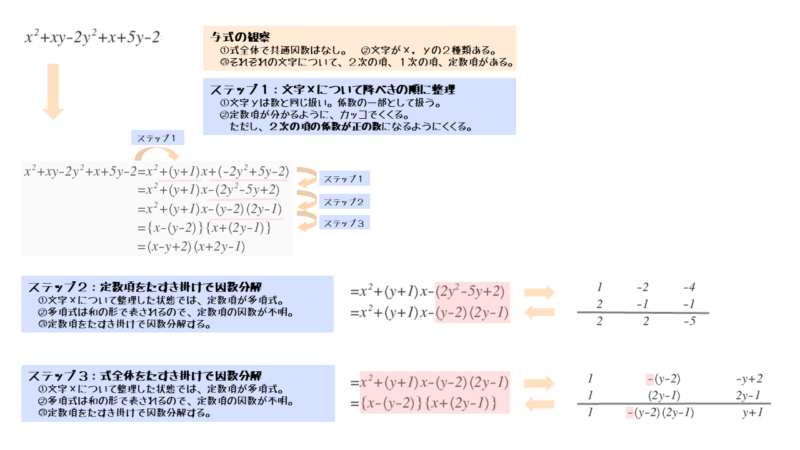
\begin{align*} \quad x^2 +xy-2y^2 +x+5y-2 \end{align*}2次の項の係数は正の数にしておこう
与式をxについて降べきの順に整理します。このとき注意したいのは、定数項をカッコでくくるときです。
2次式を因数分解をするとき、2次の項の係数が正の数である方が、符号の組み合わせや乗法公式の利用などを考えると扱いやすいです。
問2も問1と同じように、定数項を因数分解する必要があります。yの2次の項の係数が正の数になるように、カッコでくくります。
問2の解答例 1⃣
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x \underline{\underline{-\left(2y^2 -5y+2 \right)}} \end{align*}最高次の項(2次の項)の係数を正の数にするのは基本作業と思っておこう。2次関数の平方完成でも似たようなことをするので覚えておこう。
定数項を因数分解して、因数の組み合わせを考える
次に、定数項をたすき掛けで因数分解します。
問2の解答例 2⃣
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(2y^2 -5y+2 \right) \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(y-2 \right)\left(2y-1 \right) \end{align*}定数項を因数分解できたら、因数の組み合わせを考えます。このとき符号に注意しましょう。
因数分解後の定数項から分かる因数の組み合わせは、次の2通り考えられます。
定数項の因数の組み合わせ
定数項は因数分解すると
\begin{align*} \quad -\left(y-2 \right)\left(2y-1 \right) \end{align*}より、因数の組み合わせは
\begin{align*} &\quad -\left(y-2 \right) \ , \ +\left(2y-1 \right) \\[ 7pt ] &\quad +\left(y-2 \right) \ , \ -\left(2y-1 \right) \end{align*}の $2$ 通り考えられる。
因数の候補が分かったので、たすき掛けを利用して式全体を因数分解します。
xの2次の項の係数を見て、因数の組み合わせを考えます。係数は1なので、因数は1,1の組み合わせです。
分かった因数を上下に並べます。
問2の解答例 3⃣
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(2y^2 -5y+2 \right) \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(y-2 \right)\left(2y-1 \right) \end{align*}$x$ について $2$ 次の項の係数に注目して
\begin{align*} \begin{array}{ccc} 1 & & \\ 1 & & \\ \hline \end{array} \end{align*}yの係数に注目して、定数項の因数の組み合わせを予想しておきます。
yの係数を参考にする
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(\underline{y}+1 \right)x-\left(\underline{y}-2 \right)\left(\underline{2y}-1 \right) \end{align*}特に、$x$ について $1$ 次の項をよく見よう。
xの1次の項では、yの係数は+1です。+1であることに注意すると、定数項の因数は-(y-1)と+(2y-1)になると予想できます。異符号の組み合わせなので注意しましょう。
定数項の因数を上下に並べます。実際にたすき掛けして、xの1次の項の係数+(y+1)に等しくなることを確かめます。
問2の解答例 4⃣
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(2y^2 -5y+2 \right) \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(y-2 \right)\left(2y-1 \right) \end{align*}$x$ について $2$ 次の項の係数に注目して
\begin{align*} \begin{array}{ccc} 1 & & \\ 1 & & \\ \hline \end{array} \end{align*}$x$ について定数項の因数から
\begin{align*} \begin{array}{ccccc} 1 & \searrow & -\left(y-2 \right) & \longrightarrow & -y+2 \\ 1 & \nearrow & \left(2y-1 \right) & \longrightarrow & 2y-1 \\ \hline 1 & & -\left(y-2 \right)\left(2y-1 \right) & & \underline{\underline{y+1}} \end{array} \end{align*}たすき掛けが上手くいけば、因数分解の続きに追記して終了です。
問2の解答例 5⃣
\begin{align*} \quad &x^2 +xy-2y^2 +x+5y-2 \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(2y^2 -5y+2 \right) \\[ 7pt ] = \ &x^2 +\left(y+1 \right)x-\left(y-2 \right)\left(2y-1 \right) \\[ 7pt ] = \ &\left\{x-\left(y-2 \right) \right\}\left\{x+\left(2y-1 \right) \right\} \quad \cdots \text{①} \\[ 7pt ] = \ &\left(x-y+2 \right)\left(x+2y-1 \right) \quad \cdots \text{②} \end{align*}たすき掛けの結果が出てから①,②を追記する。
\begin{align*} \begin{array}{ccccc} 1 & \searrow & -\left(y-2 \right) & \longrightarrow & -y+2 \\ 1 & \nearrow & \left(2y-1 \right) & \longrightarrow & 2y-1 \\ \hline 1 & & -\left(y-2 \right)\left(2y-1 \right) & & \underline{\underline{y+1}} \end{array} \end{align*}$x$ の $1$ 次の項の係数に等しくなったので終了。
問2のポイントと解答例をまとめると以下のようになります。
たすき掛けによる因数分解を2セット行う
ここで扱った因数分解の問題では、因数を考えるために定数項を因数分解する必要があります。そのため、定数項と式全体とでたすき掛けを2セット行っていることになります。
たすき掛けを2セット行う因数分解の流れをまとめると以下のようになります。
たすき掛けを2セット行う因数分解の流れ
- 文字xについて、整式を降べきの順に整理する。
- 定数項だけをたすき掛けで因数分解して、因数を求める。
- 定数項の因数が分かったら、式全体をたすき掛けで因数分解する。
たすき掛けを扱った因数分解では頻出の問題です。2種類の文字(たとえばx,y)を含む2次式の因数分解であれば、まずこの解き方を検討してみましょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 2種類の文字x,yがあり、それらの2次の項があったら、たすき掛けによる因数分解2セットを候補に。
- 文字xに注目して、整式を降べきの順に整理する。
- 注目しない文字yは数と同じ扱いをする。
- 定数項をカッコでくくるとき、2次の項の係数は正の数になるようにする。
- 定数項では、文字yに着目して2次式を因数分解して積の形にする。
- たすき掛けによる因数分解では、符号と数字の正しい組み合わせを探せばよい。