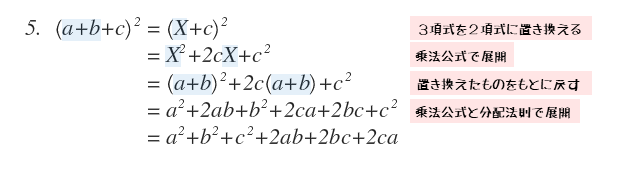数と式|整式の展開と乗法公式について

今回は整式の展開と乗法公式についてです。
展開の意味や分配法則との関係、そして乗法公式がどのようにして得られたのかが分かれば演習をこなしましょう。
展開の意味と分配法則との関係
展開の定義
展開とは、積の形で表された式を、和の形で表すことです。式を見るとカッコがなくなるので、展開のことを「カッコをはずす」と教わる場合もあります。
その後に学習する因数分解とはちょうど逆の操作になります。ですから、展開と因数分解は合わせて学習すると効率的です。
定義にあるように、もとの式は全体で積の形なので単項式ですが、展開すると和の形になるので多項式になります。つまり乗算から加算に変換しているのが式の展開だと言えます。
外見から判断するなら、カッコの有無や、くっついた数や文字で。計算上は乗算から加算への変換が式の展開。
式の展開は分配法則を利用したもの
乗算から加算への変換で思いつくのが、分配法則です。分配法則は、文字式に限らず、数の計算でも利用される法則です。
中学での分配法則は、主に単項式と多項式の積から1つの多項式に書き換えるときに使われます。それに対して、高校での分配法則は、主に多項式どうしの積から1つの多項式にするときに使われます。
多項式どうしでの分配法則では、片方の多項式を1つの文字に置き換えて単項式にするのがポイントです。
置き換え後は、中学での分配法則の形になり、式を展開できます。展開した後は、置き換えた文字を元の多項式に戻すと、また中学での分配法則の形になるので同じようにして式を展開します。
このように導出の過程を見ていくと、既習内容との関わりを知ることができ、覚えた事柄の使い所も分かります。これが公式の導出を勧める理由です。
多項式どうしの展開では、分配法則を2セット行えば良い。分配法則は既に覚えているので、あとは使い方だけ。
乗法公式は計算過程を省略するための式
分配法則を用いると、多項式どうしの積を展開することができました。しかし何度も分配法則を2セット行うのは面倒です。
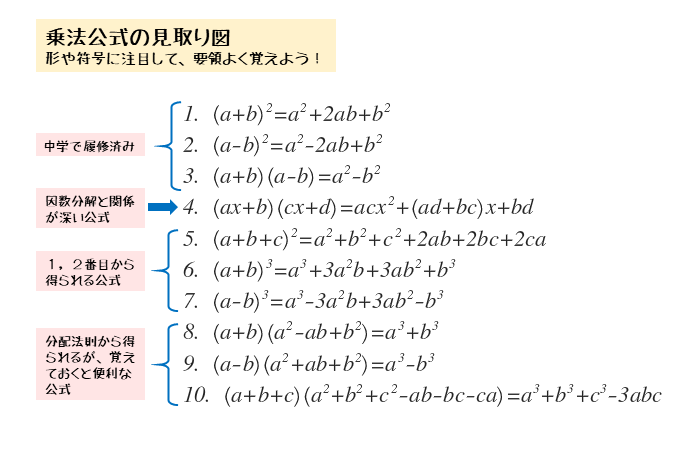
その面倒さを省くのが乗法公式です。この乗法公式は、頻繁に扱う多項式どうしの積が対象です。式の形や符号に注目すると、公式を覚えるのがだいぶ楽になります。
式の展開は分配法則を利用すればできるので、乗法公式なんて覚えなくても良いのでは?と思うかもしれません。しかし、式によっては展開するのにだいぶ時間が掛かります。
乗法公式は計算過程を省略して結果を得ることができます。計算のミスやスピードを考えたとき、覚えておく方が絶対に良いでしょう。それに、覚えておかないと、式の因数分解で苦労することになります。
中学で履修済みの乗法公式
1~3番目の式は中学で履修済みの乗法公式です。
1番目の式は累乗の形で表されているので、分配法則を利用しやすい積の形に変形します。
2番目の式は、1番目と同様に分配法則を利用しても良いですが、1番目の式でbから-bに置き換えたと考えると、1番目の式の結果を利用して展開できます。
符号の違いや形の類似性に注目して覚えましょう。
3番目の乗法公式も中学でも学習しています。ただし、高校ではbの部分が文字を含む項になっていることが多くなります。
この式の計算過程を見るとよく分かりますが、分配法則で展開すると同類項が出てくるので、それを整理する必要があります。しかも同類項は相殺されます。
分配法則による展開だと、相殺されて消えてしまう項を展開のたびに書く必要がありますが、乗法公式だとその手間を省けます。
たすき掛けに関わる乗法公式
4番目以降から本格的に高校で学習する公式です。
xについての1次式どうしの積です。展開後はxについての2次式で、降べきの順に並んだ式になっています。
分配法則で展開すると、2,3番目の項が同類項なので整理する必要があります。分配法則すると4項からなる多項式でしたが、最終的には3項からなる多項式になります。
ポイントになるのはxの1次の項です。係数を見ると、展開前の内側2項の積と外側の2項の積との和になっています。
4番目の乗法公式は、因数分解で学習するたすき掛けに関わる。展開するときにカッコ内の項がそれぞれどの項と関わるのかを知っておこう。
これまでの乗法公式が使えるように工夫した公式
5番目の乗法公式
5番目の乗法公式は、3項からなる多項式を2乗した式です。
これまではカッコ内の項は2項でした。3項からなる多項式でも分配法則を3セット行えば展開できますが、手間が掛かります。
そこで項の数を減らす工夫をします。2つの項の和を1つの文字に置き換えて、2項からなる多項式にします。3項式から2項式に置き換える工夫のおかげで、1番目の乗法公式で展開できるようになります。
この式の展開の仕組みが分かったら、一気に展開できるように覚えましょう。
6,7番目の乗法公式
6,7番目の乗法公式は3乗公式と呼ばれることもある公式です。符号の違いだけで形が似ているので、セットで覚えましょう。
2項式を3乗するので、工夫して展開します。指数法則を利用すると、指数を1と2に分けることができます。
1番目の乗法公式を利用できる形に変形できました。展開後、さらに分配法則で展開します。同類項が出てくるので整理します。
7番目の式は、6番目の式でbから-bに置き換えたと考えると、6番目の式を利用して展開できます。6番目の最後の式でbから-bに置き換えて整理すると得られます。
8~10番目の乗法公式
8~10番目の乗法公式は割愛しますが、分配法則で展開し、同類項を整理すると得られます。特に10番目の式は、応用問題以外ではほとんど見かけないかもしれません。
乗法公式を覚える優先順位は、以下を参考にしましょう。
乗法公式を覚えるときの目標レベル
- 1~5番目の乗法公式 … 九九と同じレベルで扱えるようにしておく。(最優先)
- 6~9番目の乗法公式 … 覚えていなくても展開しようと思えばできるレベルに。
- 10番目の乗法公式 … 証明問題で利用することがあるので、余裕があれば覚えておく。
6番目以降の公式は数学2で学習するので、数学1や数学Aの範囲では覚えなくても問題ないでしょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 式の展開は多項式の積を1つの多項式で表すこと。
- 式の展開は、分配法則を利用して行う。
- 特定の多項式の積であれば、乗法公式で展開できる。
- 乗法公式は、共通点や相違点に注目して要領よく覚えよう。
- 式を見て、乗法公式に当てはまるかの判断がつくまで演習しよう。
- xの1次式どうしの積は、因数分解のたすき掛けに深く関わるので、仕組みをよく理解しておく。