2次関数|2次関数の平方完成について

2次関数の式は、中学で学習した2乗に比例する関数を平行移動した式だということを前回の記事で学習しました。
また、2次関数の標準形と呼ばれる式であれば、軸・頂点・凸の情報を知ることができます。これらの情報をもとにグラフを簡単に描くことができます。
しかし、いつも与式が標準形であるとは限りません。そのようなとき、自分で式を標準形に変形する必要があります。
今回は、2次関数の式を標準形に変形する「平方完成」という方法を学習します。
2次関数の式を標準形で表す習慣を
2次関数では、式が標準形で表されていれば、そのグラフを描くことができます。軸の方程式・頂点の座標・上または下に凸の3つの情報を得ることができるからです。
ですから、2次関数を扱う場合、特に断りがなくても、つねに式を標準形で表すことが大切です。
実際の問題では、与式が標準形でない場合がほとんど。標準形に変形できるかどうかも出題の意図に含まれているからだろう。
2次関数の基本作業と言っても良い「標準形への変形」で躓かないように、式変形の手順をしっかりとマスターしましょう。
標準形への変形は平方完成がポイント
2次関数の式を思い出してみましょう。2乗に比例する関数を平行移動した後の式を思い出せれば良いでしょう。
ここで注意したいのは、2次関数の式は変数xの2次式であればよいので、式の表し方には2パターンあるということです。
2次関数の式は2パターン
\begin{align*} \quad a \neq 0 \end{align*}とする。このとき、$2$ 次関数の式は
\begin{align*} &\quad y = ax^2 +bx +c \quad \cdots \text{①} \\[ 7pt ] &\quad y = a \left(x-p \right)^2 +q \quad \cdots \text{②} \end{align*}の$2$ 通りで表せる。
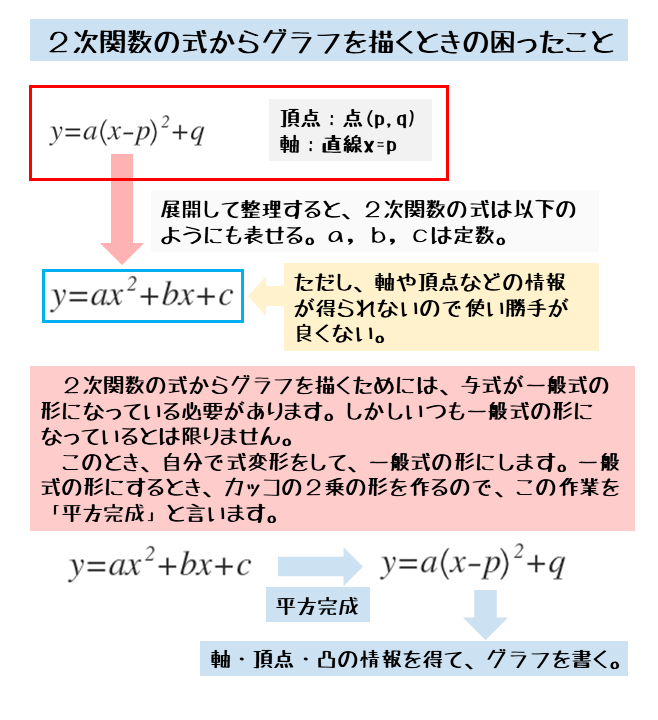
①式は一般的な2次式で、②式は標準形と言われる式です。標準形の②式を展開し、各項の係数や定数項をa,b,cに置き換えると①式が得られます。
一般に、設問では与式が一般的な2次式(①式)で与えられることがほとんどです。
一般的な2次式の弱点は、軸・頂点・凸の情報を得ることができないことです。この式のままだと、グラフを描くことができません。ですから軸・頂点・凸の情報を得るために、標準形の式に変形する必要があります。
一般的な2次式ではグラフを描くときに苦労する。2次関数では標準形を使うことが多い。
2つの2次関数の式を見比べると、標準形の式は、a(x-p)2の項をもつことから、一般的な2次式を部分的に因数分解した式だと考えることができます。
一般的な2次式からa(x-p)2の形を作ることを「平方完成」と言います。与式を自力で標準形の式に変形することで、グラフを描くのに必要な情報を得ることができるようになります。
2乗のことを平方と言うことがある。面積の単位などがそれにあたる。
2つの式の関係についてまとめると以下のようになります。
平方完成の考え方
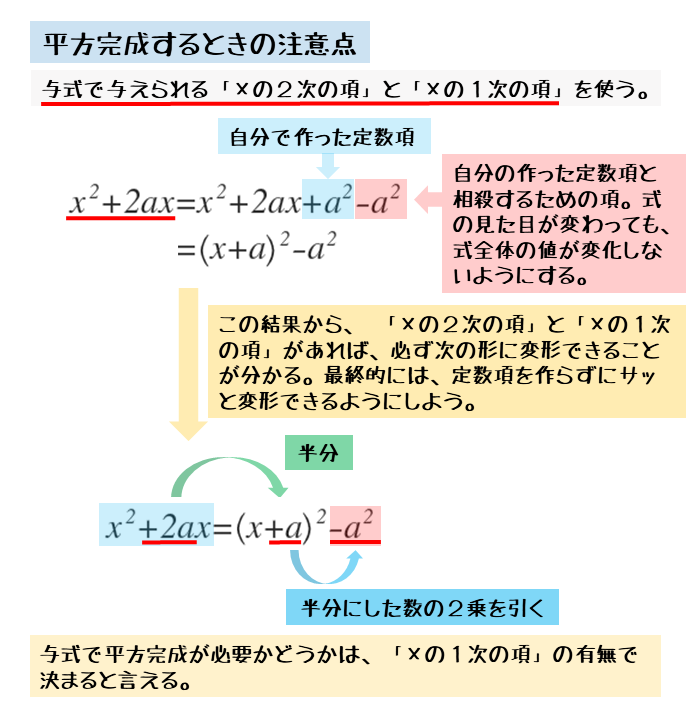
平方完成が必要な式には、変数xについて、2次の項ax2と1次の項+bxが存在します。この2つの項から乗法公式を利用してa(x-p)2の形を作ります。
平方完成に利用する項は2次と1次の項。定数項は利用しない。
利用する乗法公式はこちらです。
平方完成に利用する乗法公式
\begin{align*} \quad x^2 +2ax+a^2 = \left(x+a \right)^2 \end{align*}具体例を挙げて考えてみましょう。たとえば、x2+6xを平方完成します。
このままでは乗法公式に当てはまりません。平方完成するためには、定数項が必要です。どんな定数項があれば良いかを考えてみましょう。
1次の項の係数との関係から、係数+6の半分である+3を2乗した数(+3)2が定数項にあれば、平方完成できます。
平方完成の仕組み
\begin{align*} \quad \left( x+3 \right)^2 =x^2 +2 \cdot 3x+3^2 \end{align*}であるので、$x^2 +6x$ には定数項 $3^2$があれば平方完成できる。
\begin{align*} \quad x^2 +6x+3^2 =\left( x+3 \right)^2 \end{align*}乗法公式における1次の項の係数と定数項との関係を知っていれば、定数項を作ることは難しくありません。演習をこなせば、簡単に平方完成できるようになります。
式変形するのは自由だが、式の値を変えないようにしよう
自分で定数項を作れば、2乗の形を作り出せます。ここで注意したいのが、作り出した定数項はもともと与式にはなかったということです。
もともとなかったものを書き加えたので、与式に何かしらの値を加算したことになります。加算したことで、式全体の値が変わってしまいます。
その不都合をなくすには、同じ値を引くことで相殺されるようにしなければなりません。この作業をしないと、もとの式に戻りません。
x2+6xを平方完成する
\begin{align*} \quad x^2 +6x &= x^2 +2 \cdot 3x \underline{+3^2 -3^2} \\[ 7pt ] &= \left(x+3 \right)^2 -3^2 \end{align*}単に定数項を加えるだけでなく、加えた定数項を引く処理が必要です(下線部分)。
イメージは分母の有理化に近い。値は変わらないが、式の見た目が変わる変形。
一般に、平方完成の式は次のように表せます。乗法公式を変形すると得られる式です。
平方完成の式
\begin{align*} \quad x^2 +2ax+a^2 = \left(x+a \right)^2 \end{align*}左辺の定数項を右辺に移項して
\begin{align*} \quad x^2 +2ax = \left(x+a \right)^2-a^2 \end{align*}与式にある2次の項と1次の項、そして自分で作った定数項の3つの項を用いて、2乗の形を作ります。これが平方完成の考え方や仕組みです。
平方完成するとき、定数項を作るために1次の項の係数を利用します。ですから、平方完成できるかどうかは1次の項の有無で決まると覚えておくと、式変形の方針を立てやすくなります。
また、平方完成は、上述のように乗法公式を変形する方法で解説されることもあります。自分が理解しやすい方法で仕組みを理解しましょう。ただし、自分で項を作り出す考え方は意外と利用されるので、知っておいた方が無難です。
次は平方完成を扱った問題を解いてみましょう。
平方完成を扱った問題を解いてみよう
次の2次関数の式をそれぞれ平方完成してみましょう。
問1,2の両方に定数項がありますが、無視して平方完成しましょう。2次の項と1次の項の2つの項と、自分で作った定数項を使って平方完成します。
問1の解答・解説
問1
次の式を平方完成せよ。
\begin{align*} \quad y=x^2+6x+5 \end{align*}1次の項の係数を参考にして定数項を作ります。係数の半分を2乗したものが定数項です。
式の値が変わらないように、作った定数項と同じ値を引きます。これでもとの式に戻ります。
問1の解答例
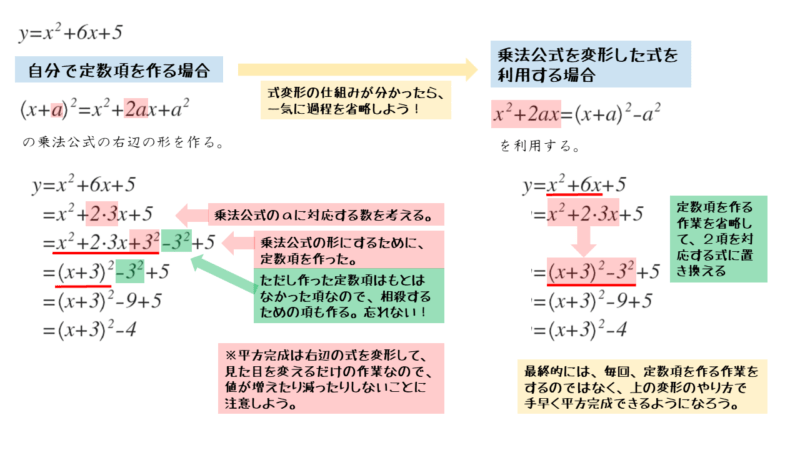
\begin{align*} \quad y &=x^2+6x+5 \\[ 7pt ] &=x^2+2 \cdot 3x \underline{+3^2-3^2}+5 \\[ 7pt ] &=\left(x+3 \right)^2-3^2+5 \\[ 7pt ] &=\left(x+3 \right)^2-9+5 \\[ 7pt ] &=\left(x+3 \right)^2-4 \end{align*}x2+6x+32で平方完成し、残りの定数項-32+5を整理すると、すべての作業は終了です。
慣れてくると、次のように変形することもできます。過程が異なるだけで同じ結果が得られます。
問1の別解例
\begin{align*} \quad y &=x^2+6x\underline{+5} \\[ 7pt ] &=x^2+6x\underline{+9-4} \\[ 7pt ] &=\left(x+3 \right)^2-4 \end{align*}別解例では、平方完成するための定数項が9だと分かれば、与式の定数項+5を+9-4と変形するだけで簡単に平方完成できるようになります。慣れてくると、別解例の方が素早く平方完成できるかもしれません。
問1のポイントと解答例をまとめると以下のようになります。
式変形に慣れてきたら、乗法公式を利用して一気に平方完成しよう。こちらの方が計算過程が少なく、素早く変形できる。
問2の解答・解説
問2
次の式を平方完成せよ。
\begin{align*} \quad y=x^2 -6x+8 \end{align*}問1と同じように、1次の項の係数を参考にして定数項を作ります。このとき、作った定数項と同じ値を引くことを忘れないようにしましょう。
問2の解答例
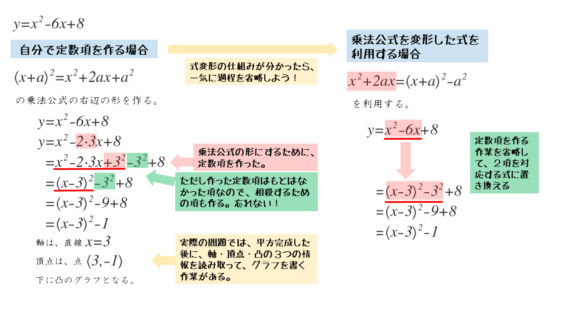
\begin{align*} \quad y &=x^2 -6x+8 \\[ 7pt ] &=x^2 +2 \cdot \left(-3 \right)x \underline{+\left(-3 \right)^2-\left(-3 \right)^2}+8 \\[ 7pt ] &=\left(x-3 \right)^2-\left(-3 \right)^2+8 \\[ 7pt ] &=\left(x-3 \right)^2-9+8 \\[ 7pt ] &=\left(x-3 \right)^2-1 \end{align*}x2-6x+(-3)2で平方完成し、残りの定数項-(-3)2+8を整理すると、すべての作業は終了です。
問1よりも注意したいのは、1次の項の係数が負の数であることです。実数の範囲では2乗すると必ず正の数になるので、大勢に影響はないかもしれませんが、負の数を扱うので慎重に取り組む習慣をつけましょう。
問2では、(x-a)2の乗法公式を利用したと考えれば、+32-32としても良い。
問2も同様に、次のように変形することもできます。過程が異なるだけで同じ結果が得られます。
問2の別解例
\begin{align*} \quad y &=x^2 -6x\underline{+8} \\[ 7pt ] &=x^2 -6x\underline{+9-1} \\[ 7pt ] &=\left(x-3 \right)^2-1 \end{align*}別解例では、平方完成するための定数項が9だと分かれば、与式の定数項+8を+9-1と変形するだけで簡単に平方完成できるようになります。
問2のポイントと解答例をまとめると以下のようになります。
どちらの問も易しい式変形なので、解くこと自体に問題はないでしょう。このような問題で必要なのは、流れや仕組みをしっかり把握することです。
Recommended books
関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。
関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。
関数は、たとえば物理の直線運動でもv-tグラフなどで登場するので、ぜひとも攻略しておきたい単元です。
オススメその1
1冊目に紹介するのは『おもしろいほどよくわかる高校数学 関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。
高校数学で学ぶ2次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。
書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。
オススメその2
2冊目に紹介するのは『改訂版 坂田アキラの2次関数が面白いほどわかる本』です。
『おもしろいほどよくわかる高校数学 関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。
高校数学の基幹分野である「2次関数」は坂田の解説でマスターせよ!
累計50万部超の「坂田理系シリーズ」の「2次関数」。2009年4月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「2次関数」対策の決定版!! 旧版になかった「解の配置」のテーマを増設。
教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。
オススメその3
2次関数は、高校数学で学習する関数の中で最も基本的なものです。ですから、苦手意識をもたないようにしっかりと取り組んでおいた方が良いでしょう。
参考書や問題集を上手に利用しましょう。その他にも以下のような教材があります。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 2次関数では、式を標準形で表すのが基本。
- 2次関数の式が一般的な2次式で表される場合、自分で標準形に変形する。
- 標準形への変形は、平方完成で行う。
- 平方完成では、1次の項の係数を利用。