２次関数｜２次関数の最大値や最小値を扱った問題を解いてみよう
２次関数の最大値や最小値について学習したら、学習内容を忘れないうちに問題を解きましょう。
考え方や流れを大筋で掴めたらすぐに演習すると良いでしょう。実際に解いてみることで、理解の不十分な箇所が見えてきます。
記事の画像が見辛いときはクリックすると拡大できます。
２次関数の最大値や最小値を扱った問題では場合分けが必須
２次関数の式や定義域が未知数を含まなければ、最大値や最小値を求めることは難しくありませんが、入試レベルになると話が変わってきます。
たとえば、未知の定数ａを用いて、定義域がａ≦ｘ≦ａ＋１などと与えられることもあります。
このような場合、定数ａの値によって定義域の位置が変わってしまいます。ですから、定数ａの値について場合分けをしなければ、最大値や最小値を求めることはできません。
入試レベルでは、最大値や最小値を場合分けして求める問題が頻出。きちんと解けるようにしておこう。
場合分けが必要な問題のタイプには２通りあります。
場合分けが必要な問題
- 軸の方程式に未知の定数（ａなど）が含まれる場合
- 定義域に未知の定数が含まれる場合
１つ目は、軸の方程式が変わるので、定義域に対するグラフの軸の位置が変わります。２つ目は、定義域が変わるので、グラフに対する定義域の位置が変わります。
どちらの場合にも言えるのは、グラフと定義域との相対的な位置が定まらないということです。ですから、場合分けなしでは最大値や最小値をとる点が決まりません。
場合分けの不要な問題を解いてみよう
次の問題を解いてみましょう。
このような問題では、場合分けなしで最大値や最小値を求めることができます。式の係数や定義域に未知の定数が含まれていません。
問１の解答・解説
問１
次の $2$ 次関数の最大値、最小値を求めよ。
\begin{align*} \quad y = {x}^{2} -4x+3 \quad \left(-1 \leqq x \leqq 4 \right) \end{align*}２次関数が出てきたら、とにかく標準形への変形を優先しましょう。
与式を平方完成して、軸・頂点・凸の情報を確認します。
問１の解答例 1⃣
与式を変形して
\begin{align*} \quad y &= {x}^{2} -4x+3 \\[ 7pt ] &= {\left(x-2 \right)}^{2} -1 \end{align*}よって
頂点 … $( 2 \ , \ -1 )$
軸 … 直線 $x=2$
向き … 下に凸
定義域が与えられているので、定義域を意識しながらグラフを描きます。
作図すると、グラフ（軸）と定義域の位置関係がよく分かります。
下に凸のグラフであり、かつ軸が定義域に入っています。下に凸のグラフでは、軸が定義域内にあれば頂点のｙ座標が最小値です。
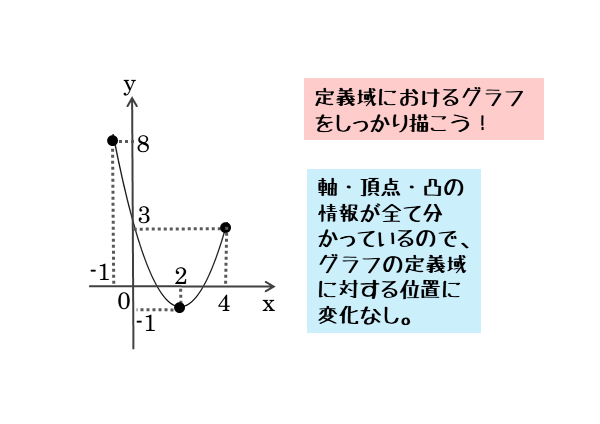
グラフに書き込んだｙ座標から２次関数の最小値を求めます。
問１の解答例 2⃣
グラフから $2$ 次関数の最小値は
$x=2$ のとき、最小値 $-1$
また、軸が定義域の右端寄りにあるので、定義域の左端に最大値をとる点ができます。
同様にして、グラフに書き込んだｙ座標から２次関数の最大値を求めます。
問１の解答例 3⃣
また、$2$ 次関数の最大値は
$x=-1$ のとき、最大値 $8$
２次関数の最大値・最小値の問題では、グラフの形状を上手に利用しよう。
問１のポイントと解答例をまとめると以下のようになります。
最大値や最小値をとる点は、頂点や定義域の両端の点のどれかになる。グラフをしっかり描こう。
問２の解答・解説
問２
次の $2$ 次関数の最大値、最小値を求めよ。
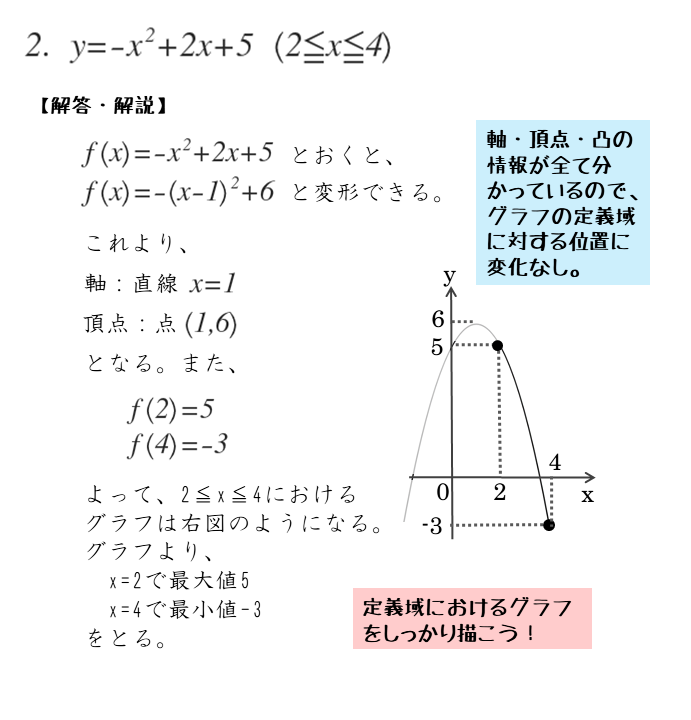
\begin{align*} \quad y=-{x}^{2} +2x+5 \quad \left(2 \leqq x \leqq 4 \right) \end{align*}与式を平方完成して、軸・頂点・凸の情報を確認します。
問２の解答例 1⃣
与式を変形して
\begin{align*} \quad y &= -{x}^{2} +2x +5 \\[ 7pt ] &= -\left({x}^{2}-2x \right) +5 \\[ 7pt ] &= -\left\{\left({x}-1 \right)^{2}-1 \right\} +5 \\[ 7pt ] &= -{\left(x-1 \right)}^{2} +6 \end{align*}よって
頂点 … $( 1 \ , \ 6 )$
軸 … 直線 $x=1$
向き … 上に凸
定義域が与えられているので、定義域を意識しながらグラフを描きます。
上に凸のグラフの場合、軸が定義域内にあれば頂点のｙ座標が最大値になります。
しかし、問２では軸が定義域に入っていません。
このような場合、上に凸のグラフであっても、頂点のｙ座標が最大値になることはありません。
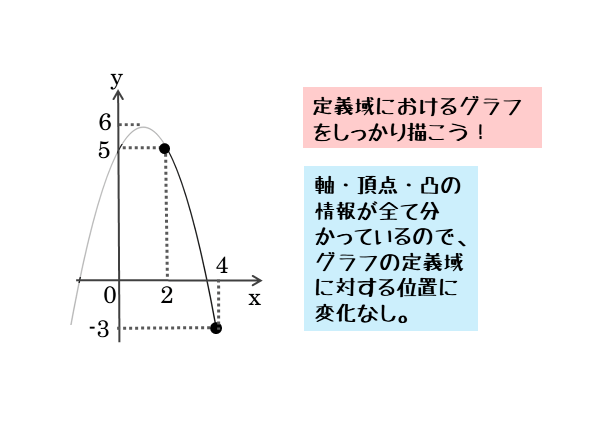
また、上に凸のグラフであり、かつ軸が定義域の左側にあります。つまり、グラフは軸よりも右側部分が定義域内にあります。
このような位置関係では、定義域の左端に最大値をとる点ができ、定義域の右端に最小値をとる点ができます。
グラフに書き込んだｙ座標から２次関数の最大値を求めます。
問２の解答例 2⃣
グラフから $2$ 次関数の最大値は
$x=2$ のとき、最小値 $5$
同様にして、グラフに書き込んだｙ座標から２次関数の最小値を求めます。
問２の解答例 3⃣
また、$2$ 次関数の最小値は
$x=4$ のとき、最小値 $-3$
問２のポイントと解答例をまとめると以下のようになります。
問１，２はともにグラフと定義域が定まるので、両者の位置関係が完全に決まってしまいます。両者の位置関係が固定されていれば、２次関数の最大値や最小値を求めることは難しくありません。
グラフ（軸）と定義域との位置関係によって、最大値や最大値をとる点が決まることが分かっています。実際に作図しながら確認すると、簡単に理解できるでしょう。
軸が定義域内にあるとき
- 下に凸のグラフなら、頂点のｙ座標が最小値
- 上に凸のグラフなら、頂点のｙ座標が最大値
軸が定義域の左側にあるとき
- 下に凸のグラフなら、グラフの左端にある点のｙ座標が最小値、右端にある点のｙ座標が最大値
- 上に凸のグラフなら、グラフの左端にある点のｙ座標が最大値、右端にある点のｙ座標が最小値
軸が定義域の右側にあるとき
- 下に凸のグラフなら、グラフの左端にある点のｙ座標が最大値、右端にある点のｙ座標が最小値
- 上に凸のグラフなら、グラフの左端にある点のｙ座標が最小値、右端にある点のｙ座標が最大値
場合分けの必要な問題を解いてみよう
次の問題を解いてみましょう。
問の解答・解説
問
次の $2$ 次関数の最大値、最小値を求めよ。
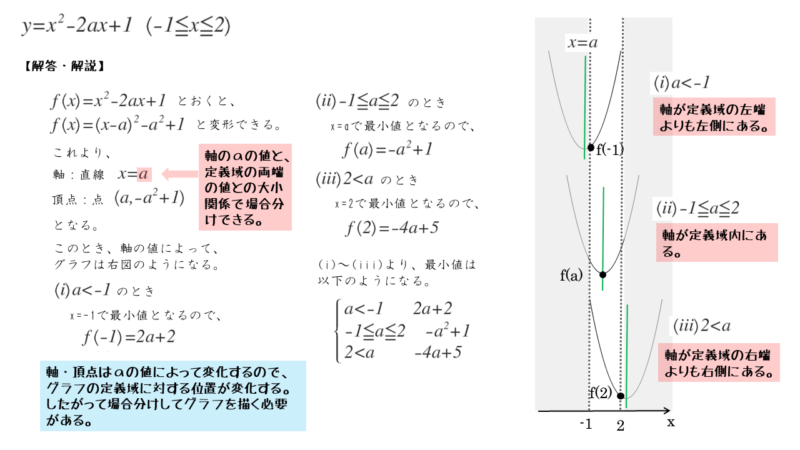
\begin{align*} \quad y={x}^{2}-2ax+1 \quad \left(-1 \leqq x \leqq 2 \right) \end{align*}場合分けが必要な問題であっても、最初にやることは与式を標準形に変形することです。
与式を平方完成して、軸・頂点・凸の情報を確認します。未知の定数ａがあるので注意しましょう。
問の解答例（最小値）
与式を変形して
\begin{align*} \quad y &= {x}^{2}-2ax +1 \\[ 7pt ] &= {\left( x-a \right)}^{2} -{a}^{2}+1 \end{align*}よって
頂点 … $( a \ , \ -{a}^{2}+1 )$
軸 … 直線 $x=a$
向き … 下に凸
標準形に変形した結果から分かるように、軸の方程式がｘ＝ａで、未知の定数ａが用いられています。ですから、定数ａの値によって軸の位置が変わります。
このとき、定義域に対するグラフの位置が変わるので、最大値や最小値をとる点も一意に定まりません。つまり、場合によって最大値や最小値が変わるということです。ですから、定数ａの値によって場合分けが必要になるのです。
軸の方程式（または定義域）に未知数が含まれると、定義域に対するグラフの位置が変わってしまう。
場合分けと言っても決まったパターンがあるので慣れれば簡単です。軸と定義域との位置関係は３パターンあります。凸の向きに関わらず、基本的には軸が定義域に入るか入らないかで場合分けします。
最大値と最小値を一緒に考えるのは混乱の元なので、分かりやすい最小値から考えます。
下に凸のグラフでは最小値から求めよう
下に凸のグラフでは、頂点のｙ座標が最小値となる可能性が高いです。しかし、頂点、つまり軸が定義域の外にあると、頂点のｙ座標が最小値になりません。
このことを考慮すると、以下の３パターンで場合分けできます。
下に凸のグラフでの最小値
- （軸ｘ＝ａが定義域外で左側にあるとき）⇒（軸ａの値が定義域の左端ｘ＝－１よりも小さいとき）
- （軸ｘ＝ａが定義域内にあるとき）⇒（軸ａの値は定義域の左端ｘ＝－１以上で右端ｘ＝２以下であるとき）
- （軸ｘ＝ａが定義域外で右側にあるとき）⇒（軸ａの値は定義域の右端ｘ＝２よりも大きいとき）
本来は先に作図を済ませるのがスムーズに記述するコツです。
定数ａの値が分からないので、作図するのが難しそうに感じますが、そんなことはありません。軸と定義域との位置関係だけを意識して作図します。
作図の手順は以下の通りです。
３パターンの作図の手順
- 定義域が分かるように両端から破線を引く（図ではｘ軸から上に引いた）
- 軸だけを定義域に対して３パターンに合わせて線を引く（図では緑色の線）
- グラフを軸に対して左右対称になるように書き込む
- 最小値をとる点が分かるように●をつける
このような手順で作図すると、グラフが左から順に移動したように描けるはずです。
３つの場合から、ａについての不等式が場合分けの条件となることが分かります。定数ａの値が定まらなければ、２次関数の最大値や最小値を求めることができないのですから当然です。
また、場合分けの条件式を導出するには、グラフを見ながら導出すると良いでしょう。
３パターンのグラフを描いてから、それぞれの場合の条件式を導出しよう。
最小値を求めるときのポイントと解答例をまとめると以下のようになります。
下に凸のグラフでの最大値は異なる3パターン
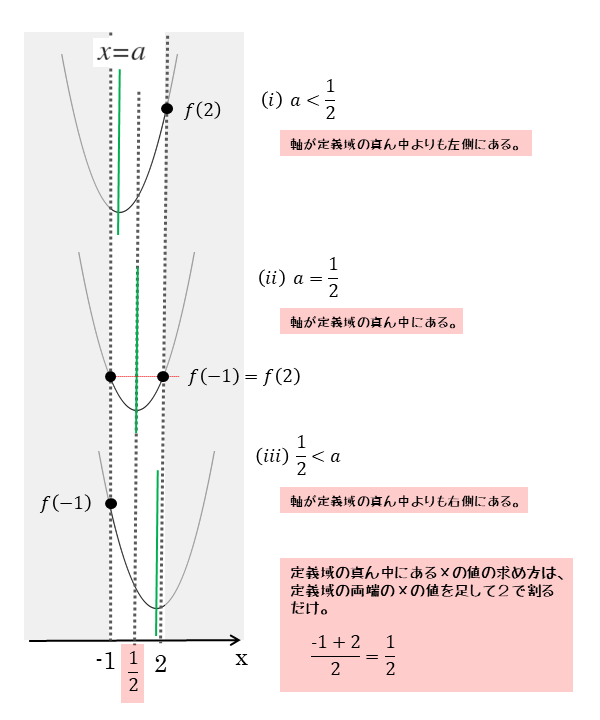
最大値も３パターンで場合分けできますが、最小値のときとは軸と定義域との位置関係が少し異なります。
軸と定義域の真ん中との位置関係で場合分けします。定義域の真ん中とは、－１≦ｘ≦２であれば、ｘ＝１/２が定義域の真ん中になります。
定義域の真ん中になるｘの値
与えられた定義域から、その真ん中は
\begin{align*} \quad \frac{-1+2}{2} = \frac{1}{2} \end{align*}※定義域の両端の $x$ の値を足して $2$ で割れば良い。
定義域の真ん中にあるｘの値が分かったので、以下の３パターンで場合分けできます。
下に凸のグラフでの最小値
- （軸ｘ＝ａが定義域の真ん中より左側にあるとき）⇒（軸ａの値が定義域の真ん中ｘ＝１/２よりも小さいとき）
- （軸ｘ＝ａが定義域の真ん中にあるとき）⇒（軸ａの値は定義域の真ん中ｘ＝１/２に等しい）
- （軸ｘ＝ａが定義域の真ん中より右側にあるとき）⇒（軸ａの値は定義域の右端ｘ＝１/２よりも大きいとき）
最大値の場合、２つ目が少し特殊なので注意しましょう。最大値をとる点がグラフの両端にできます。
この３つのパターンで場合分けすると、ａについての不等式を条件としてそれぞれ導出することができます。
最大値を求めるときの場合分け（下に凸のグラフ）
軸と定義域との位置関係から
\begin{align*} &(i) \ a \lt \frac{1}{2} \ \text{のとき} \\[ 5pt ] &x=2 \ \text{のとき、$2$ 次関数は最大値をとる。} \\[ 5pt ] &\text{よって、最大値は} \\[ 5pt ] &\quad f(2)=2^{2}-2a \cdot 2+1=-4a+5 \end{align*} \begin{align*} &(ii) \ a = \frac{1}{2} \ \text{のとき} \\[ 5pt ] &x=-1 \ \text{または} \ x=2 \ \text{のとき、$2$ 次関数は最大値をとる。} \\[ 5pt ] &\text{よって、最大値は} \\[ 5pt ] &\quad f(-1)=f(2)=2^{2}-2 \cdot \frac{1}{2} \cdot 2+1=3 \end{align*} \begin{align*} &(iii) \ \frac{1}{2} \lt a \ \text{のとき} \\[ 5pt ] &x=-1 \ \text{のとき、$2$ 次関数は最大値をとる。} \\[ 5pt ] &\text{よって、最大値は} \\[ 5pt ] &\quad f(-1)=\left(-1 \right)^{2}-2a \cdot \left(-1 \right)+1=2a+2 \end{align*}$(i)$ ～ $(iii)$ より \begin{align*} \begin{cases} -4a+5 & ( a \lt \frac{1}{2} ) \\ 3 & ( x = \frac{1}{2} ) \\ 2a+2 & ( \frac{1}{2} \lt a ) \end{cases} \end{align*}
３パターンで場合分けするときの作図の手順は以下の通りです。
３パターンの作図の手順
- 定義域が分かるように両端から破線を引く（図ではｘ軸から上に引いた）
- 定義域の真ん中にあるｘの値を求めておく。
- 軸だけを定義域に対して３パターンに合わせて線を引く（図では緑色の線）
- グラフを軸に対して左右対称になるように書き込む
- 最大値をとる点が分かるように●をつける
最小値のときと同様に、グラフが左から順に移動したように描けるはずです。
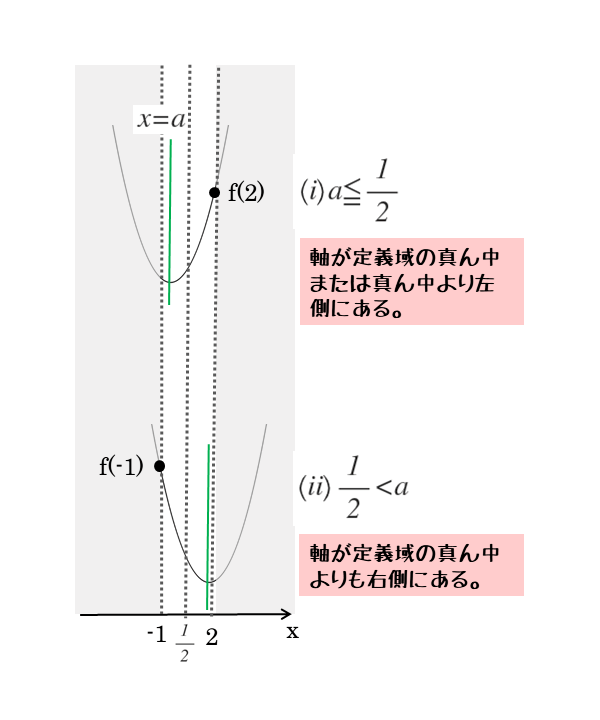
下に凸のグラフの最大値では２パターンの場合分けでも解ける
３つのパターンで場合分けしても全く問題ありませんが、２パターンで場合分けすることもできます。
２つ目を１つ目か３つ目のどちらかに含めてしまう場合分けです。
２つの場合分けになると、もっとすっきりした答案を作成できます。
要するに、軸が定義域の真ん中より右か左かで場合分けします。
ただし、ａについての不等式を２つ導出できますが、どちらかに等号を入れておくことを忘れないようにしましょう。
等号が入っていないと、すべてのａの値について吟味したことにならないからです。
最大値を求めるときのポイントと解答例をまとめると以下のようになります。解答例では２パターンの場合分けで解いています。
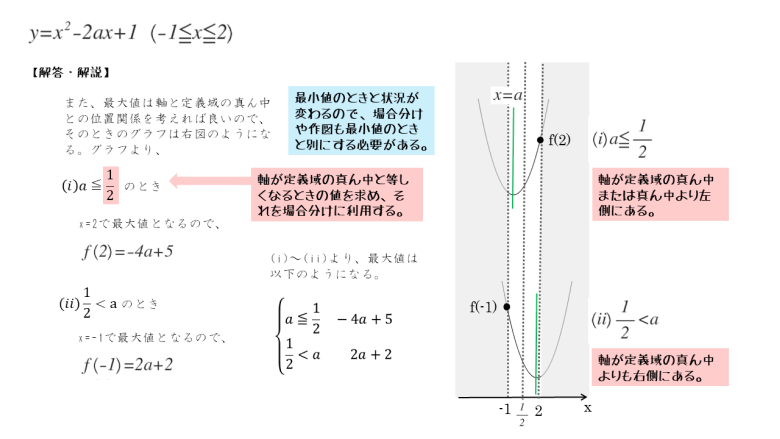
最大値と最小値は場合分けの仕方が異なるので別々に求めよう。また、軸と定義域との位置関係さえしっかりしていれば、グラフは精密でなくてもよい。
計算の処理能力はもちろん必要ですが、高校数学では作図の能力も必要になってきます。
作図ができると、初見の問題を解くときにかなり重宝します。作図しないときに比べて、イメージがより具体的になるでしょう。
問題によっては、余計な計算をせずに済んだり、「図より～」などと記述がラクになったりする場合もあります。
どんなときに作図が必要かを判断できなければ、解答・解説を見ると良い。近年の入試問題では、作図なしでは解くのが難しい問題の割合が増えているので注意しよう。
Recommended books
関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。
関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。
関数は、たとえば物理の直線運動でもｖ－ｔグラフなどで登場するので、ぜひとも攻略しておきたい単元です。
オススメその１
１冊目に紹介するのは『おもしろいほどよくわかる高校数学 関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。
高校数学で学ぶ２次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。
書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。
オススメその２
２冊目に紹介するのは『改訂版 坂田アキラの２次関数が面白いほどわかる本』です。
『おもしろいほどよくわかる高校数学 関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。
高校数学の基幹分野である「２次関数」は坂田の解説でマスターせよ！
累計５０万部超の「坂田理系シリーズ」の「２次関数」。２００９年４月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「２次関数」対策の決定版！！ 旧版になかった「解の配置」のテーマを増設。
教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。
オススメその３
２次関数は、高校数学で学習する関数の中で最も基本的なものです。ですから、苦手意識をもたないようにしっかりと取り組んでおいた方が良いでしょう。
参考書や問題集を上手に利用しましょう。その他にも以下のような教材があります。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度、頭の中を整理しよう
- 平方完成して、軸・頂点・凸の情報を確認する。
- 場合分けが必要な場合、パターンごとにグラフを書き分ける。
- 軸と定義域の位置関係から $x$ の不等式を作り、それを場合分けの条件式とする。
- 定義域内のグラフをもとに、最大値や最小値をとる点のｙ座標を求める。
- これらを整理して記述すれば、答案完成。
- 作図する習慣を付ける。