２次関数｜２次関数の決定について

04/21/2022数学１

今回は、２次関数の決定について学習しましょう。

２次関数の決定というのは、「関数の式を決定しましょう」ということです。ですから、２次関数の式についての知識を予め把握しておくことが大切です。

２次関数の決定に関する問題では、頂点・軸・凸の情報やグラフ上の点の座標などの各種情報が与えられます。これらの情報の使い方や使う際のポイントなどをしっかりマスターしましょう。

記事の画像が見辛いときはクリックすると拡大できます。

1. ２次関数の決定は式の定数の決定
2. ２次関数の決定までの流れ
3. ２次関数の決定に関する問題を解いてみよう
- 3.1. 問１の解答・解説
- 3.2. 問２の解答・解説
4. 文章中にヒントが必ずあるので、諦めてはダメです！
5. Recommended books
6. さいごに、もう一度、頭の中を整理しよう

２次関数の決定は式の定数の決定

２次関数の決定とは、グラフに関する情報をもとに式を決定することです。難しそうですがそうでもありません。

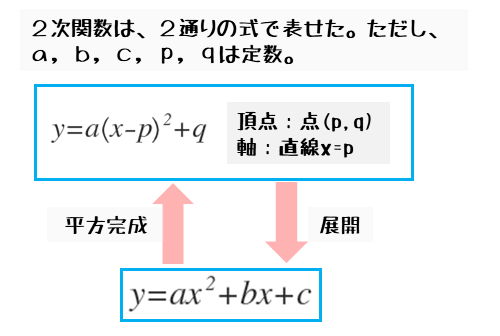
なぜなら、２次関数の式の形には「一般形」と「標準形」の２種類しかないからです。必ずどちらかの式で表せます。

２次関数の式は２種類

\begin{align*} &\quad y = ax^{2} +bx +c \ \text{（一般形）} \\[ 7pt ] &\quad y = a \left( x-p \right)^{2} +q \ \text{（標準形）} \end{align*}

ですから、２次関数の決定とは、結局のところ、係数や定数項などの定数ａ，ｂ，ｃ，ｐ，ｑを決定すると言った方が適切かもしれません。

定数の値を求めるためには、方程式を導出すればよい。与えられた情報から、求めたい定数についての方程式を導出しよう。

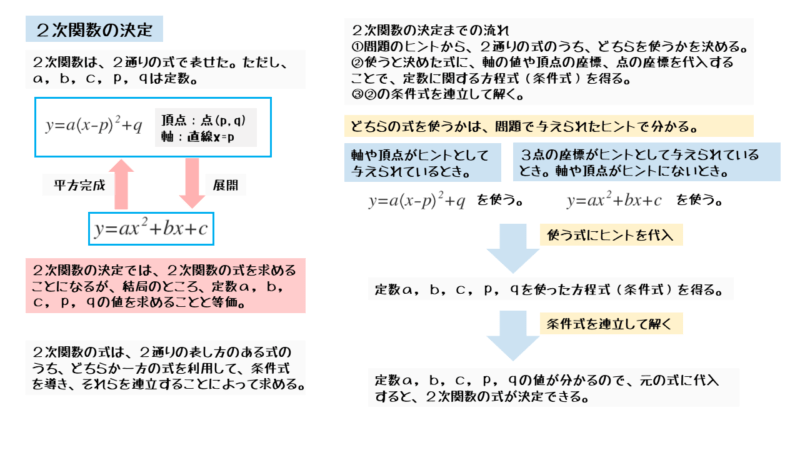
２次関数の決定までの流れ

２次関数の決定に関する問題は、たとえば、以下のような問題です。

問題文を確認すると、軸・頂点の情報やグラフ上の点の座標などの各種情報が与えられています。このような情報を用いて、２次関数の式を決定します。

大まかな手順は以下のようになります。

２次関数の式を決定する大まかな手順

与えられた情報から、式の形を決める
情報を式に代入して、方程式をいくつか導出
方程式を連立して、定数の値を求める

手順１式の形を決めよう

２次関数の式には、一般形と標準形の２種類あります。ですから、どちらの形で表した方が良いのかを最初に決めましょう。

これは自分で決めるというよりも、与えられた情報で決まってしまいます。ですから、与えられた情報をしっかり読み取ることが大切です。

ここで、一般形と標準形から、どんな情報が読み取れたのかを思い出してみましょう。

一般形の場合、定数ａの正負から凸の向きを読み取ることはできますが、軸や頂点の情報を読み取ることはできません。

問題を解くことに関して言えば、一般形を使うのは、点のｘ座標やｙ座標を求めるときくらい。標準形に変形してしまうことがほとんど。

基本的に、２次関数では標準形で考えていくことがほとんどです。ですから、「標準形が使えるかどうか」という視点に立っていれば良いでしょう。

標準形を使う場合、問題文には「軸」「頂点」などの文言が出てきます。軸や頂点などの用語が出てきたら、迷わず標準形で進めていきましょう。

それに対して、一般形を使う場合、グラフ上の３点の情報が与えられていることがほとんどです。

一般形と標準形の選択

一般形 … 問題文に３点の座標の情報があるとき
標準形 … 問題文に軸や頂点の情報があるとき

「標準形が使えそうになければ、一般形を使う」という方針であれば、たいてい上手くいくでしょう。

手順２情報を用いて方程式を導出しよう

一般形と標準形の選択が終わったら、与えられた情報を用いて方程式を導出します。情報が複数あるので、方程式もそれに応じた数だけ導出できます。

たとえば、３点の座標が与えられているとします。

この場合、３点の座標を一般形にそれぞれ代入すると、３つの方程式を導出できます。一般形では、求めたい定数はａ，ｂ，ｃの３つなので、方程式も３つ必要になります。

未知数のぶんだけ、方程式（条件式）が必要になる。点の座標が与えられていれば、とりあえず関数の式に代入してみよう。

手順３方程式を連立して解こう

情報を使って方程式を導出できたら、方程式を連立して解きます。これで得られた解が、求めたい定数ａ，ｂ，ｃ，ｐ，ｑの値です。

「与えらた情報から式の形を決定し、情報と式を利用して方程式（条件式）を導出し、それらを連立して解く」、このような手順で２次関数の式を決定します。

これまでをまとめると以下のようになります。

２次関数の決定に関する問題を解いてみよう

先ほど例に挙げた問題を解いてみましょう。

問１の解答・解説

問１

次の条件を満たす $2$ 次関数を求めよ。

グラフの頂点が $(2 \ , \ 1)$ で、点 $(1 \ , \ -1)$ を通る。

問題文から読み取った情報を整理してみましょう。

問１で与えられた情報

グラフの頂点 … $(2 \ , \ 1)$

グラフが通る点 … 点 $(1 \ , \ -1)$

「頂点」という文言が出てきたので、式の形は「標準形」に決定です。

標準形の定数ｐ，ｑの値は、頂点の座標が分かった時点でＰ＝２，ｑ＝１と分かります。求める必要がなくなったので、標準形に代入しておきます。

問１の解答例 1⃣

求める $2$ 次関数の式を

\begin{align*} \quad y=a\left(x-p \right)^{2}+q \end{align*}

とおくと、頂点が点 $(2 \ , \ 1)$ であるので

\begin{align*} \quad p=2 \ , \ q=1 \end{align*}

よって

\begin{align*} \quad y=a\left(x-2 \right)^{2}+1 \quad \cdots \text{①} \end{align*}

と表せる。

軸や頂点の情報が与えられている場合、それらの情報を標準形に代入した式をスタートの式として使っていきましょう。①式を導出できないと先に進めません。

定数ｐ，ｑの値は予め与えられていたので、実質、定数ａの値を求めるだけになります。

点の座標(１，－１)が与えられていたので、これを①式に代入します。すると、定数ａについての１次方程式を導出できるので、これを解きます。

問１の解答例 2⃣

\begin{align*} \quad &\vdots \\[ 7pt ] \quad y &=a\left(x-2 \right)^{2}+1 \quad \cdots \text{①} \\[ 7pt ] \quad &\vdots \end{align*}

グラフは点 $(1 \ , \ -1)$ を通るので、①より

\begin{align*} \quad -1 =a\left(1-2 \right)^{2}+1 \end{align*}

$a$ について解くと

\begin{align*} \quad -1 &=a+1 \\[ 7pt ] \quad a &=-2 \end{align*}

これを①に代入すると、求める式は

\begin{align*} \quad y =-2\left(x-2 \right)^{2}+1 \end{align*}

上述の解答例では、標準形のままにしていますが、展開しても構いません。

問１のポイントと解答例をまとめると以下のようになります。

問２の解答・解説

問２

次の条件を満たす $2$ 次関数を求めよ。

グラフが $3$ 点 $(0 \ , \ -3) \ , \ (-1 \ , \ 0) \ , \ (1 \ , \ 4)$ を通る。

問題文から読み取った情報を整理してみましょう。

問２で与えられた情報

グラフが通る $3$ 点 … 点 $(0 \ , \ -3) \ , \ (-1 \ , \ 0) \ , \ (1 \ , \ -4)$

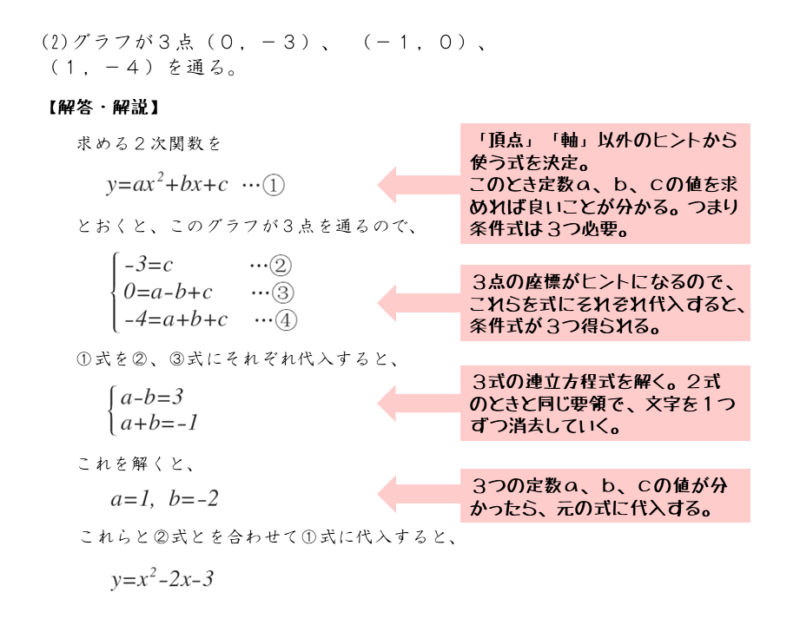
頂点や軸の情報がなく、グラフ上の３点の座標が与えられています。標準形が使えないので、式の形は「一般形」に決定です。

求める２次関数の式は、３点の座標を代入したときに等式が成り立つ式です。このことを利用します。

３点の座標を一般形にそれぞれ代入します。すると、定数ａ，ｂ，ｃについての方程式を導くことができるので、これらを連立して解きます。

問２の解答例 1⃣

求める $2$ 次関数の式を

\begin{align*} \quad y=ax^{2}+bx+c \quad \cdots \text{①} \end{align*}

とおくと、点 $(0 \ , \ -3)$ を通るので

\begin{align*} \quad -3 &=c \\[ 7pt ] \quad c &=-3 \quad \cdots \text{②} \end{align*}

また、点 $(-1 \ , \ 0)$ を通るので

\begin{align*} \quad 0 =a \cdot \left(-1 \right)^{2}+b \cdot \left(-1 \right)+c \end{align*}

整理すると

\begin{align*} \quad a-b+c &=0 \quad \cdots \text{③} \end{align*}

さらに、点 $(1 \ , \ -4)$ を通るので

\begin{align*} \quad -4 &=a \cdot 1^{2}+b \cdot 1+c \\[ 7pt ] \end{align*}

整理すると

\begin{align*} \quad a+b+c &=-4 \quad \cdots \text{④} \end{align*}

求めたい定数ａ，ｂ，ｃを用いた方程式（条件式）を３つ導出できました。

グラフが３点を通るためには、これらの方程式をすべて満たさなければなりません。ですから、連立方程式の解が、求めたい定数ａ，ｂ，ｃの値になります。

問２の解答例 2⃣

\begin{align*} &\quad y=ax^{2}+bx+c \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad c =-3 \quad \cdots \text{②} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a-b+c =0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a+b+c =-4 \quad \cdots \text{④} \end{align*}

②を③，④にそれぞれ代入すると

\begin{align*} \quad a-b &=3 \quad \cdots \text{③’} \\[ 7pt ] \quad a+b &=-1 \quad \cdots \text{④’} \end{align*}

これらを連立して解くと、③’＋④’より

\begin{align*} \quad 2a=2 \end{align*}

よって

\begin{align*} \quad a=1 \end{align*}

これと④’より

\begin{align*} \quad 1+b =-1 \end{align*}

よって

\begin{align*} \quad b =-2 \end{align*}

したがって、求める式は①より

\begin{align*} \quad y=x^{2}-2x-3 \end{align*}

②式を上手に使えば、③，④式からｃを消去することができます。その結果、定数ａ，ｂについての方程式を２つ導くことができます。

２つの式を連立して解くのは難しくないでしょう。これを解くと、定数ａ，ｂの値が分かります。

連立方程式を解くとき、②式のように、３つの定数のうち１つはすぐに分かることが多い。連立方程式の解き方のコツは、代入法や加減法を利用して文字の数を減らしていくこと。

問２のポイントと解答例をまとめると以下のようになります。

問２のような一般形を利用する問題になると、計算量が多くなります。計算ミスなく解けるようにしておきましょう。

文章中にヒントが必ずあるので、諦めてはダメです！

基本的に、求めたい値の数に合わせて、ヒントも同じ数だけ与えられます。方程式を導くのために必要だからです。ですから、簡単に諦めてはいけません。

もちろん、難易度の高い問題になると、同意表現が使われていて分かりにくいこともありますが、最初のうちは基礎から標準レベルの問題できちんと読み取る訓練をすることが大切です。

このことを知っていることで、初見の問題に出会ったときでも解法の糸口を掴めるかもしれません。

求めたい値の数に応じて条件式が必要。これを知っていると突破口が見えてくるかもしれない。

Recommended books

関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。

関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。

関数は、たとえば物理の直線運動でもｖ－ｔグラフなどで登場するので、ぜひとも攻略しておきたい単元です。

オススメその１

１冊目に紹介するのは『おもしろいほどよくわかる高校数学関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。

高校数学で学ぶ２次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。

書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。

おもしろいほどよくわかる高校数学関数編

created by Rinker

オススメその２

２冊目に紹介するのは『改訂版坂田アキラの２次関数が面白いほどわかる本』です。

『おもしろいほどよくわかる高校数学関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。

高校数学の基幹分野である「２次関数」は坂田の解説でマスターせよ！
累計５０万部超の「坂田理系シリーズ」の「２次関数」。２００９年４月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「２次関数」対策の決定版！！旧版になかった「解の配置」のテーマを増設。

教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。