２次関数｜２次関数のグラフの平行移動について
前回の記事でこれまでに学習した比例や反比例などの関数について復習ました。関数の式とグラフの関係を関連付けておくことが大切でした。
今回は高校数学の関数においてメインで扱う２次関数について学習します。
２次関数のグラフの平行移動
グラフの平行移動とは、グラフをｘ軸方向やｙ軸方向に沿って移動させることです。
グラフの平行移動では、直線の傾きが変わったり、曲線の曲がり具合が変わったりすることはないので注意しましょう。ただ単に、グラフの位置が変わるだけです。
高校数学で学習する２次関数の式は、グラフの平行移動に関係しています。２乗に比例する関数のグラフを平行移動すると、２次関数の標準形と呼ばれる式が導かれるからです。
２次関数のグラフは、中学で学習した２乗に比例する関数のグラフを平行移動したもの。２乗に比例する関数は、２次関数の一例。
ですから２次関数の式やグラフを扱えるように、２乗に比例する関数に関する事柄を予めマスターしておく必要があります。
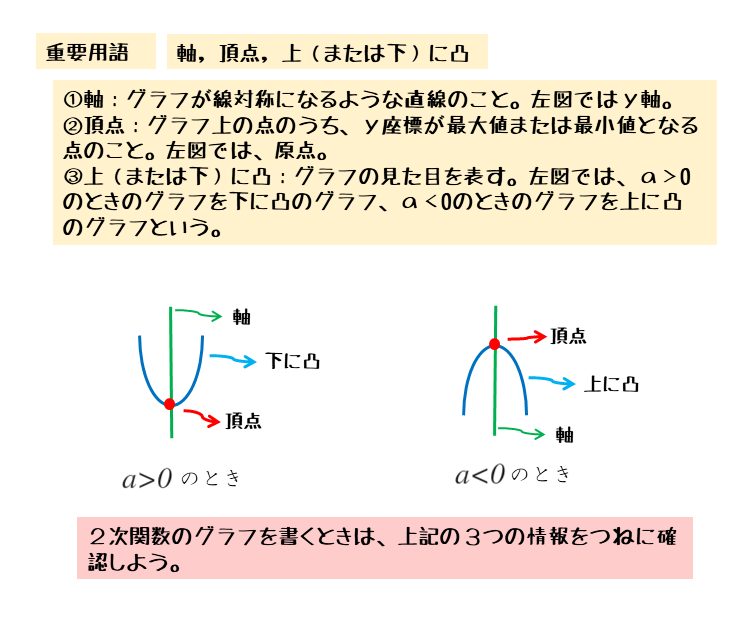
グラフの概形や用語も確認しておきましょう。
２乗に比例する関数のグラフを平行移動するやり方は３パターンあります。
２乗に比例する関数のグラフを平行移動するやり方
- グラフをｙ軸方向に平行移動する
- グラフをｘ軸方向に平行移動する
- グラフをｙ軸方向およびｘ軸方向に平行移動する
３番目は１，２番目の平行移動を組み合わせたものなので、１，２番目の平行移動をきちんと理解しましょう。
ｙ軸方向の平行移動
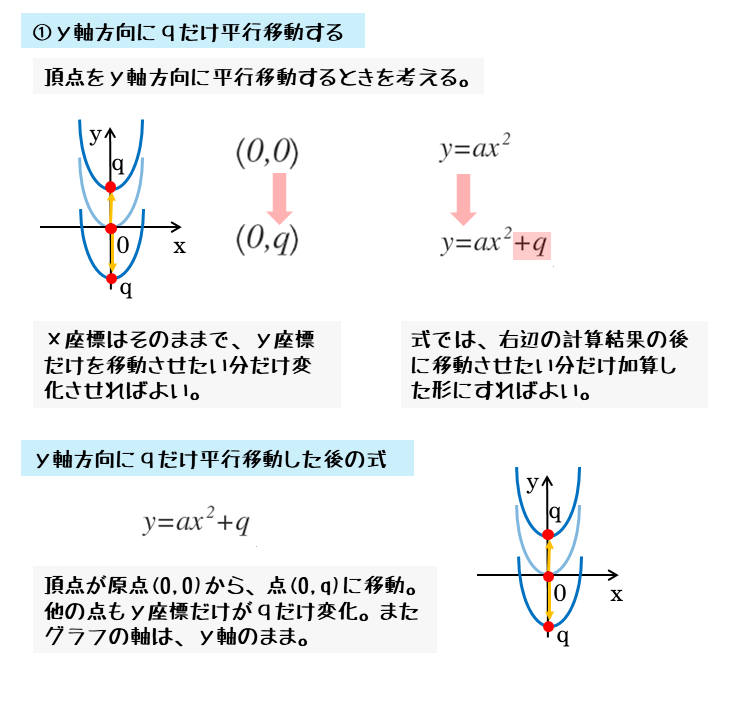
２乗に比例する関数ｙ＝ａｘ2のグラフをｙ軸方向（上下方向）にｑだけ平行移動してみましょう。
このとき、原点にある頂点(０，０)はｙ軸方向にｑだけ平行移動します。すると、頂点の座標は(０，ｑ)に移動します。
ｙ軸方向の平行移動では、ｘ座標は変わらず、ｙ座標が平行移動の分だけ変化。
頂点以外の点も同じように、すべてがｙ軸方向にｑだけ平行移動するので、座標もｙ座標だけがｑだけ変化します。
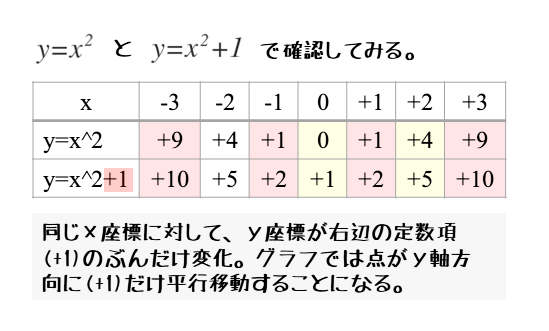
このような平行移動をしたとき、移動後の式は右辺に定数項ｑが加わった式に変わります。
ｙ軸方向にｑだけ平行移動したとき
$y=ax^2$ のグラフを $y$ 軸方向に $q$ だけ平行移動する。
\begin{align*} &\text{移動前の式} \ \cdots \ y = ax^2 \\[ 7pt ] &\text{移動後の式} \ \cdots \ y = ax^2 \underline{+q} \end{align*}
ｙ軸方向の平行移動は、式では右辺の定数項に反映されます。ただし、頂点の座標は変わりましたが、軸や凸の向きは変化しません。
ｙ軸方向にｑだけ平行移動したとき
\begin{align*} &\text{移動後の式} \ \cdots \ y = ax^2 +q \\[ 7pt ] &\text{頂点} \ \cdots \ \text{原点から点} \ (0 \ , \ q) \ \text{に移動} \\[ 7pt ] &\text{軸} \ \cdots \ \text{$y$ 軸で変わらず} \\[ 7pt ] &\text{凸の向き} \ \cdots \ \text{変わらず} \end{align*}具体例から分かるように、同じｘの値に対して、ｙの値だけが平行移動の分だけ変化しています。
グラフ上にある点のｙ座標が変化するのに伴って、グラフはｙ軸方向に平行移動します。
２次関数のグラフの平行移動では、グラフの位置が変わるだけで、移動の前後で比例定数ａの値は変わらない。比例定数ａは凸の向きやグラフの開き具合を表す値。
ｘ軸方向の平行移動
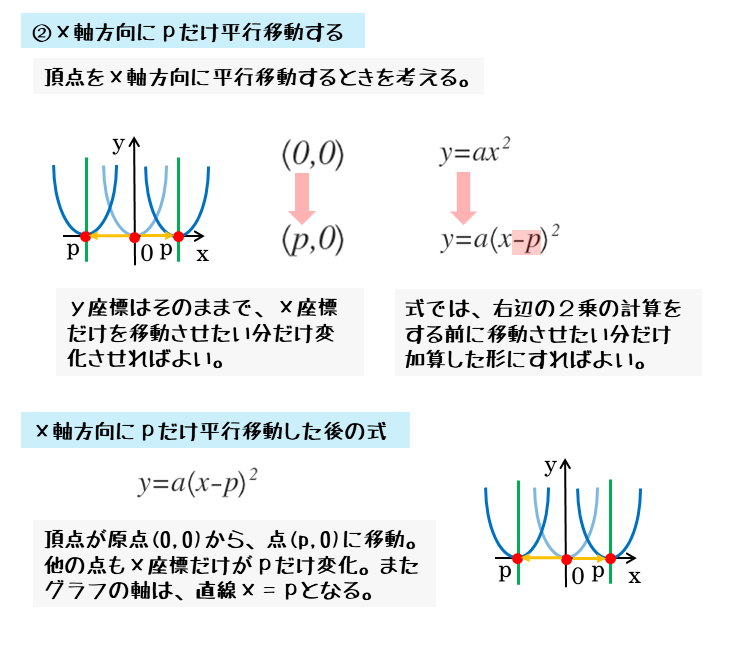
２乗に比例する関数ｙ＝ａｘ2のグラフをｘ軸方向（左右方向）にｐだけ平行移動してみましょう。
このとき、原点にある頂点(０，０)はｘ軸方向にｐだけ平行移動します。すると、頂点の座標は(ｐ，０)に移動します。
ｘ軸方向の平行移動では、ｙ座標は変わらず、ｘ座標が平行移動の分だけ変化。
頂点以外の点も同じように、すべてがｘ軸方向にｐだけ平行移動するので、座標もｘ座標だけがｐだけ変化します。
このような平行移動をしたとき、移動後の式は右辺のｘが(ｘ－ｐ)に置き換わった式に変わります。
ｘ軸方向にｐだけ平行移動したとき
$y=ax^2$ のグラフを $x$ 軸方向に $p$ だけ平行移動する。
\begin{align*} &\text{移動前の式} \ \cdots \ y = ax^2 \\[ 7pt ] &\text{移動後の式} \ \cdots \ y = a\left( x \underline{-p} \right)^2 \end{align*}
ｘ軸方向の平行移動は、式では右辺の変数ｘに反映されます。ただし、頂点の座標とともに軸の位置が変わりますが、凸の向きは変化しません。
特に注意したいのは、軸の位置です。軸はグラフにおいて対称の軸であり、頂点を必ず通ります。軸と頂点の関係から、頂点がｘ軸方向に平行移動すると、それに伴って軸もｘ軸方向に平行移動します。
ｘ軸方向にｐだけ平行移動したとき
\begin{align*} &\text{移動後の式} \ \cdots \ y = a\left( x-p \right)^2 \\[ 7pt ] &\text{頂点} \ \cdots \ \text{原点から点} \ (p \ , \ 0) \ \text{に移動} \\[ 7pt ] &\text{軸} \ \cdots \ \text{直線 $x=p$ に移動} \\[ 7pt ] &\text{凸の向き} \ \cdots \ \text{変わらず} \end{align*}具体例から分かるように、同じｙの値に対してｘの値だけが平行移動の分だけ変化しています。
グラフ上にある点のｘ座標が変化するのに伴って、グラフはｘ軸方向に平行移動します。
ｙ軸方向およびｘ軸方向の平行移動
ｙ軸方向およびｘ軸方向の平行移動は、これまでの２つの平行移動を合わせた移動です。
ここで注意したいのは、混乱の元となるので同時に平行移動させないことです。たとえば、ｙ軸方向に平行移動してからｘ軸方向に平行移動させるなどします。そうすると平行移動後のグラフの位置が分かります。
２乗に比例する関数ｙ＝ａｘ2のグラフをｘ軸方向にｐだけ、ｙ軸方向にｑだけ平行移動したときの式は以下のようになります。また、頂点や軸についてもまとめておきます。
ｘ軸方向にｐだけ、ｙ軸方向にｑだけ平行移動したとき
$y=ax^2$ のグラフを $x$ 軸方向に $p$ だけ平行移動する。
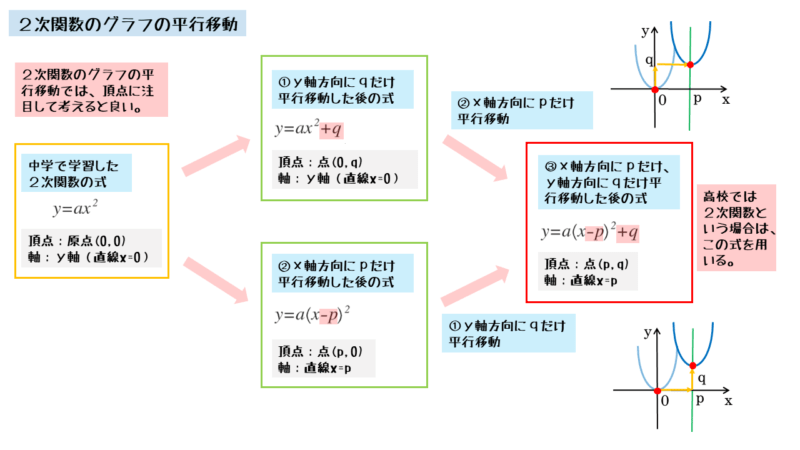
\begin{align*} &\text{移動前の式} \ \cdots \ y = ax^2 \\[ 7pt ] &\text{移動後の式} \ \cdots \ y = a\left( x \underline{-p} \right)^2 \underline{+q} \ \text{（この式を標準形と言う）} \\[ 7pt ] &\text{頂点} \ \cdots \ \text{原点から点} \ (p \ , \ q) \ \text{に移動} \\[ 7pt ] &\text{軸} \ \cdots \ \text{直線 $x=p$ に移動} \\[ 7pt ] &\text{凸の向き} \ \cdots \ \text{変わらず} \end{align*}ｘ軸方向とｙ軸方向とで式の変わる箇所が決まっているので、対応関係を把握しましょう。２次関数のグラフの平行移動をまとめると以下のようになります。
グラフの平行移動は、式の形を見て判断しよう。
なお、関数ｙ＝ａｘ2をｘ軸方向およびｙ軸方向に平行移動して得られる式ｙ＝ａ(ｘ－ｐ)2＋ｑを「２次関数の標準形」として用います。
２次関数を扱うとき、標準形の式で考えるのが基本です。この式から「軸・頂点・凸の向き」の３つの情報を得ることができるようにしておきましょう。
２乗に比例する関数と２次関数との関係をまとめると以下のようになります。２乗に比例する関数は、２次関数の一例と考えることができます。
グラフの平行移動を一般化する
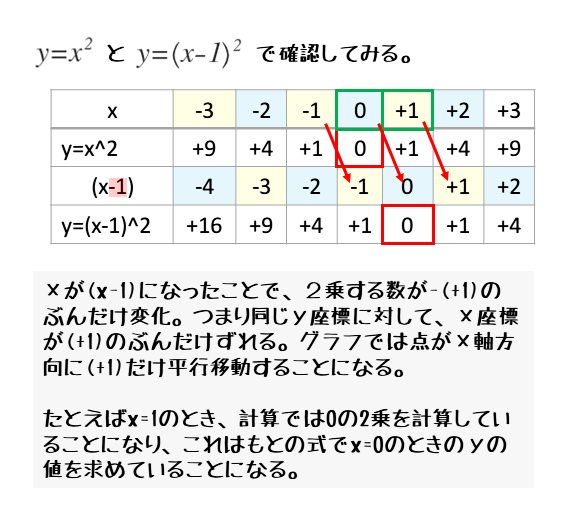
２乗に比例する関数ｙ＝ａｘ2のグラフをｘ軸方向にｐだけ平行移動すると、式がｘから(ｘ－ｐ)に置き換えた形に変わりました。
この置き換えは、ｙ軸方向の平行移動でも成り立ちます。
ｙ軸方向にｑだけ平行移動したとき
$y=ax^2$ のグラフを $y$ 軸方向に $q$ だけ平行移動させる。
\begin{align*} \quad y=ax^2 \end{align*}において、$y$ を $y-q$ に置き換えると
\begin{align*} \quad y-q=ax^2 \end{align*}よって
\begin{align*} \quad y=ax^2 +q \end{align*}このことから分かるのは、グラフを平行移動した後の式は、ｘやｙを平行移動のぶんを考慮した式に置き換えるだけで求めることができるということです。
グラフの平行移動の一般化
- ｘ軸方向にｐだけ平行移動 ⇒ ｘを(ｘ－ｐ)に置き換える
- ｙ軸方向にｑだけ平行移動 ⇒ ｙを(ｙ－ｑ)に置き換える
このことは、２次関数だけではなく関数全般で成り立ちます。この性質を上手に利用できるようになると、どんな関数でも平行移動後の式を簡単に求めることができます。
今後、三角関数、対数・指数関数、３次関数など様々な関数を学習する。２次関数の平行移動でマスターしておこう。
手順は非常に簡単です。ｘやｙを平行移動した分を考慮した式に置き換えるだけです。
置き換えた後に式を整理すると、平行移動後の式になります。
この性質の利点は、対応部分の置き換えだけで平行移動後の式を求めることができる点です。
平行移動後の式を求めるだけであれば、グラフの図示や標準形への変形が不要なので、かなり便利な性質です。
ｙ＝ｆ(ｘ)について
図解では、ｙ＝ｆ(ｘ)という式を用いています。ｆはfunction（関数）の頭文字です。
ｙ＝ｆ(ｘ)という式は、ｙがｘの関数であることを表します。ただし、ｙ＝ｆ(ｘ)だけは、具体的にどんな式であるのか分かりません。
たとえば、ｆ(ｘ)をｙの代わりに用いて、ｆ(ｘ)＝ｘ＋５のように記述します。ｆ(ｘ)を用いると、ｘの値とそれに対応するｙの値とを１つの式で扱えるようになります。
ｆ(１)＝６であれば、ｘ＝１のときｙ＝６であることを表します。ｘ＝１やｙ＝６だけでは、対応するｘやｙの値が分かりません。それに対してｆ(ｘ)を使うと、１つの式でｘ，ｙの値を両方とも知ることができます。
関数では、ｘ，ｙの値をセットで扱うので、１つの式で記述できるのはとても便利です。
２次関数のグラフの平行移動を扱った問題を解いてみよう
次の問題を考えてみましょう。
問の解答例・別解
問
次の $2$ 次関数のグラフを、$x$ 軸方向に $-2$、$y$ 軸方向に $1$ だけ平行移動したあとのグラフの式を求めよ。
\begin{align*} \quad y=x^2 +3 \end{align*}２次関数のグラフの平行移動に関する問題です。２次関数のグラフを平行移動する問題の基本的な解き方をまとめると以下のようになります。
２次関数のグラフの平行移動の基本的な解き方
- 与式を標準形にして頂点を求め、平行移動する。
- 移動後の頂点の座標を標準形の式に戻す。
与式は標準形で表されています。与式は、関数ｙ＝ｘ2のグラフをｙ軸方向に３だけ平行移動したときの式です。
与式と標準形（公式）の対応関係は以下のようになります。
与式と標準形（公式）の対応関係
\begin{align*} &\text{標準形} \ \cdots \ y = a\left( x-p \right)^2 +q \\[ 7pt ] &\text{与式} \ \cdots \ y=x^2 +3 \end{align*}対応関係を調べると
\begin{align*} \quad a=1 \ , \ p=0 \ , \ q=3 \end{align*}よって、与式の頂点の座標は
\begin{align*} \quad (0 \ , \ 3) \end{align*}対応関係が分かれば、平行移動後の頂点や軸などの情報もすぐに分かります。ただし、平行移動によって、凸の向きや開き具合に変化はないので、ａ＝１のままです。
２次関数のグラフの平行移動では、頂点に注目してグラフの平行移動を考えるのが基本です。ですから、与式が標準形になっているかを最初に確認しましょう。
頂点(０，３)をｘ軸方向に－２だけ、ｙ軸方向に１だけ平行移動します。
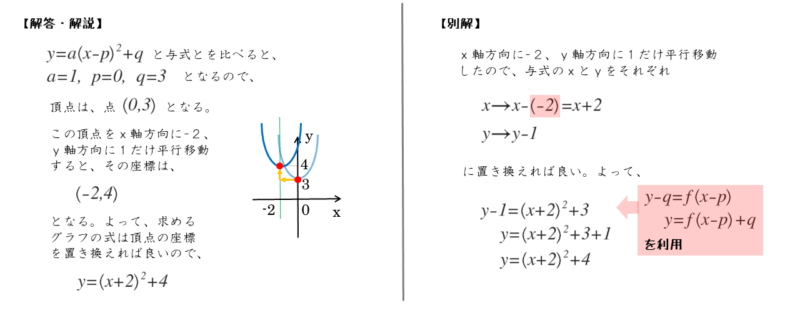
問の解答例 1⃣
与式から頂点の座標は
\begin{align*} \quad (0 \ , \ 3) \end{align*}$x$ 軸方向に $-2$、$y$ 軸方向に $1$ だけ平行移動すると
平行移動後の頂点の座標は
\begin{align*} \quad (-2 \ , \ 4) \end{align*}平行移動の頂点の座標が分かったら、２次関数の式を求めます。標準形（公式）に代入します。
標準形（公式）に代入するのは、ａ＝１，ｐ＝－２，ｑ＝４です。
問の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad (-2 \ , \ 4) \end{align*}よって、平行移動後の式は
\begin{align*} \quad y=\left\{ \underline{x-\left(-2 \right)} \right\}^2 +4 \end{align*}したがって
\begin{align*} \quad y=\left(x+2 \right)^2 +4 \end{align*}得られた式を展開する必要はありません。標準形のままで問題ありません。
また、ｐに負の値を代入するときは注意しましょう。ｐ＝－２を代入すれば下線部分のようになります。符号ミスが多いので気を付けましょう。
問の別解例
別解として、一般化したグラフの平行移動の考えを利用する解法もあります。応用的な解法になりますが、慣れるとかなり簡単に解けるようになります。
一般化したグラフの平行移動
$y=f(x)$ のグラフを $x$ 軸方向に $p$ だけ、$y$ 軸方向に $q$ だけ平行移動する。
このとき
\begin{align*} \quad y=f(x) \end{align*}において、$x$ を $x-p$ に、$y$ を $y-q$ に置き換えて
\begin{align*} \quad y-q=f \left(x-p \right)\end{align*}よって
\begin{align*} \quad y=f \left(x-p \right)+q \end{align*}ｆ(ｘ)を用いていても同じ要領で求めることができます。
平行移動の応用的な解法の手順
ｙ－ｑ=ｆ(ｘ－ｐ)を利用する。
- ｘを(ｘ－ｐ)に、ｙを(ｙ－ｑ)に置き換える。
- 置き換え後の式を整理する。
ｘ，ｙを平行移動に合わせた式に置き換えて整理します。
問の別解例
のグラフを $x$ 軸方向に $-2$、$y$ 軸方向に $1$ だけ平行移動するので
$x$ を $x-(-2)$、すなわち $x+2$ に、$y$ を $y-1$ に置き換えればよい。
よって、平行移動後の式は
\begin{align*} \quad y-1= \left(x+2 \right)^2 +3 \end{align*}整理すると
\begin{align*} \quad y = \left(x+2 \right)^2 +4 \end{align*}ｆ(ｘ)に相当するのはｘ2＋３です。この式においてｘをｘ＋２に置き換えます。＋３を忘れないようにしましょう。
応用的な解法は機械的に解くので、手順さえ覚えてしまえば簡単に利用できるようになります。ただ、２次関数では軸や頂点の情報を求めることが必須になります。ですから、最初のうちは基本的な解法で解くようにした方が無難でしょう。
問のポイントと解答例をまとめると以下のようになります。
２次関数のグラフの平行移動では、頂点の平行移動で解くのが基本。ただし、応用的な解法を利用すると、時間の短縮や負担の軽減になるので状況に応じて使い分けよう。
Recommended books
関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。
関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。
関数は、たとえば物理の直線運動でもｖ－ｔグラフなどで登場するので、ぜひとも攻略しておきたい単元です。
オススメその１
１冊目に紹介するのは『おもしろいほどよくわかる高校数学 関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。
高校数学で学ぶ２次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。
書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。
オススメその２
２冊目に紹介するのは『改訂版 坂田アキラの２次関数が面白いほどわかる本』です。
『おもしろいほどよくわかる高校数学 関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。
高校数学の基幹分野である「２次関数」は坂田の解説でマスターせよ！
累計５０万部超の「坂田理系シリーズ」の「２次関数」。２００９年４月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「２次関数」対策の決定版！！ 旧版になかった「解の配置」のテーマを増設。
教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。
オススメその３
２次関数は、高校数学で学習する関数の中で最も基本的なものです。ですから、苦手意識をもたないようにしっかりと取り組んでおいた方が良いでしょう。
参考書や問題集を上手に利用しましょう。その他にも以下のような教材があります。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度、頭の中を整理しよう
- ２次関数の標準形は、２乗に比例する関数のグラフの平行移動から得られる。
- ｙ軸方向とｘ軸方向の平行移動を個別に理解しよう。
- ｙ軸方向およびｘ軸方向に平行移動した後の式が、２次関数の標準形。
- 標準形から「軸・頂点・凸の向き」の３つの情報を取り出せるようにしよう。
- 関数のグラフの平行移動では、決まった置き換えで移動後の式を求めることができる。