数と式|整式の因数分解に関する問題を解いてみよう

整式の因数分解を扱った問題を解いてみましょう。問題を解くことでどこが理解できていないかが分かるので、ある程度学習したら、どんどん演習しましょう。
基礎レベルから応用レベルまでたくさん演習をこなして計算力を付けておきましょう。
式を見て解き方を判断できるレベルを目指そう
教科書を熟読したり、問題をたくさん解いたりしていくと、学習したことの意味や相互関係が徐々に分かってきます。習熟度が一定のレベルに上がったからです。
学習において、習熟度はとても大切な要素の1つです。習熟度が高くなれば、式を見ただけで方針が立つようになります。
特に、マーク形式の共通テスト(旧センター試験)は時間との闘いなので、式の扱いを考えている暇はありません。反射的に式変形できるようなレベルにしておくことが大切です。
展開や因数分解は、数学1の序盤で登場しますが、この後も様々な単元で必要な知識です。式を扱うときの基本的な知識になるので、誰よりも演習をこなして自信を付けておきましょう。
整式の因数分解に関する演習問題
次の整式を因数分解してみましょう。
問1の解答・解説
問1
次の式を因数分解せよ。
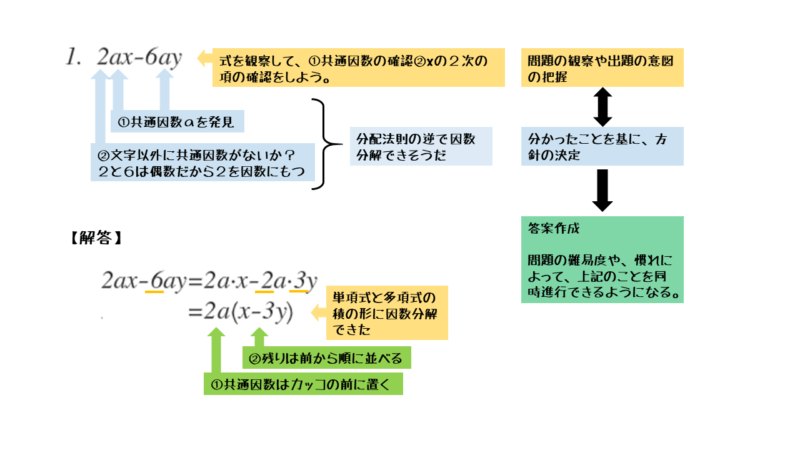
\begin{align*} \quad 2ax-6ay \end{align*}式をよく観察すると、以下のことが分かります。
与式をよく観察しよう
- 2ax,-6ayの2項からなる多項式
- 2次の項がない
- 各項に同じ文字aがある
同じ文字、つまり共通因数があるので、分配法則の逆で因数分解すれば良いことが分かります。
因数分解の基本は、共通因数でくくる分配法則の逆。与式を観察して、共通因数の有無を確認しよう。
なお、数が共通因数になるときは注意が必要です。
ここでは、6=2×3と因数分解できるので、2と6は共通因数2をもちます。つまり、与式は2aを共通因数をもつことから、aではなく2aでくくって因数分解しなければなりません。
数が共通因数になるとき、意外と見落としがちなので気を付けましょう。
与式を共通因数2aでくくって、因数分解します。
問1の解答例
与式を共通因数 $2a$ でくくると
\begin{align*} \quad 2ax-6ay =2a \left(x-y \right) \end{align*}共通因数でくくったら、カッコの中を確認しましょう。式によっては、さらに因数分解が必要なときがあります。
カッコの中を確認すると、1次式です。この1次式には共通因数がなく、また乗法公式にも当てはまらない式です。これ以上、与式を因数分解することはできないので、ここで終了です。
問1のポイントと解答例をまとめると以下のようになります。
共通因数を取り除いた後の式が1次式であれば、因数分解し終わったと考えてよい。
問2の解答・解説
問2
次の式を因数分解せよ。
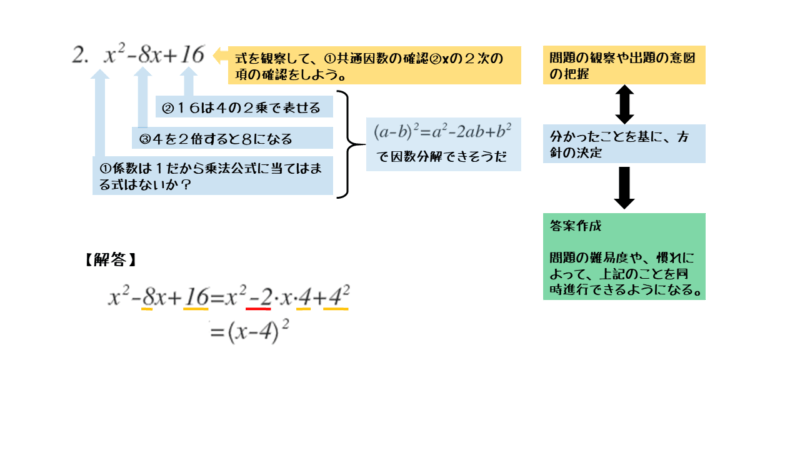
\begin{align*} \quad x^2 -8x+16 \end{align*}式をよく観察すると、以下のことが分かります。
与式をよく観察しよう
- x2,-8x,+16の3項からなる多項式
- 文字xについての2次式
- 2次の項の係数は1
- 各項に共通因数は見当たらない。
与式を見た時点で気づくと思いますが、本問は中学の因数分解に出てくる問題です。
乗法公式の中に、文字xについての1次式どうしの積で表される式があります。それを利用して因数分解します。
定数項+16(積)の因数の組み合わせを考え、その組み合わせが正しいかを1次の項-8xの係数-8(和)で確かめます。積が+16で和が-8になる数の組合せは、-4と-4です。
同じ数の組合せであるので、ここではカッコの2乗の公式を利用して、与式を因数分解します。
問2の解答例
積が $16$、和が $-8$ となる数の組合せから
\begin{align*} \quad x^2 -8x+16 =x^2 -2 \cdot 4x+4^2 \end{align*}よって
\begin{align*} \quad x^2 -8x+16 =\left(x-4 \right)^2 \end{align*}展開(因数分解)の前後の式を見比べよう。定数項(積)と1次の項の係数(和)との関係が分かる。
問2のポイントと解答例をまとめると以下のようになります。
問3の解答・解説
問3
次の式を因数分解せよ。
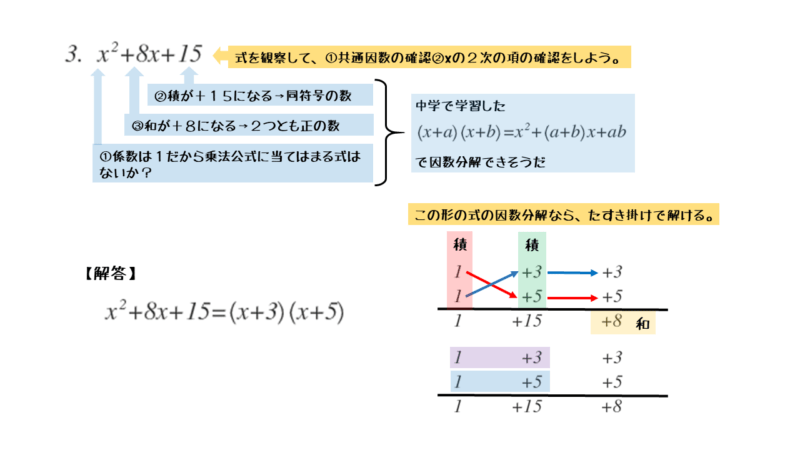
\begin{align*} \quad x^2 +8x+15 \end{align*}式をよく観察すると、以下のことが分かります。
与式をよく観察しよう
- x2,+8x,+15の3項からなる多項式
- 文字xについての2次式
- 2次の項の係数は1
- 各項に共通因数は見当たらない。
与式は問2と同じ形の式です。ですから、問2と同じ流れで因数分解できます。
定数項+15(積)の因数の組み合わせを考え、その組み合わせが正しいかを1次の項+8xの係数+8(和)で確かめます。積が+15で和が+8になる数の組合せは、+3と+5です。
数の組合せが分かったので、与式を因数分解します。
問3の解答例
積が $15$、和が $8$ となる数の組合せから
\begin{align*} \quad x^2 +8x+15 =\left(x+3 \right)\left(x+5 \right) \end{align*}たすき掛けでも因数分解できます。ただし、2次の係数が1であれば、これまで通りの因数分解で良いでしょう。
たすき掛けは、2次の項の係数が1でも利用できる。
問3のポイントと解答例をまとめると以下のようになります。
問4の解答・解説
問4
次の式を因数分解せよ。
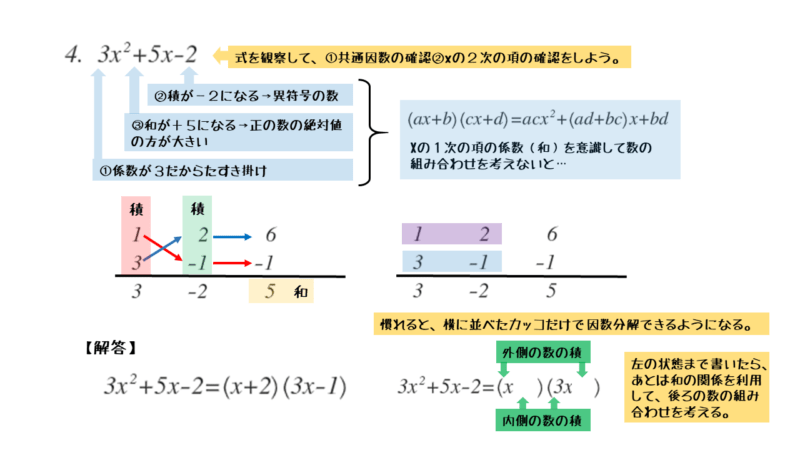
\begin{align*} \quad 3x^2 +5x-2 \end{align*}式をよく観察すると、以下のことが分かります。
与式をよく観察しよう
- 3x2,+5x,-2の3項からなる多項式
- 文字xについての2次式
- 2次の項の係数は3
- 各項に共通因数は見当たらない。
xについての2次式で、2次の項の係数が1でなければ、たすき掛けによる因数分解です。基本的に3項からなる2次式であれば、たすき掛けによる因数分解を考えましょう。
たすき掛けによる因数分解は、2次の項の係数と定数項のそれぞれで因数(数の組合せ)を考えるのがポイントです。定数項の方は、1次の項を参考にしながら符号も考慮に入れます。
2次の項の係数は3なので、数の組合せは1と3です。また、定数項は-2なので、数の組合せは、1と-2または-1と2です。
因数の組合せが複数組あっても、気にする必要はありません。たすき掛けをして、1次の項の係数と比較して同じになったものが正しい因数の組合せです。
1次の項の係数が+5であることを考慮すれば、定数項における数の組合せは-1と2の方が良さそうです。慣れてくれば、ある程度は暗算できるようになります。
たすき掛けをして(下図参照)、1次の項の係数に等しくなることが確認できれば、与式を因数分解します。
問4の解答例
与式をたすき掛けで因数分解すると
\begin{align*} \quad 3x^2 +5x-2 =\left(x+2 \right)\left(3x-1 \right) \end{align*}問4のポイントと解答例をまとめると以下のようになります。
なお、図解の方で解説していますが、展開と因数分解の関係が分かってくると、たすき掛けなしで因数分解できるようになります。コツを掴んでしまえば暗算でできるようになるので、ぜひ、挑戦してみましょう。
問5の解答・解説
問5
次の式を因数分解せよ。
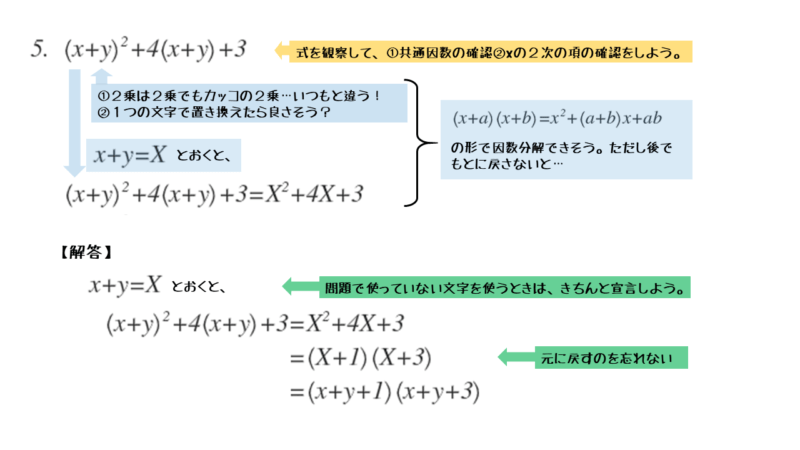
\begin{align*} \quad \left(x+y \right)^2 +4\left(x+y \right)+3 \end{align*}式をよく観察すると、以下のことが分かります。
与式をよく観察しよう
- (x+y)2,+4(x+y),+3の3項からなる多項式
- 1,2番目の項に、共通の多項式(x+y)がある
- 多項式(x+y)を1つのかたまりと考えると、与式は(x+y)についての2次式
問5では、多項式(x+y)を1つのかたまり(1つの文字)と捉えられるかがポイントです。慣れていないと、展開したくなるかもしれません。
多項式(x+y)を1つの文字に置き換えてみると、与式が全く違った式に見えてきます。
たとえば、多項式(x+y)を文字Xに置き換えてみると、与式は文字Xについての2次式になります。
問5の解答例 1⃣
\begin{align*} \quad x+y=X \end{align*}とおくと、与式は
\begin{align*} \quad &\left(x+y \right)^2 +4\left(x+y \right)+3 \\[ 7pt ] = \ &X^2 +4X+3 \end{align*}置き換えた後の式であれば、問2,3と同じようにして因数分解できます。
問5の解答例 2⃣
\begin{align*} \quad &\vdots \\[ 7pt ] &\left(x+y \right)^2 +4\left( x+y \right)+3 \\[ 7pt ] = \ &X^{\scriptsize{2}}+4X+3 \end{align*}これを因数分解すると
\begin{align*} \quad &X^{\scriptsize{2}}+4X+3 \\[ 7pt ] = \ &\left(X+1 \right)\left(X+3 \right) \end{align*}ここで
\begin{align*} \quad X=x+y \end{align*}であるので、与式を因数分解すると
\begin{align*} \quad &\left(x+y \right)^2 +4\left(x+y \right)+3 \\[ 7pt ] = \ &\left(x+y+1 \right)\left(x+y+3 \right) \end{align*}因数分解した後に注意したいのは、もとの多項式(x+y)に戻すことです。少し工夫の必要な因数分解ですが、難易度の高い問題というわけではありません。
問5のポイントと解答例をまとめると以下のようになります。
与式に使われている文字で、因数分解の方針が分かるかも
演習をこなしていくと、与式の形はもちろんですが、与式で使われている文字でも、因数分解の方針をある程度予測できるようになります。
たとえば、文字x,yを使った式の因数分解であれば、ほとんどが乗法公式による因数分解とたすき掛けによる因数分解のどちらかです。
また、文字a,b,cを使った式の因数分解であれば、ほとんどが分配法則の逆による因数分解(輪環の順に整理するタイプ)です。
絶対ではありませんが、与式に使われている文字に注目しながら演習してみると、それほど外れていないことが分かると思います。目安程度かもしれませんが、知っておいて損はないでしょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 因数分解のパターンは、分配法則の逆による因数分解と、乗法公式による因数分解の2パターン。
- 分配法則の逆による因数分解では、共通因数を見つける。
- 乗法公式を利用した因数分解では、どの乗法公式に当てはまるかを考える。
- 3項からなる2次式であれば、基本的にたすき掛けを利用した因数分解。