数と式|整式の因数分解について

今回は、整式の展開と関係の深い整式の因数分解です。
展開と因数分解の関係は、互いに逆の操作になります。ですからセットで学習するのが効率的です。
因数分解の定義
因数分解とは、数や多項式などを積の形で表すことです。
積の方で表したとき、掛け合わせる1つ1つを因数と言います。数や式を因数に分解するので、因数分解と言います。
たとえば、15という数を因数分解すれば、3×5という積で表すことができます。この3,5を15の因数と言います。もちろん、1×15という積でも表すこともできるので、1,15も15の因数です。
因数分解
\begin{align*} \quad 15 &= 1 \times 15 \\[ 7pt ] &= 3 \times 5 \end{align*}より、$1 \ , \ 3 \ , \ 5 \ , \ 15$ は $15$ の因数
因数はもとの数や式を構成する部品と考えれば良い。因数分解は、構成する部品の分かる形(=積の形)で表すこと。
単項式の因数分解
単項式と言っても、数だけのものや文字を含むものがあります。
数の因数分解
単項式のうち、数だけのものを因数分解してみます。
たとえば、6を因数分解します。負の数を使っても積の形で表せますが、今回は省略します。
6の因数分解
\begin{align*} \quad 6 &= 1 \times 6 \\[ 7pt ] &= 2 \times 3 \end{align*}より、$1 \ , \ 2 \ , \ 3 \ , \ 6$ は $6$ の因数
因数を見てみると、6の約数であることが分かります。数を因数分解するとき、もとの数の約数を考えると因数を探しやすくなります。
数の因数分解では、約数を考えよう。
文字を含む単項式の因数分解
単項式のうち、文字を含むものを因数分解してみます。
たとえば、単項式2aを因数分解します。文字を含む単項式では乗算の計算記号を補うと、因数を知ることができます。
2aの因数分解
\begin{align*} \quad 2a = 2 \times a \end{align*}ここで
\begin{align*} \quad 2a = 1 \times 2a \end{align*}と因数分解することはできない。
よって、$2 \ , \ a$ は $2a$ の因数
単項式は、もともと数や文字の積で表され、乗算の計算記号を省略した式です。
文字を含む単項式では、数と文字とで分けると、それらが因数。
多項式の因数分解
多項式の因数分解であっても、積で表すことに変わりはありません。多項式をいくつかの数や式の積で表すためには、展開の知識が必要になります。
展開は、数や式の積を単項式の和で表すことです。ですから、展開する前の状態に戻せば、数や式の積で表すことができるはずです。
因数分解には様々な解釈の仕方があります。
因数分解とは
- 展開する前の状態に戻す作業(展開と逆の操作)
- 式を和の形から積の形に変形する作業
- 式をカッコなしの状態からカッコありの状態に変形する作業
展開前の式に戻せば、乗算する数や式が因数になります。特に、多項式の因数分解では、因数には多項式が含まれるので注意が必要です。
展開のやり方が分配法則だけであるのに対して、因数分解のやり方は与式によって異なります。そういう意味では、展開よりも因数分解の方が難しさを感じるかもしれません。
因数分解の典型的なパターンを2つ取り上げるので、それらをきちんとマスターしておきましょう。
展開のやり方は2パターン
展開の本質は分配法則なので、基本的には分配法則による展開です。ただし、特定の式に当てはまると、乗法公式による展開があります。
分配法則による展開と、乗法公式による展開に違いが出るとすれば、展開後の項数です。これは、どちらの方法で展開したかを判断する材料になります。
たとえば、2項式どうしの積を展開するとします。乗法公式に当てはまらなければ、分配法則で展開するしかありません。
分配法則を2セット行うと、4つの項ができます。同類項がなければ、項数は4つのままです。
それに対して、乗法公式による展開であれば、同類項を整理した後の式で展開できるので、3つ、または2つの項になることがあります。
分配法則による展開と乗法公式による展開
分配法則による展開
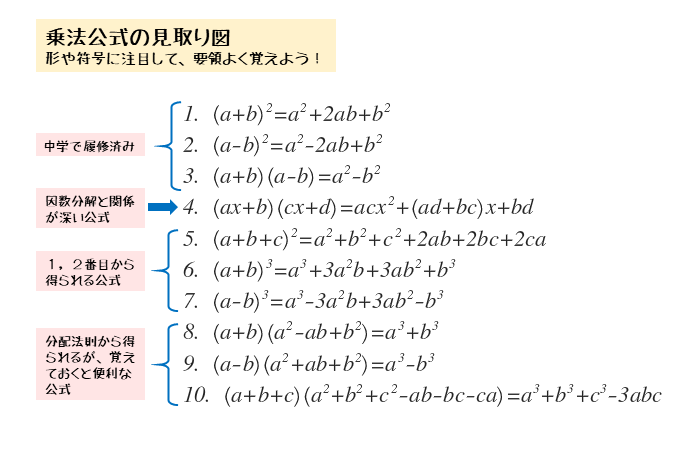
\begin{align*} \quad \left(a+b \right)\left(c+d \right)=ac+ad+bc+bd \end{align*}乗法公式による展開
\begin{align*} \quad \left(a+b \right)^{2}=a^{2}+2ab+b^{2} \end{align*}要するに、乗法公式による展開は、分配法則で展開しただけでなく、同類項の整理までを含めた形で展開できます。
乗法公式で展開=分配法則で展開+同類項の整理
これを踏まえて展開を分類すると、主に2パターンに分類できます。
項数で分類した展開
- 乗法公式に当てはまらず、分配法則で展開した場合
- 乗法公式に当てはまり、公式に当てはめて展開した場合
乗法公式に当てはまらず、分配法則で展開した場合
単項式と多項式の積を分配法則で展開した場合
乗法公式に当てはまらず、分配法則で展開するのは、ほとんどが単項式と多項式の積を展開する場合です。
単項式と多項式の積を分配法則で展開するときを考えます。単項式をカッコ内の多項式に乗算して展開します。
分配法則による展開
\begin{align*} \quad a\left(b+c \right) \end{align*}を展開すると
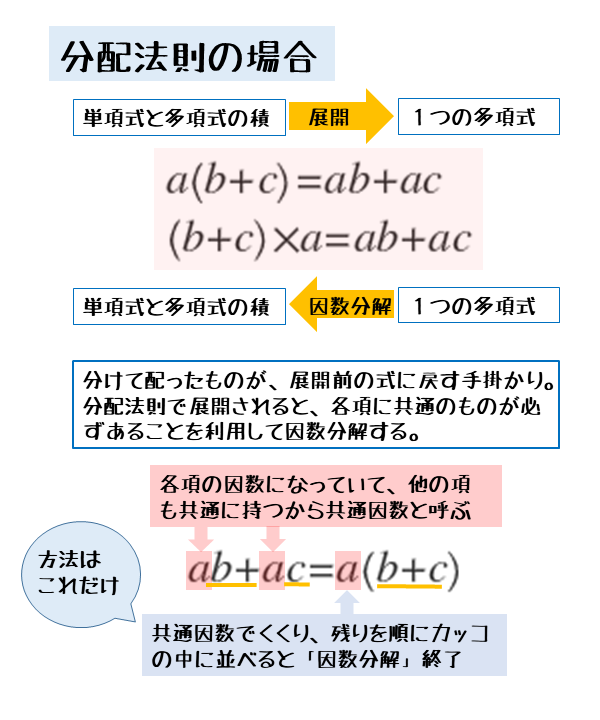
\begin{align*} \quad a\left(b+c \right)=\underline{a} \times b+\underline{a} \times c \end{align*}展開後の式を見ると、各項にはaが共通に存在します。共通に存在するaは、各項における因数です。
このように、各項に共通して存在し、各項において因数であるものを共通因数と言います。乗法公式に当てはまらず、分配法則で展開した後の式には、共通因数が必ず存在します。
分配法則による因数分解
\begin{align*} \quad ab+ac \end{align*}を因数分解すると
\begin{align*} \quad \underline{a} b+\underline{a} c= \underline{a} \left(b+c \right) \end{align*}共通因数があれば、展開するときにそれを各項に分配したと考えます。そして、分配法則を使う前の式に戻すと、因数分解することができます。
戻し方は手順通りにやれば簡単です。
分配法則による展開式を因数分解する手順
- 共通因数aを先頭に置く。
- 共通因数aの後ろにカッコを書く。
- カッコの中に、共通因数aを除いた部分b+cをそのまま書く。
なお、各項から共通因数を取り出すことを、一般に共通因数でくくると言います。
このパターンの因数分解では、共通因数を見つけることがポイントです。また、共通因数による因数分解は、最優先のパターンなので、必ずマスターしておきましょう。
多項式どうしの積を分配法則で展開した場合
多項式どうしの積を分配法則で展開した場合、先ほどと少し様子が異なります。
多項式のどうしの積を分配法則で展開した場合、分配法則を2セット行っています。展開の様子を良く観察すると、前の多項式の各項を、後ろの多項式に乗算しています。
分配法則による展開
\begin{align*} \quad \left(a+b \right)\left(c+d \right) \end{align*}を展開すると
\begin{align*} \quad &\left(a+b \right)\left(c+d \right) \\[ 7pt ] = \ &\underline{a} \times \left(c+d \right)+\underline{\underline{b}} \times \left(c+d \right) \\[ 7pt ] = \ &\underline{a}c+\underline{a}d+\underline{\underline{b}}c+\underline{\underline{b}}d \end{align*}この場合、展開後の式には2種類の共通因数が存在することになります。式全体で共通因数が存在しないのが特徴です。
そこで同じ共通因数を持つ項だけでそれぞれ因数分解をします。すると、新たな共通因数が現れます。
分配法則による因数分解
\begin{align*} \quad ac+ad+bc+bd \end{align*}を因数分解すると
\begin{align*} \quad &\underline{a}c+\underline{a}d+\underline{\underline{b}}c+\underline{\underline{b}}d \\[ 7pt ] = \ &a \underline{\left(c+d \right)}+b \underline{\left(c+d \right)} \\[ 7pt ] = \ &\underline{\left(c+d \right)}\left(a+b \right) \\[ 7pt ] = \ &\left(a+b \right)\left(c+d \right) \end{align*}新たな共通因数でくくると、因数分解の終了です。このように共通因数でくくる作業を2セット行うことで、与式を因数分解することができます。
展開の計算過程を逆に戻っているだけなので、難しく考える必要はありません。分配法則を2セット行って展開したので、それと逆の作業である因数分解も2セット行います。
展開するときの計算過程を省略せずに書き、それを答えの方から辿ってみよう。計算の仕組みを理解するために、計算過程を丁寧に書く習慣を。
次からが高校数学でよく出てくる因数分解になります。
乗法公式に当てはまり、公式で展開した場合
乗法公式に当てはめて展開した後の式は、同類項を整理した後の式です。ですから、分配法則による展開と比べて項数が異なります。
しかも共通因数がないので、分配法則の性質を利用しても上手く因数分解できません。ですから、共通因数による因数分解と切り離して考えなければなりません。
乗法公式で展開した式を因数分解する場合、文字xの1次式どうしの積を展開する乗法公式(4番目)に関する因数分解が重要です。
文字xの1次式どうしの積に因数分解するときはたすき掛けを利用
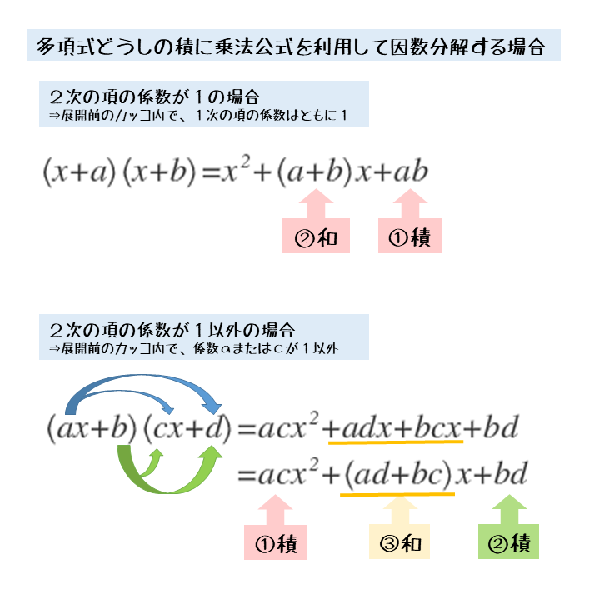
文字xの1次式どうしの積を展開すると、3項式になります。3つの項は、文字xの2次の項、文字xの1次の項、定数項です。
文字xの1次式どうしの積の展開は、中学でも学習しています。中学と異なるのは、文字xについて2次の項の係数が1 以外になる場合もあることです。
展開後の式で、2次の項の係数が1であれば、定数項の因数を考えるだけで因数分解できます。それに対して、2次の項の係数が1以外であれば、定数項の因数を考えるだけでは上手くいきません。
その理由は、1次の項の係数が定数項の因数の和にならないからです。
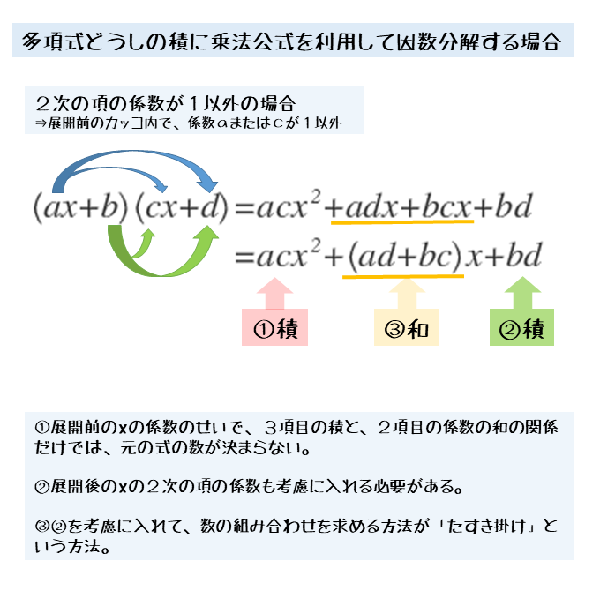
このような式を因数分解するときに利用するのが、「たすき掛け」という方法です。斜めに乗算することからその名前で呼ばれます。
たすき掛けは、定数項だけでなく、2次の項の係数も考慮しており、しかも因数分解を機械的に行うことができる方法です。
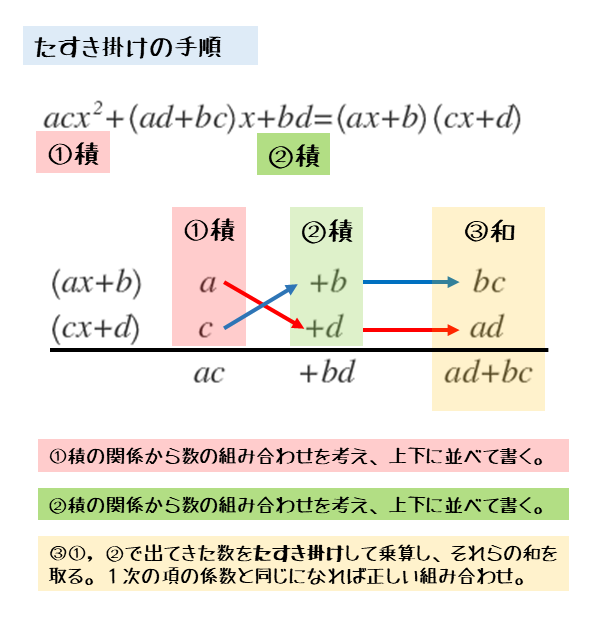
たすき掛けの手順を図解すると以下のようになります。
2次の項の係数と定数項から、因数の組み合わせを考えます。組み合わせをそれぞれ縦に並べ、たすき掛け(=斜め)に乗算します。たすき掛けに乗算するのは、分配法則が原因です(同じカッコ内の項と乗算しないから)。
乗算した後の2数の和は、1次の項の係数です。この和を与式の係数と比べることで、因数の組み合わせが正しいか分かります。
因数の組み合わせは、2次の項の係数についてはたいてい1通りで済みます。しかし、定数項については因数の組み合わせが複数になることが多いです。
もし、因数の組み合わせが間違っていれば、1次の項の係数と同じ数になりません。この場合、別の組み合わせを考える必要があります。