数と式|整式の因数分解について

たすき掛けを利用して因数分解してみよう
次の式を因数分解してみましょう。
例題
次の式を因数分解せよ。
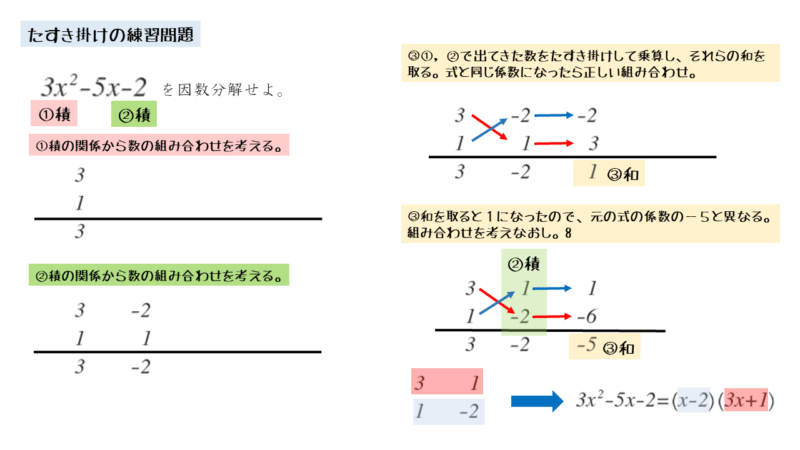
\begin{align*} \quad 3x^2 -5x-2 \end{align*}例題の式は、文字xについての2次式です。3項式なので、たすき掛けを使う典型的な式です。
まず、2次の項の係数から因数の組み合わせを考えます。
係数が3なので、因数の組み合わせは1,3の1通りです。負の数の組み合わせは考えません。
次に、定数項から因数の組み合わせを考えます。
定数項の因数には、負の数も候補に入れる必要があります。定数項がー2なので、因数の組み合わせは、-1,2と1,-2の2通りあります。
因数の組み合わせが決まったら、たすき掛けの手順通りに因数をそれぞれ縦に並べます。
因数の候補が複数考えられる場合、とりあえず思いついたもので良いのでたすき掛けを行いましょう。もちろん、正解の組み合わせでない場合もあります。
しかし、焦らずに組み合わせを変えてたすき掛けしましょう。経験がものを言いますが、慣れないうちはあまり気にする必要はありません。
同じ因数の組み合わせでも、並べ方によって上手くいかないことが分かります。組合せはそのままで上下に入れ替えると上手くいっています。
入れ替えただけですが、乗算する相手が変わったので、1次の項の係数も異なる数になりました。このように因数を上下で入れ替えると異なる結果になるので、別の組み合わせと考えます。
1次の項の係数と同じになれば、正解の組み合わせです。
因数の組み合わせを変えるのは、基本的に定数項の方。上下逆にしたり、符号を付け変えたりして、たすき掛けを繰り返そう。どうしても上手くいかない場合、2次の項の係数の方を変えてみよう。
たすき掛けが上手くいけば、カッコ内の数の組み合わせや並びが決まったということです。横に並んだ数が同じカッコ内の数です。このとき文字xを忘れずに書きましょう。これがたすき掛けによる因数分解です。
演習次第で、正しい因数の組み合わせが分かったり、たすき掛けなしで因数分解できたりします。たくさん演習をこなしましょう。
高校数学での因数分解と言えば、たすき掛けによる因数分解がメインです。たすき掛けの仕組みをしっかり理解しましょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 因数分解は、展開の逆の操作。
- 因数分解をするときは、まず共通因数を探そう。
- 共通因数があれば、分配法則の逆で因数分解。
- 共通因数がなければ、乗法公式を利用して因数分解。
- 3項からなる文字xの2次式を見たら、たすき掛けによる因数分解を考えよう。