数と式｜不等式について

07/17/2021数学１

今回は「一次不等式」について学習します。その中でも基本となる不等式の扱い方についてです。

不等式の扱い方は基本的に等式の扱い方と変わりません。ですから、等式の扱いと違う点に注目すると覚えやすいです。

1. 大小関係のある式が不等式
2. 不等式の記号は４種類
3. 不等式の性質
4. Recommended books
- 4.1. オススメその１
- 4.2. オススメその２
5. さいごに、もう一度まとめ

大小関係のある式が不等式

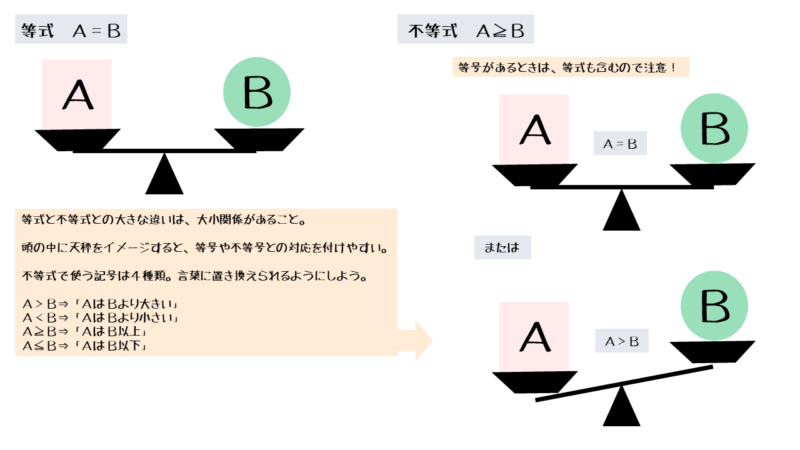
等式は２つの数量が等しいことを表す式です。それに対して、不等式は２つの数量が等しいときもありますが、基本的には２つの数量に大小関係があることを表す式です。

等式や不等式を見たとき、天秤の様子を思い浮かべると２つの数量の関係をイメージしやすい。

不等式の記号は４種類

不等式に使われ、大小関係を表す記号のことを不等号と言います。不等号には、単純な大小関係を表す＞（大なり）、＜（小なり）と、等号の付いた≧（大なりイコール)、≦（小なりイコール）の４種類があります。

不等式を扱うとき、式を言葉に置き換えて考えると、大小関係を間違わずに済みます。

不等式を言葉に置き換えて考える

ａ＞ｂは、「ａ大なりｂ」または「ａはｂより大きい」
ａ＜ｂは、「ａ小なりｂ」または「ａはｂより小さい」
ａ≧ｂは、「ａ大なりイコールｂ」または「ａはｂ以上」
ａ≦ｂは、「ａ小なりイコールｂ」または「ａはｂ以下」

等式と同じように、不等号の左側を左辺、右側を右辺と言います。以上、以下などは、左辺と右辺に大小関係があるとき、または左辺と右辺が等しいときであるので注意が必要です。

「大＞小」「小＜大」と覚えよう。「大は小より大きい」や「小は大より小さい」のように、左から素直に読んだ言い回しの方が間違わずに済む。

不等式の性質

等式の性質と同じように、不等式にもいくつか性質があります。この性質を利用して、不等式を変形することができます。

基本的には等式の性質と同じですが、異なるのは負の数がかかわるときです。

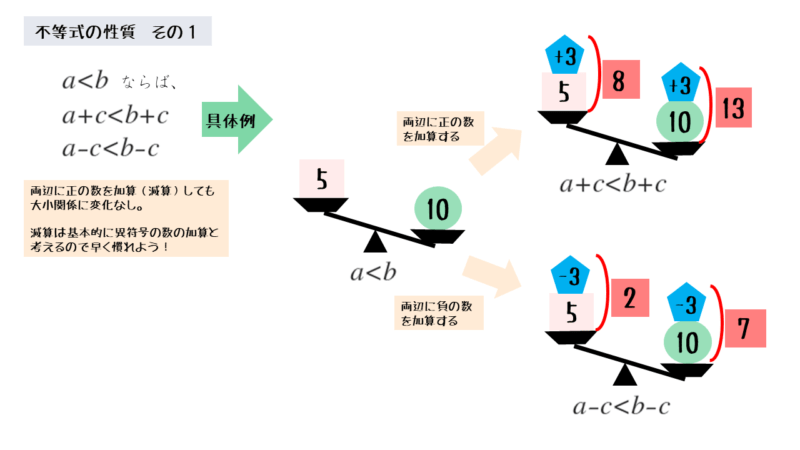
両辺に正負の数を加算しても不等式は成り立つ

等式の性質では減算も扱いますが、減算は負の数の加算と考えると、不等式では１つの性質で説明できます。マイナスの符号を見て、減算と間違わないようにしましょう。

具体的な数を使うとこの性質が成り立つことが分かります。この性質は、等式と同じように移項が成り立つ根拠になります。

移項の仕組み

\begin{align*} a + b &\gt c +d \\[ 7pt ] a + b + \underline{\left( -b \right)} &\gt c + d + \underline{\left( -b \right)} \\[ 7pt ] a &\gt c + d -b \end{align*}

両辺に(－ｂ)を加算して左辺を整理すると、もともと左辺にある項＋ｂが右辺に移動したように見えます。このことから「移項」と呼んでいます。

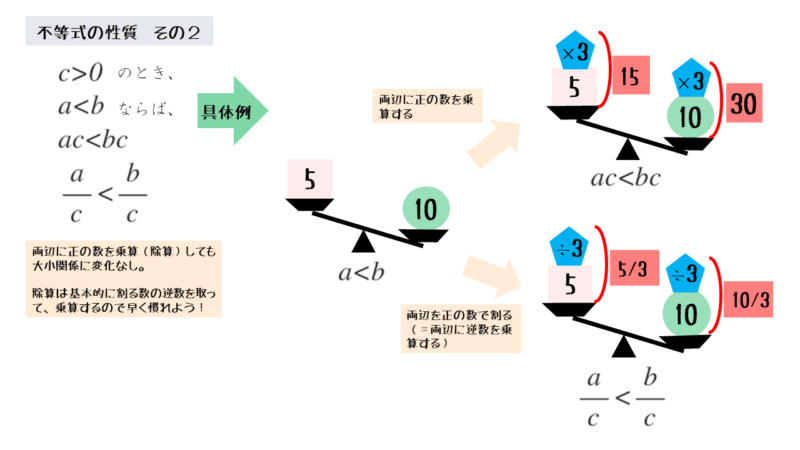
両辺に正の数を乗算しても不等式は成り立つ

等式の性質では除算も扱いますが、除算は逆数の乗算と考えると、不等式では１つの性質で説明できます。

具体的な数を使うと、この性質も成り立つことが分かります。この性質は、等式と同じように式変形の最後でよく用いられる性質です。

不等式の両辺に正の数を乗算する

\begin{align*} &\text{不等式} \\[ 5pt ] &\quad 10 \gt -5 \\[ 7pt ] &\text{の両辺に $3$ を掛けると} \\[ 5pt ] &\quad \text{（左辺）} =10 \times 3 =30 \\[ 7pt ] &\quad \text{（右辺）} =-5 \times 3 =-15 \\[ 7pt ] &\text{より} \\[ 5pt ] &\quad 30 \gt -15 \end{align*}

不等式の両辺に正の数を乗算すると、不等号の向きが変わっていないことが分かります。このことから、不等式が成り立つと言えます。

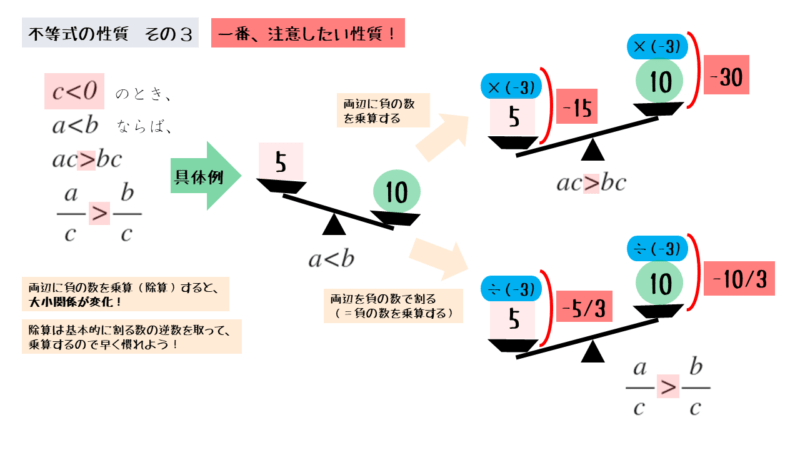
両辺を負の数で乗算すると、大小関係が変化する

等式では２つの数量が等しい関係だったので、両辺に対して同じ処理をすれば、２つの数量の関係が変わることはありません。

しかし、不等式では、負の数を乗算すると２つの数量の大小関係が変化します。

両辺に負の数を乗算すると、数量が正の数から負の数へ、または負の数から正の数へと変わります。両辺の正負が逆転することによって、大小関係も逆転してしまいます。これは除算でも同じです。

不等式の両辺に負の数を乗算する

\begin{align*} &\text{不等式} \\[ 5pt ] &\quad 10 \gt -5 \\[ 7pt ] &\text{の両辺に $-3$ を掛けると} \\[ 5pt ] &\quad \text{（左辺）} =10 \times \left(-3 \right) =-30 \\[ 7pt ] &\quad \text{（右辺）} =-5 \times \left(-3 \right) =15 \\[ 7pt ] &\text{より} \\[ 5pt ] &\quad -30 \lt 15 \end{align*}

不等式の両辺に負の数を乗算すると、不等号の向きが変わっていることが分かります。このことから、不等式が成り立たないと言えます。

両辺に負の数を乗除算すると、不等号の向きは逆になる。

この性質も式変形に用いられますが、不等式の性質の中で特に間違いやすい性質です。符号の付け忘れはもちろんですが、不等号の向きを変え忘れることが多いので注意しましょう。