数と式|数の定義について

高校数学で扱う数とその定義について学習しましょう。
高校数学で扱う数の範囲は、中学までと比べて広くなります。整数が出てきたらラッキーくらいに考えておいた方が良いかもしれません。
初めのうちは「~の範囲で答えなさい」と言った親切な問題もありますが、このような但し書きもそのうちなくなります。高校数学で扱う数にできるだけ早く慣れましょう。
高校数学で扱う数の分類
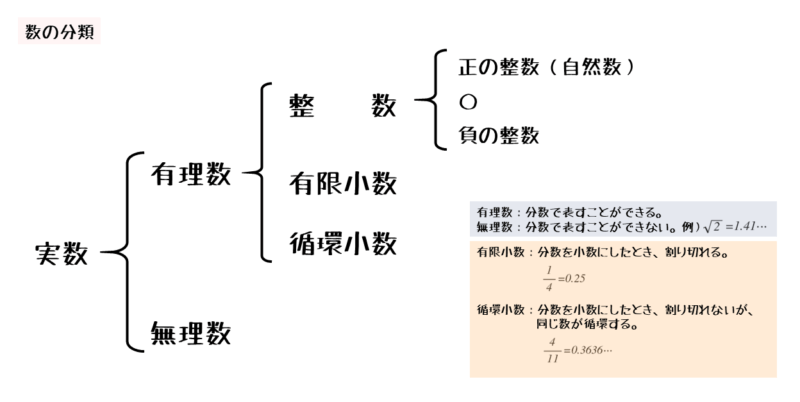
高校で扱う数を分類すると、以下のようになります。
高校で扱う数は、実数の範囲にある数を対象としています。中学までで扱っていた数は、実数、あるいは有理数の一部になります。これまで扱ってきた数に加えて、他の数についての知識が増えます。
有理数と無理数が対の関係になっていたり、有理数には整数、有限小数、無限小数などがあったりなどと、それぞれの数で属する範囲があります。
自分の扱う数がどんな数かを分かって使えるようになりましょう。
実数の定義
実数とは、実体があり、実際に測ることのできる数のことです。普段から四則計算で扱っている数のことなので、特に難しく考える必要はありません。
また、実数は有理数と無理数の総称でもあります。
ちなみに実数と対になり、実体のない数は虚数。虚数は「複素数」の単元で学習する。
有理数と無理数の定義とその違い
有理数と無理数は、ともに実数の範囲にある数で、その違いは分数で表せるかどうかです。
有理数は分数で表すことができますが、無理数は分数で表すことができません。
有理数
分数で表せる有理数は、整数、循環小数、有限小数の3種類に分類できます。
整数は基本的に分数で表しませんが、計算などでは分数で表すこともあります。ですから、整数は有理数の定義に当てはまる数です。
また、有限小数は、名前の通り有限な小数で、小数点以下に必ず終わりがある小数です。
有限小数に対して、循環小数は、小数点以下が無限に続き、小数点以下に同じ数字の繰り返しが現れる小数です。
数字が循環しても、無限に続くのであれば、分数で表せないような気がします。しかし、きちんと分数で表すことができます。
有理数は分数で表せる数。特に循環小数を分数で表す問題は頻出なので、演習をこなしておこう。
無理数
無理数は、有理数と同じ実数に分類され、有理数と対になる数です。無理数は有理数と異なり、分数で表すことができない数です。
中学で学習した平方根は無理数です。この平方根は、小数点以下が無限に続き、しかも循環しない小数です。
無限小数を記述するのは大変です。それを解消するために、平方根であれば根号(ルート)という記号を使って表します。
このような無限小数は、循環小数と異なり、分数で表すことができません。
有理数と無理数の定義をセットで覚えよう。分数で表せるかどうかが分類のポイント。
循環小数の扱い
数を扱った問題で多いのが、循環小数の表し方や分数への変換です。循環小数は無限小数ですが、有理数なので分数で表すことができます。
循環小数の表し方
循環小数は小数点以下が無限に続く数なので、ある規則に従って小数点以下を工夫して表します。毎回、小数点以下を長々と記述するのは面倒だからです。
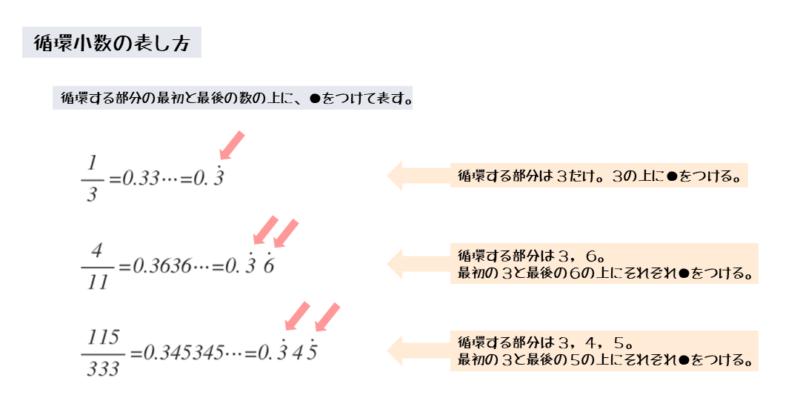
規則と言うほどのものではありません。循環する数字が分かるように、数字の上に黒丸を付けるという規則です。
循環する数字の桁数によって、黒丸の付け方が少し変わります。
循環小数の表し方
- 小数点以下で、循環する数字が1桁のとき、その数字の上に黒丸を付ける。
- 小数点以下で、循環する数字が2桁のとき、2つの数字の上に黒丸を付ける。
- 小数点以下で、循環する数字が3桁のとき、1桁目と3桁目の数字の上に黒丸を付ける。
黒丸の数は、循環する数字の桁数によって異なります。
循環する数字の桁数が3桁以上になると、黒丸を付けるのは最初と最後の数字の2箇所だけで構いません。おそらく、黒丸を付けすぎると、逆に分かりにくくなるからかもしれません。
循環小数を分数で表す
分数を小数で表したり、有限小数を分数で表したりすのは、難しくありません。
しかし、循環小数は無限に続く小数です。そうなると、有限小数と同じように10や100などを分母にした分数で表せそうにありません。
「循環小数を分数で表せ」という問題を解くためには、分数で表すための方法を知っていることが絶対です。知らなければまず解けないだろうと思います。
循環小数を分数で表してみよう
次の循環小数を分数で表してみましょう。
例題
$2.\dot{1}\dot{5}$ を分数で表せ。
例題の解答・解説
循環小数の最大の特徴は、小数点以下に同じ数字の並びが繰り返し現れることです。この性質を利用します。
まず、循環小数を用いて等式を作ります。
例題の解答例 1⃣
\begin{align*} \quad x=2.\dot{1}\dot{5} \quad \cdots \text{①} \end{align*}とおく。
この等式だけでは循環小数を分数で表すことができません。
ところで、与えられた循環小数は、小数点以下の1,5の2桁が繰り返し現れる数です。
循環小数の循環部分に注目する
\begin{align*} \quad x=2. \underline{15151515 \cdots \cdots } \end{align*}分数で表せないのは、循環小数だからです。循環小数が有限小数になれば、分数で表すことができます。
一番手っ取り早いのは、原因となっている循環部分がなくなることです。等式①を作ったのは、小数点以下の循環する部分をなくす処理を行うためです。
ただし、等式①だけでは難しいので、新しい等式を導きます。新たに導く等式は、たとえば、両辺を100倍するなどした式です。
例題の解答例 2⃣
\begin{align*} \quad x &=2.\dot{1}\dot{5} \quad \cdots \text{①} \\[ 7pt ] &\vdots \end{align*}①の両辺に $100$ を掛けて
\begin{align*} \quad 100x=215.\dot{1}\dot{5} \quad \cdots \text{②} \end{align*}等式①の両辺を100倍すると、等式②を導くことができます。
等式②の右辺を見ると、循環小数の小数点がもとの位置から右に2つずれます。このとき、小数点以下の数字の並びは、もとの数と同じように1,5が循環します。
この2つの等式を減算すると、循環部分が消えて無くなります。
例題の解答例 3⃣
\begin{align*} \quad x &=2.\dot{1}\dot{5} \quad \cdots \text{①} \\[ 7pt ] &\vdots \\[ 7pt ] 100x &=215.\dot{1}\dot{5} \quad \cdots \text{②} \end{align*}②-①
\begin{align*} \quad 99x=213 \end{align*}減算した後、xについて解きます。xはもとの循環小数のことです(等式①より)。
例題の解答例 3⃣
\begin{align*} \quad x &=2.\dot{1}\dot{5} \quad \cdots \text{①} \\[ 7pt ] &\vdots \\[ 7pt ] 99x &=213 \end{align*}これを $x$ について解くと
\begin{align*} \quad x=\frac{213}{99}=\frac{71}{33} \end{align*}よって
\begin{align*} \quad 2.\dot{1}\dot{5}=\frac{71}{33} \end{align*}循環部分を消去することで、無限小数を有限小数にすることができます。ここがポイントです。そのためには、始めに等式を作ることが必要です。
10倍か100倍かは循環部分の桁数で決める
等式の両辺を何倍するかは、循環する数字の桁数で決まります。循環部分がきれいに消えるように、10や100などを両辺に掛けましょう。
循環する数字の桁数に応じて、両辺に10や100を掛けよう。
例題のポイントと解答例をまとめると以下のようになります。
この解法は知ってしまえば大したものではありませんが、有限小数や循環小数の性質を利用した上手い方法です。また、約分をすることが多いので、分数を作って終わりにしないように気をつけましょう。
Recommended books
オススメその1
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学1・Aでは2冊とも中学で学習した内容にも触れており、中学内容と高校内容とのつながりを把握しやすい教材です。
一学期のうちは不安を抱えながら学習を進めていく人も多いかと思います。スタートで躓かないためにも易しく取り組みやすい教材を使うのも一つのやり方です。無理をして内容の難しい教材を使うよりもはるかに良いでしょう。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学1・A 改訂版 その1』は「数と式」「2次関数」の単元を扱っています。
『高校とってもやさしい数学1・A 改訂版 その2』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
オススメその2
『高校の数学I・Aが1冊でしっかりわかる本』は、これ1冊で数学1・Aの全範囲を復習できます。内容のレベルは「とってもやさしい」シリーズとそれほど変わらず、教科書レベルです。
本書と「とってもやさしい」シリーズのページ数を比較してみました。「とってもやさしい」シリーズは、1冊ごとのページ数が少ないのですが、分冊なのが難点です。
- 高校とってもやさしい数学1・A 改訂版 その1:175ページ
- 高校とってもやさしい数学1・A 改訂版 その2:189ページ
- 高校の数学I・Aが1冊でしっかりわかる本:192ページ
ページ数を比べると分かるように、本書の方が1冊でも遥かにページ数が少ないので、短時間でこなすことができます。
紹介した教材を使うとした場合、高校1年生であれば「とってもやさしい」シリーズで復習し、高校2,3年生であれば『高校の数学I・Aが1冊でしっかりわかる本』と「とってもやさしい」シリーズを組み合わせて復習すると良いでしょう。
こんな人に向いています
- 定期試験や大学受験のための基礎を固めて、成績を上げたい高校生へ。
- 医療看護系入試、高卒認定試験などの対策で、短期間で数学1・Aを理解したい方へ。
- 学び直しや頭の体操をしたい大人の方へ。
さいごに、もう一度まとめ
- 実数は、今まで扱ってきた数の総称。
- 有理数と無理数は実数に属し、分数で表せるかどうかで決まる数。
- 整数、有限小数、循環小数は有理数に属し、分数で表せる数。
- 循環小数は、黒丸を使うと簡略化して表せる。
- 循環小数を分数で表すとき、循環部分を消去して有限小数にする。