集合と論理｜逆、裏、対偶について
今回は、逆、裏、対偶について学習しましょう。命題を色んな視点から扱います。
物事を一方向だけから見ることに慣れてしまうと、独りよがりな結論になってしまうことがあります。そのことに気付けないと、取り返しのつかない失敗をするかもしれません。
それを防ぐためには、様々な角度から検証したり、論理的に思考したりする客観性を身に付ける必要があります。数学Ａでは、そのような能力を身に付けるきっかけとなる分野ではないかと思います。
記事の画像が見辛いときはクリックすると拡大できます。
ある命題の逆、裏、対偶
ある命題「ｐ⇒ｑ」の真偽を調べるとき、真偽の判定がどうしても難しいことがあります。
そのようなとき、命題の逆、裏、対偶を利用すると、命題の真偽を簡単に判定できることがあります。
もとの命題とその逆、裏、対偶とがどのような関係があるかを知りましょう。
命題の逆、裏、対偶の定義
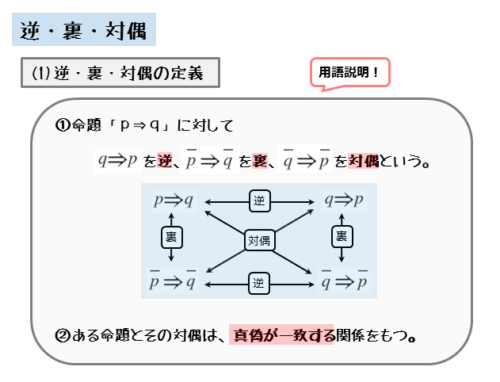
命題の逆とは、命題「ｐ⇒ｑ」において、仮定と結論を入れ替えた「ｑ⇒ｐ」のことです。
また、命題の裏とは、命題「ｐ⇒ｑ」において、仮定と結論を否定した「ｐの否定⇒ｑの否定」のことです。
さらに、命題の対偶とは、命題「ｐ⇒ｑ」において、命題の逆の裏、または命題の裏の逆となる「ｑの否定⇒ｐの否定」のことです。
ちなみに、命題の逆「ｑ⇒ｐ」は、命題の裏「ｐの否定⇒ｑの否定」から見れば、逆の裏、または裏の逆となるので、これらは対偶の関係にあります。
詳細は後述しますが、逆、裏、対偶のうち、もとの命題の真偽と必ず一致するのは対偶だけです。
命題とその逆、裏、対偶との関係
先ほど述べましたが、命題によっては真偽を判定したり、真であることを証明するのが難しい命題があります。
たとえば、「ある数が無理数である」ことの証明です。これは意外と難しい証明です。
無理数は、これが無理数だと言える数ではなく、単に有理数の定義にあてはまらない数だからです。
しかし、命題の対偶を利用すれば、かなり易しい証明になります。このように、真偽の判定や証明の難しい命題に対しては、逆、裏、対偶を利用して視点を変えることで、真偽の判定や証明が楽になることがあります。
初見の問題だけでなく、入試レベルの問題になると、様々な視点から問題を眺めることが必要になります。
この単元では、そのような視点を身に付ける訓練のつもりで取り組むと良いでしょう。また、主観的にならず、客観的な視点を養うためにも必要な単元かと思います。
命題の真偽と、その逆、裏、対偶の真偽は一致するか
命題「ｐ⇒ｑ」の真偽と、その逆、裏、対偶の真偽との関係を考えます。
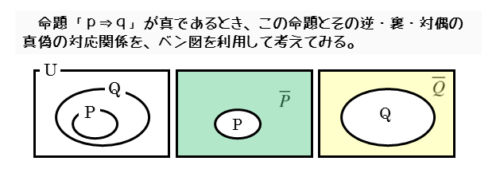
ある命題「ｐ⇒ｑ」が真であるとします。このとき、条件ｐ，ｑに対応する集合Ｐ，Ｑには、Ｐ⊂Ｑという包含関係があります。
ベン図を使いながら、命題が真であるときの逆、裏、対偶の真偽を調べてみましょう。
ベン図において、仮定ｐの否定は集合Ｐの補集合で、結論ｑの否定は集合Ｑの補集合です。
これらの包含関係を考えれば、命題の逆、裏、対偶の真偽を判定することができます。
命題の逆の真偽
命題「ｐ⇒ｑ」が真であるとき、その逆「ｑ⇒ｐ」の真偽を考えてみましょう。
ベン図から反例が存在するので、Ｑ⊂Ｐという包含関係が成り立ちません。
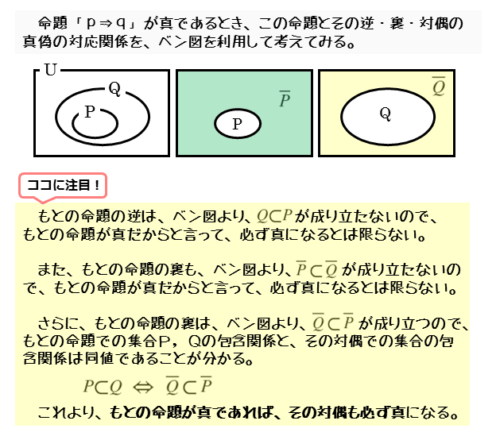
命題「ｐ⇒ｑ」が真であるからといって、その逆が必ず真になるとは限りません。
もとの命題が真であっても、その逆が真とは限らない。
命題の裏の真偽
命題「ｐ⇒ｑ」が真であるとき、その裏「ｐの否定⇒ｑの否定」の真偽を考えてみましょう。
Ｐの補集合とＱの補集合との包含関係をベン図を使って調べます。
ベン図から反例が存在するので、Ｐの補集合⊂Ｑの補集合という包含関係が成り立ちません。
命題「ｐ⇒ｑ」が真であるからといって、その裏が必ず真になるとは限りません。
もとの命題が真であっても、その裏が真とは限らない。
命題の対偶の真偽
命題「ｐ⇒ｑ」が真であるとき、その対偶「ｑの否定⇒ｐの否定」の真偽を考えてみましょう。
Ｐの補集合とＱの補集合との包含関係をベン図を使って調べます。
ベン図から、Ｑの補集合⊂Ｐの補集合という包含関係が成り立ちます。
命題「ｐ⇒ｑ」が真であるとき、その対偶は必ず真になります。
もとの命題が真であれば、その対偶も真。
このように、与えられた命題が真であれば、その対偶も必ず真になります。命題の真偽を判定し辛いとき、命題とその対偶の関係を利用します。
また、逆と裏は対偶の関係になるので、その真偽は一致します。ですから、命題とその逆、裏、対偶の真偽を調べるのは、実質、命題かその対偶のどちらかと、逆か裏のどちらかの２つの真偽を調べるだけで済みます。
命題とその逆、裏、対偶の関係を知っていれば、真偽を調べるのは実質２回で済む。
逆、裏、対偶の真偽だけでなく、もとの命題の真偽を調べる問題は、入試でも頻出です。ベン図を上手に利用して、素早く真偽を調べましょう。
次は、逆、裏、対偶を扱った問題を実際に解いてみましょう。